AnExtremelyLongName

32 base a converted to base 10 is 3a + 2

23 base b converted to base 10 is 2b + 3

3a + 2 = 2b + 3

3a = 2b + 1

Guessing and checking we can easily get a = 5, b = 7.

5 + 7 = 12

Hint: Use law of sines

In the old days it was possible to recieve up to 5 hearts from each person. But still that barely makes a difference as 111426 hearts is still a massive number to achieve regardless.

Confused, what is "\(-4"?

nvm deleted (wasn't an answer/explanation)

...

1. Type the problem out manually so we don't have to have the trouble of comprehending your picture

2. This is obviously your homework take your problems to Brainly or something.

I guess someone will answer regardless

case 1: there are 3 zeros.

 - This one is pretty trivial, we know there are 9 of these numbers (1000, 2000, 3000... 8000, 9000)

case 2: there are 2 zeroes.

 - All we need to do is find the number of such cases for the 1000s and multiply that for 9.

1001, 1002... 1008, 1009 there are 9 cases for which the the single digit is not zero

1010, 1020, ... 1080, 1090 there are 9 cases also.

Obviously there are also 9 cases for the non-zero hundreds digit cases.

So there are (9 + 9 + 9) * 9 = 243 for case 2.

So case 1 + case 2 = 252 such numbers, confirming guest's answer

thanks, I should probably find another forum XD

Graphing the possible values for $a>b$ as positive integers. (Selected Points are the possible values)

_____________________________________________________________

a is y-axis

b is x-axis

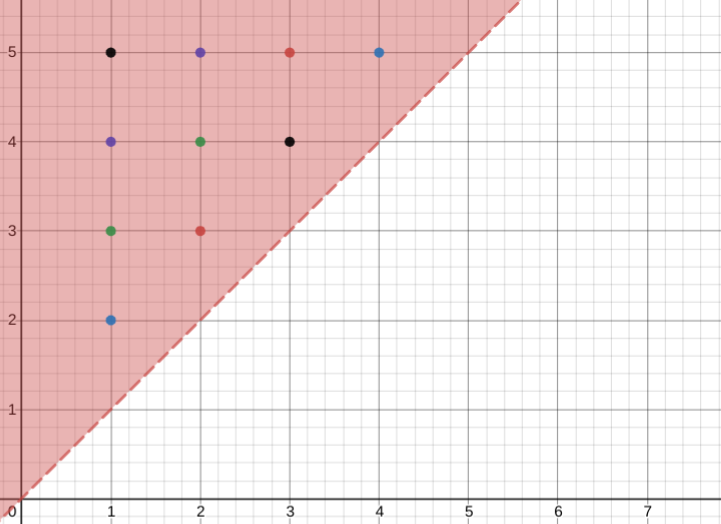
By plugging in values of A and B...

Notice how if we set b = 1, we can get an infinite series as $a$ increases by increments of 1.

Notice how if we set b = 2, we can get the same thing except the starting term is different.

So the answer really is the sum of an infinite series of infinite series'.... very interesting!

_____________________________________________________________

Let us find the infinite series if b = 1 and $a$ increases to start off:

$\frac{1}{20}+\frac{1}{40}+\frac{1}{80}...$

_____________________________________________________________

The formula for an infinite series is

$\frac{a_{(1)}}{1-r}$

_____________________________________________________________

So the series for b = 1 is $\frac{1}{10}$.

By applying the same method, we know that the series for b = 2, b = 3, b = 4 is:

1/100

1/1000

1/10000

respectively...

So now we have to find the sum to THAT infinite series, which is:

$\frac{\frac{1}{10}}{1-\frac{1}{10}} = \boxed{\text{math is fun}}$

*an interesting thing is as you add the number of different variables, the higher dimensions the graph is. Interesting how we don't need to actually VISUALIZE higher dimensional graphs, we can just calculate the sum if you have the method down.

Hint:

Set the length of the grey rectangle to X

Set the width of the grey rectangle to Y.

Use simple algebra to find the other rectangle's width and length in terms of X and Y.

Then solve an equation.

good job