Wait! There is another solution, as well! Heureka was so close to the second solution, too. I think the user forgot about taking the square root always results in a positive and negative answer. Anyway, I like Heureka's method, but here is my method of solving.
The original equation is \(\sqrt[3]{x^2-4x+4}=16\). Now let's solve for x:
| \(\sqrt[3]{x^2-4x+4}=16\) | Raise both sides of the equation to third power to eliminate the cube root. |
| \(x^2-2x+4=16^3\) | Do 16^3. luckily for us, we need not know the exact value of it yet. We can manipulate it in a base of 2 so we do not need to do a difficult calculation. |
| \(x^2-2x+4=16^3\) | Usually, you would subtract 16^3 on both sides , but \(x^2-2x+4\) happens to be a perfect-square trinomial, and transforming it into one is much easier computationally. |
| \((x-2)^2=16^3\) | Take the square root of both sides. Of course, when you take the square root of both sides, it results in a positive and a negative answer. |
| \(|x-2|=\sqrt{16^3}\) | Now, I will use power rules creatively to simplify 16^3. |
| \(|x-2|=\sqrt{(2^4)^3}\) | 2^4 is equal to 16, so I have not changed the right-hand side of the equation at all. Now, I will utilize another power rule that states that \((a^b)^c=a^{b*c}\) |
| \(|x-2|=\sqrt{2^{4*3}}=\sqrt{2^{12}}\) | When you are taking the square root of an even power, just divide the power by 2. Let me show you why. |
| \(\sqrt{a^{2k}}=\sqrt{(a^k)^2}=a^k\) | What I have shown here is that any number raised to the power of a number that is a multiple of 2 is simply halved when the square root is taken to it. |
| \(\sqrt{2^{12}}=\sqrt{(2^6)^2}=2^6\) | I have done the exact same process as above, just with the numbers that are given. |
| \(|x-2|=2^6\) | With absolute value expressions, the answer is divided into the positive and negative answer. Before we do that, however, we must evaluate 2^6. You may have memorized it, but I have a trick if you haven't. |
| \(2^6=(2^3)^2=8^2=64\) | Therefore, 2^6=64. |
| \(|x-2|=64\) | Now, let's solve for each equation separately. |
| \(x-2=64\) | \(-(x-2)=64\) | |
| \(x=66\) | \(x-2=-64\) | |
| \(x=-62\) | ||
Normally, with equations inside radicals, you would have to check both solutions, but here it isn't necessary. This is because after cubing both sides, you end up with a quadratic, and an answer from a quadratic is always right--assuming no arithmetic error was made when solving. Therefore, your solution set is:
\(x_1=-62\)
\(x_2=66\)
.Here's another method to prove condition ii (\(\overline{AC}\perp\overline{DB}\)). I will utilize a two-column proof:
| \(AD=CD\) \(AB=CB\) | Given |
| \(\overline{AD}\cong\overline{CD}\) \(\overline{AB}\cong\overline{CB}\) | Definition of congruent segments |
| Figure \(ABCD\) is a kite | Definition of a kite (If a quadrilateral has two unique pairs of sides that are congruent, then the figure is a kite) |
| \(\overline{AC}\perp\overline{DB}\) | Property of a kite (Diagonals of a kite are perpendicular) |
This question has been answered at least 3 times on this forum. 6/2(1+2) evaluates to 9. Since this question has been asked multiple times on this forum, I have redirected you to 3 different explanations on how to get the answer:
1) https://web2.0calc.com/questions/6-2-2-1#r2
Here's another method that works, too. Let's use the zero-product theorem. If haven't heard of the theorem, then you have probably used it before, unbeknown to you. With this theorem, we can make the following equation with the roots of \(\pm2\)
\((x+2)(x-2)=0\)
The zero-product theorem states that at least one (or both) factors must be equal to zero for the left-hand side to equal 0. I have made an equation that contains both of the desired roots. Since we know that this equation has the desired roots and \(x^2+b-10=0\) has the same desired roots, we can conclude that \((x+2)(x-2)=x^2+b-10\). Now, solve for b:
| \((x+2)(x-2)=x^2+b-10\) | Expand the multiplication of both binomials by realizing that \((a+b)(a-b)=a^2-b^2\) |
| \(x^2-4=x^2+b-10\) | Subtract x^2 from both sides of the equation. |
| \(-4=b-10\) | Add 10 to both sides. |
| \(6=b\) | |
This is simply another method of solving.
1)
When the question asks to solve for h in the equation of \(V=2\pi r^2h\), it means get h, alone, on one side of the equation. This only requires one step, in this case:
| \(V=2\pi r^2h\) | Divide by \(2\pi r^2\) on both sides of the equation. |
| \(h=\frac{V}{2\pi r^2}\) | We're done! h is by itself. |
The appropriate answer choice, therefore, is D
2) If the domain is only {2, 4, 7}, just plug them in the original equation of \(f(x)=x^2-5\).
| \(f(2)=2^2-5=-1\) | |
| \(f(4)=4^2-5=11\) | |
| \(f(7)=7^2-5=44\) | |
Now, find the answer choice that has all three of these in its domain. That would be D again.
Maxwong has the correct idea, but I think missed the criterion that states that the triangle must be acute. With this restriction, there are not as many possibilities.
Have you ever heard of the Pythagorean Theorem? You probably have. But have you heard of the Pythagorean Inequalities Theorem? Maybe you have and maybe you haven't. I think my textbook summarizes the concept nicely and in a way that is fairly straightforward:
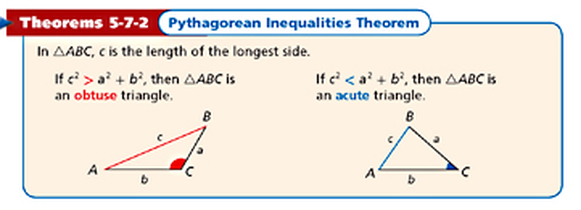
Source: http://abcpluspstudyguide.weebly.com/uploads/9/7/2/8/9728626/9817374.png?581
Of course, we seek triangles that only abide to acute triangles. We know 2 side lengths: 8 and 15. The remaining side I have labeled as s. Of course, there are 2 cases that are possible with s. Either it is the largest side or it is not. We will have to take both into account to solve this prolem:
For the first example, I will assume that s is the longest side, which corresponds to c in the picture above. Now, let's solve:
| \(c^2 | s is c. Whichever side you plug in for a and b does not matter. | ||
| \(s^2<8^2+15^2\) | Simplify the right hand side of the inequality to solve for s | ||
| \(s^2<64+225\) | |||
| \(s^2<289\) | Take the square root of both sides. | ||
| \(|s|<17\) | In an inequality, the absolute value has the following rule\(|a| . Now, let's apply it. | ||
| One inequality is already done. Divide both sides by -1 to get the other answer. Don't forget to flip the inequality sign! | ||
| We can clean up this solution by recognizing that we can represent the solutions as a compound inequality. | ||
| \(-17 | |||
Now, let's solve for s when is not the longest side:
| \(c^2 | This time, when we substitute, b will be in either a or b. | ||
| \(15^2 | Simplify both sides. | ||
| \(225 | SUbtract 64 on both sides. | ||
| \(161 | Take the square root of both sides. | ||
| \(\sqrt{161}<|s|\hspace{1mm}\text{or}\hspace{1mm}|s|>\sqrt{161}\) | The same logic applies for greater than symbols, too. In other words, \(|a|>b\rightarrow a>b\hspace{1mm}\text{and}\hspace{1mm} -a>b\) | ||
| Just like above, divide by -1 on the right inequality. | ||
| These inequalities cannot be combined into a compound inequality, unfortunately. | ||
The triangle must adhere to both conditions of \(-17 and ( \(s>\sqrt{161}\) or \(s<-\sqrt{161}\) )
Let's think about this logicall before our head explodes, though! If s is less than 17 and greater than √161, that means the following compound inequality arises:
\(\sqrt{161}
We don't care about the other inequality as it contains negative numbers, and negative numbers are nonsensical in the context of this problem, so I have excluded them. We aren't done yet! We have to figure out the first integer that is greater that 161. Well, \(\sqrt{161}\) is in between 12 and 13, so 13 is the first integer that is allowable under our given conditions.
Therefore, the only possible integer solutions are 13, 14, 15, and 16.
In the second question, Cphill interpreted it correctly, but if you meant \(R(x)=\frac{3x-3}{x^2-4}\) or \(R(x)=3x-\frac{3}{x^2-4}\), the answer is different. Let's think about what we have to do to figure out the vertical asymptote.
In both cases, we have rational fractions. Of course, we can't have a denominator of 0. This means that if we plug in a value for x that results in a denominator that equals 0, then it is officially outside of the domain. Let's figure out when x^2-4=0.
| \(x^2-4=0\) | You might notice that x^2-4 is a difference of 2 squares, but we don't need to take advantage of this, actually. This is because we have no b-term. Add4 to both sides. |
| \(x^2=4\) | Take the square root of both sides. |
| \(x=\pm2\) | |
This means that the vertical asymptote is at \(x=\pm2\), which corresponds to the answer choice of C.