ElectricPavlov

Simplify to 

x^2 + 31x + k        now complete the square for 'x'

(x+ 15.5)^2    - 240.25   + k       will have a double root at x = -15.5   when  k = 240.25 

Simplify to 

4x^2 -18x         Divide out '4'  so you can complete the square for 'x'

4 ( x^2 - 4.5x )         Now complete the square 

4 ( x- 2.25)^2   - 20 .25        Now you can see that p = - 20.25 

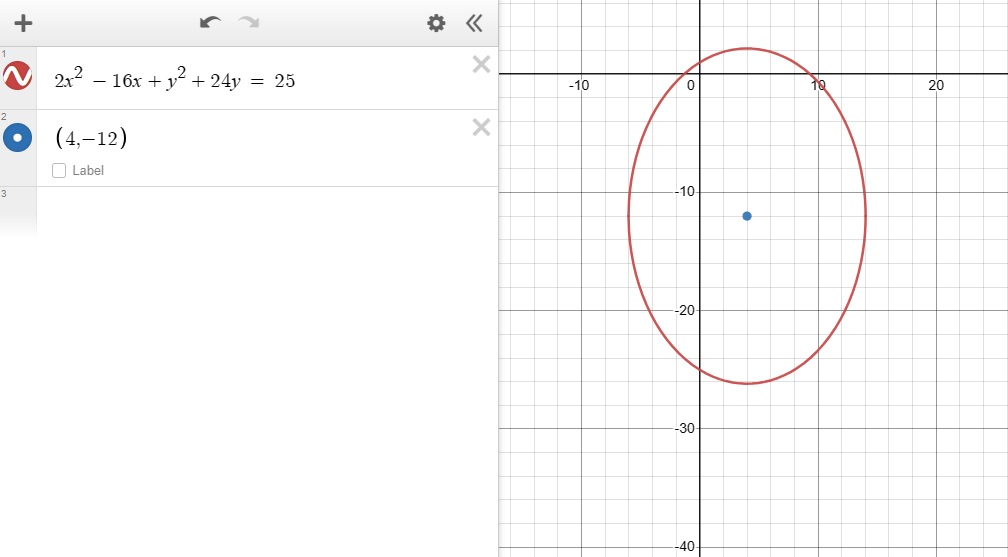
First, simplify to 

2 x^2 -16x      + y^2 + 24y    = 25         now complete the square for x and for y 

2 ( x-4)^2   -32       + (y+12)^2  - 144   =   25 

2 ( x-4)^2    +  (y+12)^2   = 201      re-arrange to standard ellipse form 

  (x-4)^2 / ( 201 / 2)    +    (y+12)^2 / 201   = 1         ( an ellipse centered at  4, -12  )

Now you can calculate the major and minor axes of the ellipse    as   sqrt ( 201/2)   and   sqrt (201)   

   then the area of an ellipse is given by      minor * major * pi   =   sqrt(201/2)  *  sqrt (201)  * pi   =    446.51 units^2

This means the quadratic is symmetric around the y - axis  and the roots are   - r   and + r 

soooo

(x-r)(x+r) = 0 

x^2 - r^2 = 0       from this you can see that the value of 'b'  has to be zero . 

See image 

Using ratios, 

'1' is to 'r'   as  sqrt(2) is to sqrt(2) + r ......or:

     1/r  = sqrt(2) / (r + sqrt(2) )     <======solve for 'r'   ..... cross multiply

    r + sqrt 2  = r sqrt 2 

    r - r sqrt 2 = - sqrt 2

     r ( 1 - sqrt 2)  = - sqrt2

     r =   sqrt (2) / ( sqrt2 -1) 

     r = 2 + sqrt 2     = 3.414 units 

Where are points  A   and  U  ?    DO you have the image? 

Two MORE ways to get the SAME answers that CPhill got :

One)

  x^2 -20x + 64   = 0      Factor (after a while you will be able to do this 'in your head' ....Really !)

 0 = (x - 4) ( x -16)          this shows  x = 4  or 16 

Two)

   x^2 -20x +64 = 0        Use Quadratic Formula    with   a = 1    b = -20     c = 64 

\(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\)

\(x = {-(-20) \pm \sqrt{(-20)^2-4(1)(64)} \over 2(1)}\)        Complete this calculation to find   x = 4 or 16        ..... as before ....

First simplify:

2ab - 12a + 3b - ab + 9a - 5b + _____ =

ab - 3a -2b        now it easier to see that this equals 

(a -2)(b - 3 )   IF  + 6 is included ....so:

2ab - 12a + 3b - ab + 9a - 5b +    6           

Recall the formula for the number of diagonals of a polygon

D= n * (n-3) /2       where n is the number of sides and D is the number of diagonals

So you have this: 

1/2 n = n * (n-3)/2        <==== solve for 'n'

1/2n = ( n^2 - 3n )/2      multiply through by 2

n = n^2 - 3n 

n^2 - 4n = 0 

n(n-4) = 0     shows n = 0  (throw out) or n = 4 sides     ( a quadrilateral.....square, rectangle etc)