Let's call a \(2 \times 2\) square a 'block' and a \(2 \times 1\) rectangle consisting of a column of two \(1 \times 1\) squares a 'blank'. So a \(2\times 10\) grid, for instance, consists of 10 consecutive blanks, numbered 1 to 10 from left to right, and a block occupies two consecutive blanks, say blanks 1 and 2, which I will denote by (1, 2). The max number of blocks that can be arranged on our \(2 \times 10\)grid is, of course 5, and the places they would occupy would be denoted as (1, 2), (3, 4), (5, 6), (7,8), and (9,10). We will first look at the number of arrangements on the \(2 \times 10\) grid and then extend the results to a \(2 \times 50\) grid.
First note that a block can occupy a \(2 \times k\) blan grid in k - 1 different ways. For instance, on a \(2 \times 10\) blank grid, the block can be placed on (1, 2), (2, 3), (3, 4), (4, 5), (5, 6), (6, 7), (7, 8), (8, 9), or (9, 10).
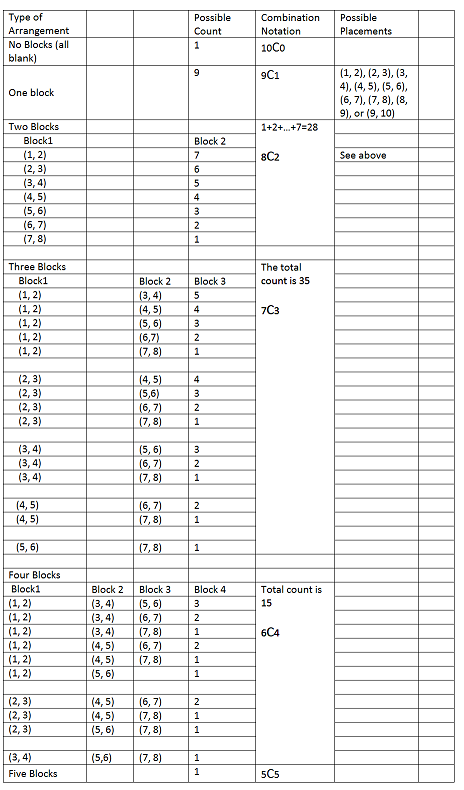
The following table shows that the number of arrangements for a \(2 \times 10\) grid is
\({10 \choose 0 } + {9\choose 1} +{8\choose 2}+{7\choose3}+{6\choose 4}+{5\choose5}=89\)
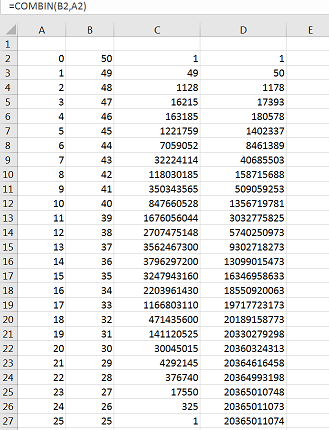
Thiscan be generalized to a \(2 \times 50 \) Grid. see below