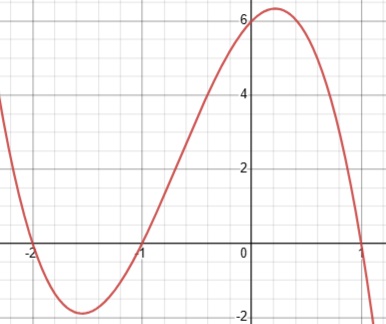
Usually, finding the x-intercepts of a cubic function is quite challenging, but some observation reveals we can use factoring to find the x-intercepts of this particular cubic function \(f(x) = -3x^3 - 6x^2 + 3x + 6\) by setting the function equal to 0 and then solving for the individual x-values.
\(-3x^3 - 6x^2 + 3x + 6 = 0 \\ -3(x^3 + 2x^2 -x - 2 = 0 \\ -3[x^2(x + 2) - 1(x + 2)] = 0 \\ -3(x^2 - 1)(x + 2) = 0 \\ -3(x - 1)(x + 1)(x + 2) = 0 \\ x=1 \text{ or } x = -1 \text{ or } x = -2\)
These x-values indicate the x-coordinate of the x-intercept. The y-coordinate of the x-intercept is always 0. Therefore, the x-intercepts are \((1, 0), (-1, 0), \text{ and } (-2, 0)\).
With this information of the x-intercept and the negative nature of the leading coefficient, you should be able to make a reasonably accurate graph of this cubic function, but below is one for reference.