AzizHusain

j(total energy that is radiated from the black body) = proportionality constant*black body's temperature(^4) 

cos45 degrees = sqrt(2) / 2.

76) y=-cubedrootx-2 +5

Domain: Notice that this function can take on any x value, so x can be all real numbers.

Range: The same goes for the y values, so y can be all real numbers as well.

78) y=-3sqrt4x-16

y = -3sqrt(4(x - 4)) -->

y = -3sqrt(4)sqrt(x - 4) -->

y = -3(2)sqrt(x - 4) -->

y = -6sqrt(x - 4).

82) sqrt8x-16=2sqrtx+2

x = 6.

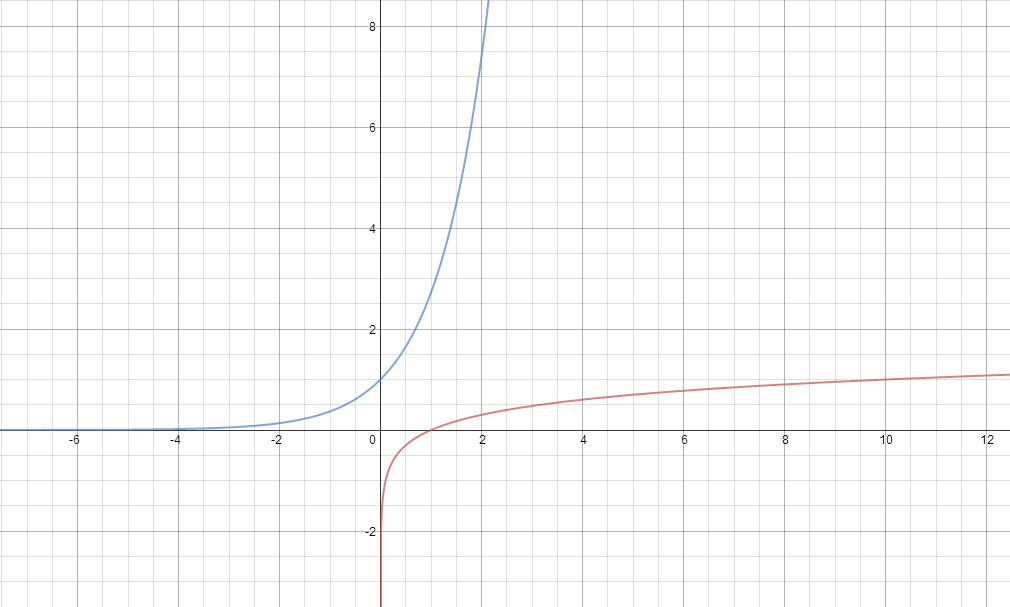
Logs are like exponentials except in a different form. We usually have problems like log(100), log base 2 of 32, etc. 

If there is no base written, then it is assumed to be log base 10. However, when we solve log problems, they are pretty much like exponentials, even when you compare the graphs [you will see that they are inverses of each other --- See graph at bottom of the post]. 

For example, log(100) = ? --> By using the properties of logs --> 10^? = 100 (We see exponential forms again!) --> 10^2 = 100, therefore log(100) = 2.

Now, if we have log base 2 of 32, what does it equal? By using properties of logs again --> 2^? = 32 --> 2^5 = 32, therefore log base 2 of 32 = 5.

What do we have to do with these radical functions? 

csc^-1(2)= 30 degrees or 0.523598775598.

cot^-1(-sqrt3)= -30 degrees or -0.523598775598.

f(x)=sqrtx+6 --> y = sqrtx + 6 --> Solve for x in terms of y -->

y - 6 = sqrtx -->

(y - 6)^2 = x --> Switch "x" and "y" --> y = (x - 6)^2.

f(x)=sqrtx-3 --> y = sqrtx - 3 --> Solve for x in terms of y -->

y + 3 = sqrtx -->

(y + 3)^2 = x --> Switch "x" and "y" --> y = (x + 3)^2.

x^2-16-x-4 = 0 

x^2 - x - 20 = 0 -->

(x - 5)(x + 4) = 0 -->

x = 5, -4.

x^2-16/x-4 = 0

(x + 4)(x - 4) / (x - 4) = 0 -->

(x + 4) = 0 -->

x = -4.

X^ means X to some exponent where X acts as the base. if X = 2, then we would have 2^ some power like 2^2 = 4, 2^3 = 8, or 2^0 = 1.

X^2+4 / (x-4) = 20 / (x-4) 

We know that x cannot equal 4 because the denominator will be undefined. x = 4 is the extraneous elimination, so we eliminate B and C.

Now, multiply both sides of the equation by (x-4) --> we end up with x^2 + 4 = 20 --> x^2 - 16 = 0 --> 

Difference of square --> (x + 4)(x - 4) = 0 --> x + 4 = 0 or x - 4 = 0 --> x = -4, 4

x = 4 is the extraneous solution, therefore, the only solution is x = -4, C.