Given:
AC is the diameter of a circle \(\omega\)
circle \(\omega\) has radius 1
D is a point on AC such that CD = 1/5
B is a point of circle \(\omega\) such that DB is perpendicular to AC
E is the midpoint of DB
Question:
AE = ?
I will assume that B is one the circumference of the circle, or else, it is not possible to find AE.
Using https://jspaint.app/#local:cf1101d801c0e, we can draw this figure:
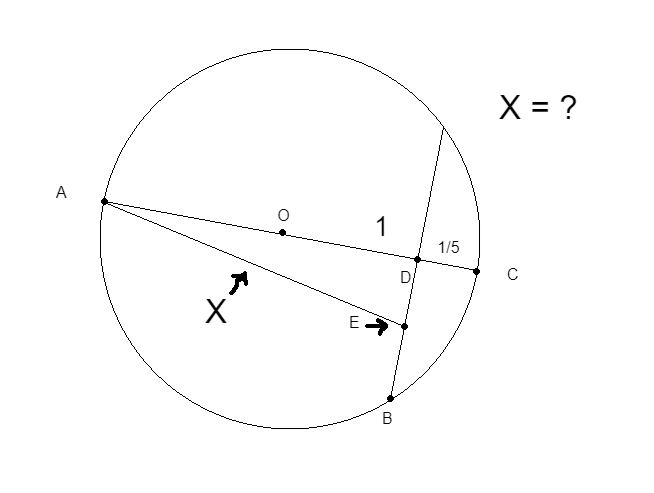
We can calculate length AE by doing AD^2 + ED^2.
We know that AD is 2 - 1/5 = 1 4/5, and squaring that gives us 3.24, so we get:
3.24 + ED^2 = AE^2
To calculate length ED, we first need to find length BD, which can be found by drawing a line OB, and then using the Pythagorean Theorem:
OD^2 + BD^2 = OB^2
We know that OD is 4/5 and OB is 1, so we can solve for BD:
0.8^2 + BD^2 = 1
0.64 + BD^2 = 1
BD^2 = 0.36
BD = square root of 0.36 or sqrt 36/100 = 6/10 = 0.6
BD = 0.6, so the midpoint divides BD into 2 equal segments, which as equal to 0.6/2 = 0.3, so ED = 0.3.
Using the Pythagorean Theorem to find AE, we get:
AD^2 + ED^2 = AE^2
1.8^2 + 0.3^2 = AE^2
3.24 + 0.09 + AE^2
AE^2 = 3.33
AE = square root of 3.33 or approximately 1.825.
The answer is \(\sqrt{3.33}\) or 1.825
Answer: \(\sqrt{3.33}\) or \(1.825\)
Okay we got the same answer.