EnchantedLava68

Repeating.  

While I have little experience with fractions within bases, the base converter calculator expressed 228/47 as 4.A2677AB8B29851339B5A574A2677AB8B29851339B5A574A0

With the proper highlights, we can find where it repeats

4.A2677AB8B29851339B5A574A2677AB8B29851339B5A574A2677AB8B29851339B5A574A2677AB8B29851339B5A57, and so on.  

Yeah, I know this was cheating, but at least it will help.  :)

The x-intercept occurs when y=0.  x-intercept is (6, 0)

The y-intercept occurs when x=0.  y-intercept is (0, -3)

Applying the distance formula/Pythagorean theorem, we have the distance between the points to be \(\sqrt{9+36}\), or \(\sqrt{45}\), equal to \({3}\sqrt{5}\)

No problem, most of the time was spent formating LaTeX and the picture anyways.  :)

1.  For this question, we are provided that each of the sides of the polygon is the same, and that it has 10 sides.  Because of this, the specified figure is a regular decagon, with angle measures of 144 degrees.  

To start, we go online and google regular decagon, to find a suitable image/graph (visualization is key).  This is the one I found:

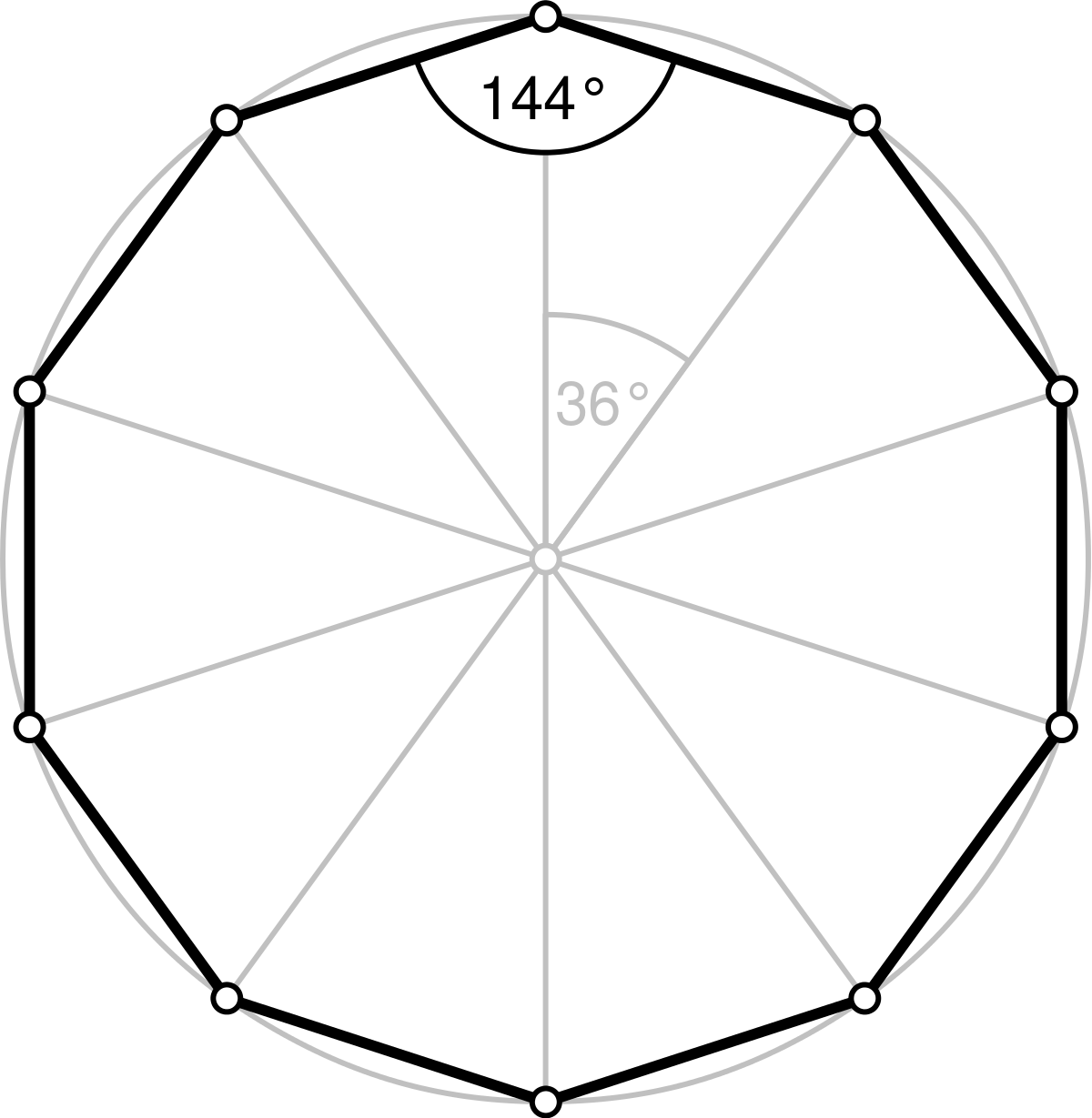
Let the topmost point be \(A_1\), and we label all points from \(A_1\) counterclockwise, getting \(A_4\) and \(A_8\).  Now, we connect \(A_1\), \(A_4\), and \(A_8\), forming an isoceles triangle.  Taking the Trapizoid \(A_1\)\(A_2\), \(A_3\), \(A_4\) into consideration, we draw the perpendicular from \(A_3\) to segment \(A_1 A_4.  \), point of intersection being X.  From this, we find that the angle \(A_3 A_4 X\) is 90 degrees, so the angle \(A_4 A_3 X\) has measure of 144-90, or 54 degrees.  

This means that angle \(A_3 A_4 X\) is 36 degrees, and that angle \(A_1, A_4 A_8\) is 90 degrees-36 degrees, or 54 degrees.  By the same reasoning, \(A_4 A_8 A_1\) is also 54 degrees.  This means that the angle measure of \(A_4 A_1 A_8\) is 180-54*2, or 180-108, 72 degrees.  Thus, to move point \(A_4\) to \(A_8\), we rotate around\( A_1\) by 72 degrees.  

Answer is 72 degrees.

2.  Unfortunately, I do not know how to do this question because I am very unfamiliar with dilations.  Good Luck though!.  

Because x and y > 0, x must be greater than y.  

We factor x^2-y^2=18 into

(x+y)(x-y)=18

Because x and y both must be positive integers, x+y and x-y are also both positive integers.  Using this, we also find that x+y >x-y

18 factors into 

1*18 -> x+y = 18, x-y = 1.  No integer solution

2*9 ->  x+y = 9, x-y = 2, No integer solution.  

3*6 -> x+y = 6, x-3 = 3, No integer solution.  

Thus, we find that there are no solutions.  

0 pairs total.  

A sense of direction is really important here, a graph is essential.  

Basically, we find that in total, he has walked directly northward \(3\sqrt{3}\) miles (you have to visualize/graph and 30-60-90 triangle), and directly eastward 6 miles (4+2).  

Using the Pythagorean theorem, the distance from the starting point would be the hypotenuse of a right triangle with legs \(3\sqrt{3}\) and 6, or\(\sqrt{{3\sqrt{3}}^2+6^2}\), simplifying to \(\sqrt{27+36}\),  \(\sqrt{63}\),  \(3\sqrt{7}\)

In short, the answer I got was 

 \(3\sqrt{7}\)

Because i is not real, -1 is real, 1 is real, and -i is not real, we have 

 f(i) + f(1) + f(-1) + f(-i)

= (i+2) +1 +1 +(-i+2)

= 2+1+1+2

=6

Google Translate lol

Convert to COD or COI

Mélanie does not save the essay.

Tony brings the skates in his hockey bag.

Do we have the answer?

You don't phone your parents.

First, we start by assuming that x < 2.  

Thus, it must satisfy the equation f(x) = 9x+16 = -2.  

9x+16= -2.  

9x = -18

x= -2.  

Because this is < 2, we know that x = -2 is a solution.  

Now for the second case, namely, x ≥ 2.  

8x-40 = -2

8x= 38

x= 4.75

Because 4.75 ≥ 2, this solution is also valid.  

From the above method, we can decide that the sum of the possible values of x are -2 + 4.75, or 2.75

F

It turns out, 5!-1 is not 719, but in fact 119.