hairyberry

A) 

After Bob spent \(\frac{1}{3}\)then spent 2/3 of 2/3, which is \(\frac{2}{3}*\frac{2}{3}=\frac{4}{9}\). \(1-\frac{4}{9}-\frac{1}{3}=\frac{2}{9}\). He had 2/9 left.

B)

Set the price of a cap as c, and so each pair of shorts is c+30.

Set the amount of money Bob has at the beginning as x.

We get the equation \(\frac{x}{3}=4c+5(c+30)\), after bob buys 4 caps and 5 pairs of shorts

Bob has already spend 1/3 of his money, so he only has 2/3 left, so spending 2/3 of 2/3 is \(\frac{2}{3}*\frac{2}{3}=\frac{4}{9}\).

So, \(\frac{4}{9}x=16c\). 

We get the system \(\begin{cases}\frac{x}{3}=4x+5(c+30)\\\frac{4}{9}x=16c\end{cases}\).

\(\begin{cases}x=12c+15(c+30)\\x=36c\end{cases}\)

\(36c=27c+450\)

\(9c=450\)

\(c=50\)

\(x=50*36=1800\).

So, Bob had 1800 dollars at the beginning.

If \({a}^{b}={a}^{c}\) then \(b=c\).

Following this logic then, for A) \(2y = 5\),  \(y=\frac{5}{2}\).

For B, \({9}^{3u+5}={3}^{6u+10}\) ,\(6u+10=8\), \(u=-\frac{1}{3}\).

For C, \({64}^{5x}={8}^{10x}\).\(4x-1=10x\), \(x=-\frac{1}{6}\).

A general good way to determine if a function is exponential is if it can be written as \(f(x)=a*{b}^{x}+k\), (Note x is not a constant!!) the function is an exponential function. This accounts for all stretches and shifts. Note: \(f(x)=a*{b}^{dx+e}+k\) is not needed, because this can always be transformed into the form I gave.

\(y={2}^{x}\) satisfies this.

\(y={x}^{2}\), does not satisfy this. (x must be in exponent).

\(y=\sqrt{x}\) or \(y={x}^{\frac{1}{2}}\) does not satisfy this.

\(y=\sqrt[3]{x}\) or \(y={x}^{\frac{1}{3}}\) does not satisfy this.

\(y=\frac{1}{x}\) or \(y={x}^{-1}\) does not satisfy this.

\(y=8x-4\) does not satisfy this.

Only A is correct.

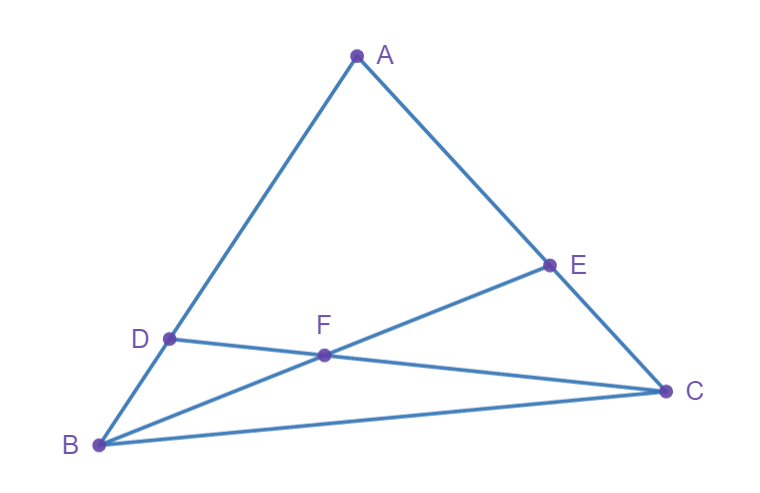
Great problem! I had to think some time about this one.

We first notice these are all cevian lines, so mass points work perfectly!

Becuase [BFC] = [FCE] then \(\overline{BF} = \overline{FE}\).

Similarly, \(\frac{\overline{DF}}{\overline{FC}}=\frac{3}{7}\).

Label the mass of D as 7, the mass of C as 3, so the mass of F is 3+7 = 10.

Because \(\overline{BF} = \overline{FE}\), then the mass is split evenly between B and E, so they are both 5.

The mass of D is 7, and the mass of B is 5, so the mass of A is 7-5 = 2.

Becuase mass of A * length of AD = mass of B * length of BD, we get that the ratio of the lengths of AD : BD is \(\frac{AD}{BD}=\frac{5}{2}\).

Similarly, \(\frac{AE}{EC}=\frac{3}{2}\). With these ratios, we also know the ratios of the area of some triangles, which we can use to our advantage.

Set the area of the shaded quadrilateral as x, and the area of the triangle ABC as Y.

We get two systems, by finding the area of triangle ADC and AEB, each two ways.

\(\begin{cases} \frac{3}{5}y=x+3 \\ \frac{5}{7}y=x+7 \end{cases}\). We solve and get x = 18. So the area of the shaded quadrilateral is 18.

Set the speed of the plane to k.

Set the distance to x.

A normal roundtrip is expressed as \(\frac{2x}{k}=\frac{10}{3}\), by the formula time = distance/speed.

A roundtrip with wind is \(\frac{x}{k+70}+\frac{x}{k-70}=\frac{23}{6}\), because the speed is 70 more when going to Jackson than when coming back.

To solve this system, \(\begin{cases}\frac{2x}{k}=\frac{10}{3} \\ \frac{x}{k+70}+\frac{x}{k-70}=\frac{23}{6} \end{cases}\). We want to solve for x, so we solve for k in terms of k. We should get \(k=\frac{3}{5}x\).

We plug this in, and solve. We get \(x=\frac{350\sqrt{69}}{9}\). So the distance is \(\frac{350\sqrt{69}}{9}\).

\(xy + x = \frac{3x + 2y + z + y + 2z}{3}\)

\(xy+x=\frac{3x+3y+3z}{3}\).

\(xy+x=x+y+z\)

\(xy=y+z\)

\(x=\frac{y+z}{y}\). Can also be written as: \(x=1+\frac{z}{y}\).

\(g(x)=f\left((x^2 - 2)/(x + 1)\right)\).

We can only input values from -8 to 8 in the function, so let's start from there.

\(-8\le\frac{{x}^{2}-2}{x+1}\le8\)

Consider there two seperately.

Case 1: \(-8\le\frac{{x}^{2}-2}{x+1}\)

\(\frac{{x}^{2}+8x+6}{x+1}\ge0\)

Use the method of intervals, or the wavy curve method. (I love that name ).

\({x}^{2}+8x+6\) has roots at \(-4 \pm \sqrt{10}\). 

so we get \(\frac{{x}^{2}+8x+6}{x+1}\ge0\) on the intervals \([-4-\sqrt{10}, -1)\cup[-4+\sqrt{10}, \infty)\). Remember, you can't plug -1 in so thats why it's not included.

Case 2: \(\frac{{x}^{2}-2}{x+1}\le8\). (I will spare some explanation here, its the same as above).

The interval turns out to be \((-\infty, 4-\sqrt{26}]\cup(1, 4+\sqrt{26}]\).

Now, we need to find the intersection of these intervals, since it satisfies both conditions.

We get \([-4-\sqrt{10}, 4-\sqrt{26}]\cup[-4+\sqrt{10}, 4+\sqrt{26}]\).

This interval has a width of 16. 

Adding \(2\pi\) to the degree will result in the same thing, since radius is not changing so another possible polar coordinate to express \((3, \frac{3\pi}{4})\) is \((3, \frac{11\pi}{4})\).

If we have a negative degree than, it essentially flips the side so:

\((-3, \frac{7\pi}{4})\) and \((-3, \frac{-\pi}{4})\) are all equal. These are our three.

Rewrite this arithmetic sequence as \(a_{1}, a_{1}+r, a_{1}+2r, \dots, a_{1}+10r, a_{1}+11r\), where a₁ is the first term, and r is the common difference.

\(a_{1} + a_{3} + a_{5} + a_{7} + a_{9} + a_{11}\) is now \(a_{1} + a_{1}+2r + a_{1}+4r + a_{1} + 6r + a_{1} + 8r + a_{1} + 10r\)

\(a_{2} + a_{4} + a_{6} + a_{8} + a_{10} + a_{12}\)is now \(a_{1} + r + a_{1} + 3r \dots+ a_{1} + 11r\)

Each term in the second one has one more r than the first one, so subtracting:

\(6r=0, r=0\).

Sub this back in to equation 1,

\(6a_{1}=0\)

\(a_{1}=0\).

We get this first term is zero. Note, since the common ratio is 0, this sequence is just twelve zeros, but it satisfies the conditions, and is the only sequence to do so.