This question took me over an hour to solve, but I can now share my findings with you! I am making the assumption that you meant triangles AXB and AXC in place of APB and APC. It is quite algebra-intensive. If this is not what you meant, then I wasted a long time of my day today :(
I created a diagram, and I added line segments and circles where I found necessary. I realize that the diagram is quite large and cluttered. Here it is below:
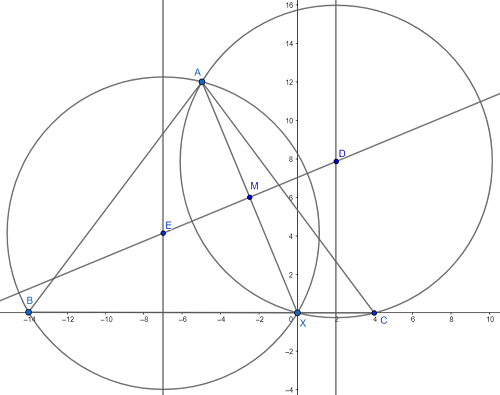
I will be utilizing coordinate geometry for this problem. With the diagram in its current orientation, I know that B=(-14,0) and X=(0,0) and C=(4,0). This way, I know the length of the base of \(\triangle ABC\) is 18. The only coordinate I need now is the y-coordinate of point A because that is the height of \(\triangle ABC\). Finding the area of the triangle is trivial at that point. Unfortunately, finding this coordinate is not so easy.
Since I don't know what the y-coordinate of point A, and I do not see an easy way to find the y-coordinate (or even the x-coordinate) of point A, I will denote them with variable letters. Let a = the x-coordinate of point A, and let b = the y-coordinate of point A. It would be nice if there was a way to relate a and b together, and I see one way of doing that. Since \(XA=13\), I can use the distance formula to relate a and b together like so:
\(d^2_{XA}=(a-0)^2+(b-0)^2\\ 13^2=a^2+b^2\\ b^2=169-a^2\\ b=\sqrt{169-a^2}\)
b is now written in terms of a, but now I am going to introduce a theorem that seems unrelated. That theorem states the following: The perpendicular bisector of a chord of a circle passes through the center of that circle. I have slyly used that theorem to my advantage here. \(\overline{AX}\) is a chord of both circumcircles of \(\triangle ABX\) and \(\triangle ACX\). \(\overleftrightarrow{ED}\) is the perpendicular bisector of \(\overline{AX}\), which, by the theorem I just stated, also pass through the circumcenters of both triangles.
We can find the slope of \(\overline{AX}\) and then use the properties of perpendicular line to find the slope of \(\overleftrightarrow{ED}\).
\(m_{\overline{AX}}=\frac{b}{a}\\ \therefore m_{\overleftrightarrow{ED}}=\frac{-a}{b}\)
But we can do more than that! Point M on the diagram represents the midpoint of \(\overline{AX}\), and we can find those coordinates in terms of a and b, too.
\(M=(\frac{a}{2},\frac{b}{2})\).
But we can do more that that, too. We can now derive an equation of \(\overleftrightarrow{ED}\) because we know the slope of the line and one point of the line. I will use point-slope form to start and simplify as much as possible from there.
| \(y-\frac{b}{2}=\frac{-a}{b}(x-\frac{a}{2})\\ y=\frac{-a}{b}x+\frac{a^2}{2b}+\frac{b}{2}\\ y=\frac{-2a}{2b}x+\frac{a^2}{2b}+\frac{b^2}{2b}\\ y=\frac{-2ax+a^2+b^2}{2b} \) | I substituted in \(169-a^2\) for \(b^2\) because I noticed that there would be some nice cancellation. |
| \(y=\frac{-2ax+a^2+(169-a^2)}{2b}\\ y=\frac{-2ax+169}{2b}\) | I decided not to simply further than this, at least for now. |
Remember that theorem I mentioned earlier? Yeah, we are using that one again. \(\overline{BX}\) is a chord of circle E, so E's center lies on its perpendicular bisector, which also lies on the line \(x=-7\). By parallel reasoning, circle D's center lies on \(x=2\). Let's use this newly discovered information to our advantage again!
| \(y_E=\frac{-2a*-7+169}{2b}\\ y_E=\frac{14a+169}{2b}\) | \(y_D=\frac{-2a*2+169}{2b}\\ y_D=\frac{-4a+169}{2b}\) |
We now know the x- and y-coordinates of the both circumcircles, so we can use the distance formula to write an expression for both radii.
| \(d_{\overline{EX}}=r_E\\ d_{\overline{EX}}=\sqrt{(-7-0)^2+(y_E-0)^2}\\ d_{\overline{EX}}=\sqrt{49+y^2_E} \) | \(d_\overline{DX}=r_D\\ d_\overline{DX}=\sqrt{(2-0)^2+(y_D-0)^2}\\ d_\overline{DX}=\sqrt{4+y^2_D}\) |
Conveniently, both radii are of the same length, so we can set the distances we just found equal to each other. We will finally be able to isolate a variable. How exciting! At this point, the rest is simply a test of your algebraic finesse. For an added challenge, I decided to avoid the use of a calculator.
| \(\sqrt{49+y^2_E}=\sqrt{4+y_D^2}\\ 49+y^2_E=4+y^2_D\\ 45+y^2_E=y^2_D\) | Let's subsitute in the corresponding expressions for \(y_E\) and \(y_D\). |
| \(45+\left(\frac{14a+169}{2b}\right)^2=\left(\frac{-4a+169}{2b}\right)^2\\ 45+\frac{196a^2+2*169*14a+169^2}{4b^2}=\frac{16a^2-2*169*4a+169^2}{4b^2}\\ 180b^2+196a^2+28*169*a+169^2=16a^2-8*169*a+169^2\\ 180(169-a^2)+196a^2+28*169*a=16a^2-8*169*a\\ 45(169-a^2)+49a^2+7*169*a=4a^2-2*169*a\\ 45*169-45a^2+45a^2+7*169*a=-2*169*a\\ 45*169+7*169*a=-2*169*a\\ 45+7a=-2a\\ -9a=45\\ a=-5\) | We finally solved for a. Yes, I checked if the value for a seems reasonable, and it certainly does. |
| \(b=\sqrt{169-a^2}\\ b=\sqrt{169-(-5)^2}\\ b=12\) | |
Finally! Remember that b was the y-coordinate of point A, which is also the height of \(\triangle ABC\). Now, we can finally find the area of the triangle.
\(A_{\triangle ABC}=\frac{1}{2}*18*12\\ A_{\triangle ABC}=108 \)
That's it! We are done.