TheXSquaredFactor

Max0815, you are very close; all you need to consider is the potential overlap. Look at the diagrams below.
 

I enjoyed it and I enjoyed it well.

It is amazing how all these hidden patterns can be extracted from a simple sequence of numbers formed in a triangular shape.  

This problem just requires some logic to crack it. 

Both numbers have 5 digits. A must be equal to or equal to or less than 2 because, otherwise, the result would exceed the 5-digit restriction. 4E is even, so A only has one value: 2. This leaves us with 2BCDE*4=EDCB2

4E must end in a 2. Only two values achieve this: 3 and 8. E cannot be 3 because 20000*4=80000. 8 is the only option then. This leaves us with 2BCD8*4=8DCB2

B2 must be a multiple of 4 because of the divisibility rules for 4. B cannot exceed 2 because 3000*4=12000. This would cause a carry for 2BCD8*4, and the result would be impossible. Only 1 works because that makes 8DCB2 end in a 12, which is divisible by 4. This leaves us with 21CD8*4=8DC12

4D+3 must end in a 1, so 7 and 1 are the only options. D cannot be 1 because all the digits must be unique, according to the original problem; therefore, d=7. This leaves us with 21C78*4=87C21

We have a carry of 3 from 4*7+3=31, and 4c+3 must result in a carry of 3 so that the result holds true. This leaves us with a basic algebra problem:

c=9

Therefore, \(21978*4=87912\)

Thank you for catching that \(1.1*0.9\neq 9.9\)

Constructing a diagram is a crucial step here; digesting all that information visually is extremely difficult without a visual aid. I have concocted one that I am proud of. I have tried to label everything in this diagram for your convenience. This problem most likely has many avenues toward achieving the correct answer, but I will present my approach for you:
 

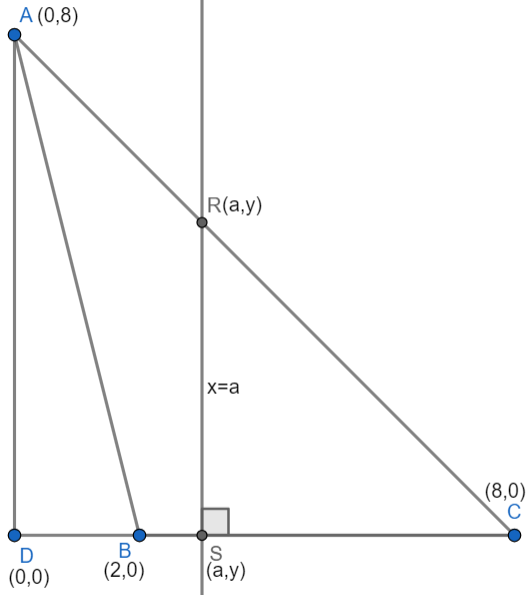
In the diagram above, I have added point D, which is the intersection of point A and point C. The point lies on the origin. Let's focus on some characteristics regarding \(\triangle ACD\) .

Point A and point D have the same x-coordinate, so a vertical segment connects them. Point C and point D share the same y-coordinate, so they must be connected with a horizontal segment. \(\overline{AD}\perp\overline{DC}\) because horizontal and vertical lines are always perpendicular; thus, \(m\angle ADC=90^{\circ}\).

\(AD=DC=8\), so \(\triangle ACD\) is also an isosceles triangle.

A triangle that is both right and isosceles is also known as a 45-45-90 triangle. It is possible to observe these similarities with \(\triangle RSC\).

\(\overline{AD}\parallel\overline{RS}\) because they are both vertical lines. Whenever a parallel line cuts through a triangle, the resulting triangles are similar. In this case, \(\triangle ADC\sim\triangle RSC\) . 

\(DC=8\) and \(DS=a\) , so \(CS=8-a\) . Because \(\triangle RSC\) is isosceles, \(RS=CS=8-a\) . The area of this triangle, according to the original problem, is 12.5. We know the lengths of the side lengths, so we can determine the value of a.

Yes, it is possible to solve for a here, and it is relatively simple from here on out. However, we can take a slight shortcut. The end goal is to determine the difference of x- and y-coordinates, but 8-a represents the height of the triangle. Since 8-a=5, we know that the y-coordinate is 5. 

 (3,5) is the coordinate of point R. \(|3-5|=2\)  is the positive difference.

Geometrists use diagrams in order to aid visualization. Although one could argue that this problem probably does not need the assistance of a diagram, I created one anyway. Here it is:

Our final goal is to express the relationship via a ratio. Calculating the area of a square is easier here.  

\(A_{\text{square}}=a^2\)

Let's consider what the area of a rectangle could be. The general formula for the area of a rectangle is \(A=lw\) .

\(\hspace{10mm}\textcolor{red}{l}=\textcolor{purple}{a}\textcolor{green}{+}\textcolor{blue}{10\%*a}=a+0.1a=1.1a\\ \textcolor{red}{\text{length}} \text{ is} \textcolor{blue}{\text{ 10 percent}} \textcolor{green}{\text{ more than}} \hspace{2mm}\textcolor{purple}{a} \)

\(\hspace{8mm}\textcolor{red}{w}=\textcolor{purple}{a}\textcolor{green}{-}\textcolor{blue}{10\%*a}=a-0.1a=0.9a\\ \textcolor{red}{\text{width}} \text{ is} \textcolor{blue}{\text{ 10 percent}} \textcolor{green}{\text{ less than}} \hspace{2mm}\textcolor{purple}{a}\)

Calculating the area of the rectangle is now possible:

\(A_{\text{rectangle}}=lw\\ A_{\text{rectangle}}=1.1a*0.9a\\ A_{\text{rectangle}}=0.99a^2\)

Let's now construct the ratio.

\(\frac{A_{\text{rectangle}}}{A_{\text{square}}}=\frac{0.99a^2}{a^2}=\frac{0.99}{1}=\frac{99}{100}\)

Since the fraction had to be a "common" fraction, the numerator and denominator had to be integral values. 

A standard deck of 52 cards comprises 13 cards of any particular suit. Although the problem never explicitly states whether or not replacement occurs, I will assume that there is no replacement. 

The problem is a compound event because there are two separate events that can satisfy the condition. They are the following:

• Drawing two hearts
• Drawing two diamonds

Calculating the probabilities of each event separately is probably the best way to undertake this problem. 

Of course, you could go through the above ordeal again; you could calculate the probability of the event of the first diamond and second diamond and then do the multiplication. However, you may be able to observe the parallelism. 13 diamonds are included in a 52-card deck. Drawing the first diamond and second diamond would, therefore, be probabilistically identical to drawing two hearts. This means that I already know the probability of drawing two diamonds: \(\frac{1}{17}\) .

The interior angle of a regular polygon can be determined with the following formula:

\(\frac{180(n-2)}{n}\) where n represents the number of sides the polygon has

The measure of each exterior angle of a regular polygon can be determined using the following formula:

\(\frac{360}{n}\) where n represents the number of sides the polygon has

According to the problem, "the measure of each interior angle is four times the measure of each exterior angle," so we can create an equation for this like the following:

This question requires some observation combined with knowledge of properties of parallelograms and triangle similarity.

Parallelograms, by definition, are quadrilaterals with opposite sides parallel. In this example, \(\overline{AD}\parallel \overline {FC}\) because of the previous statement. Because \(\overline{DF}\) intersects multiple segments, namely \(\overline{AD}\text{ and } \overline {FC}\), \(\overline{DF}\) is classified as a transversal. \(\angle ADF\text{ and }\angle F\) are a pair of angles known as alternate interior angles because they exist on opposite sides of the transversal while remaining on the "inner" side of the intersecting lines. Because \(\overline{AD}\parallel \overline {FC}\), the Alternate Interior Angles Theorem states that \(\angle ADF \cong \angle F\). \(\overline{AB}\) is another transversal bounded by parallel lines. Therefore, \(\angle A\cong \angle FBE\). Because there are two pairs of angles that are congruent in corresponding triangles, namely \(\angle ADF \cong \angle F\text{ and }\angle A\cong \angle FBE\), the Angle-Angle Similarity Theorem states that the triangles are similar. In this case, \(\angle AED\sim \triangle BEF\)

Even after all the logic above, I still do not any side lengths yet. There exists a constant of proportionality between similar triangles. Since the area of \(\triangle BEF\) requires an enlargement by a factor of 9 to obtain the area of \(\angle AED\), the constant of proportionality would be the square root of this. \(\sqrt{9}=3\). Therefore, each side length on the larger triangle is enlarged by a factor of 3. Because \(\overline{BF}\) and \(\overline{AD}\) are corresponding sides according to the triangle similarity statement and \(\overline{AD}\) is enlarged by 3, \(AD=3BF\). 

One property of parallelograms is that opposite side lengths are also congruent. Because \(BC=AD\text{ and }AD=3BF \), \(BC=3FC\). 

Using the principle of the Segment Addition Postulate \(FC=BF+BC=BF+3BF=4BF\). 

Since the constant of proportionality for \(\triangle BEF\text{ and }\triangle CDF\) is 4, the area of \(\triangle CDF\) is 16. 

16-1=15, which is the area of the quadrilateral \(BCDE\). 

\(A_{\text{ABCD}}=9+15=24\text{units}^2\)