Klar - wir schauen uns zunächst an, was in jedem Schritt dazukommt, und versuchen, das irgendwie in Abhängigkeit von n (Nummer des Folgenglieds) darzustellen.
Erstmal: Was kommt eigentlich dazu?
War vermutlich schon klar, aber hier haben wir's nochmal rot auf weiss. Nun stellt sich die Frage: Wie hängt das mit dem Index n zusammen?
Im Folgenden soll das erste Folgenglied a0 sein, also a0 = 2, a1 = 9 usw.
Ich unterteile mir jetzt den Zuwachs irgendwie, wie's mir intuitiv sinnvoll erscheint - nach Seiten nämlich. Ich hab auch das mal im Bild festgehalten:
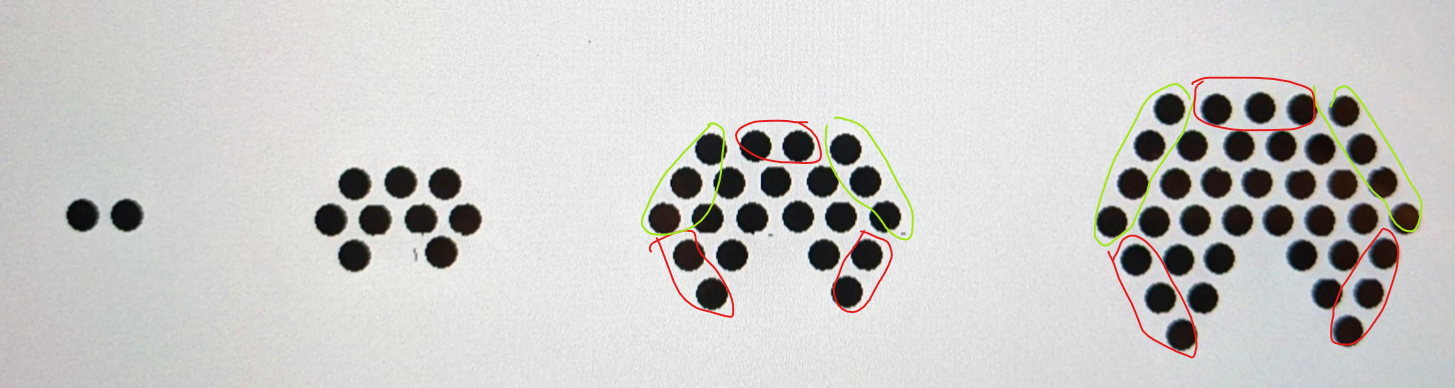
Man sieht: von a2 nach a3 wächst jede dieser Seiten um 1. (Auch in den vorherigen Schritten ist das so!) Außerdem erkennt man: Die grün markierten Seiten sind n+1 lang, die roten genau n. Im Vergleich zu an ist das Folgenglied an+1 also um 2(n+1) +3n größer.
Damit ergibt sich folgende Rekursionsformel:
an+1 = an +2(n+1)+3n
Aus dieser Formel ergibt sich auch eine explizite Formel für jedes Folgenglied: wir rechnen einfach ab n=0 jeden Zuwachs bis zu einem Index n zusammen!
Das sieht mit Summenschreibweise etwa so aus:
\(a_n = \sum_{k=0}^n ( 2(k+1)+3k) = \\ \sum_{k=0}^n (5k+2) = \\ \sum_{k=0}^n 5k + \sum_{k=0}^n 2 = \\ 5\cdot \sum_{k=0}^n k +2(n+1) =^* \\ 5 \cdot \frac{n(n+1)}{2} + 2(n+1) = \\ 2,5n^2+2,5n +2n +2 = \\ 2,5n^2+4,5n+2\)
Beim * habe ich die Gauß'sche Summenformel benutzt (gibts ausführlich bei Wikipedia falls du die noch nicht kennst).
Unsere explizite Formel ist also
an = 2,5n²+4,5n+2.
