textot

I don't know how you solved it, but the way I solved it directly proves that DX is the same value.

So here is what I did:

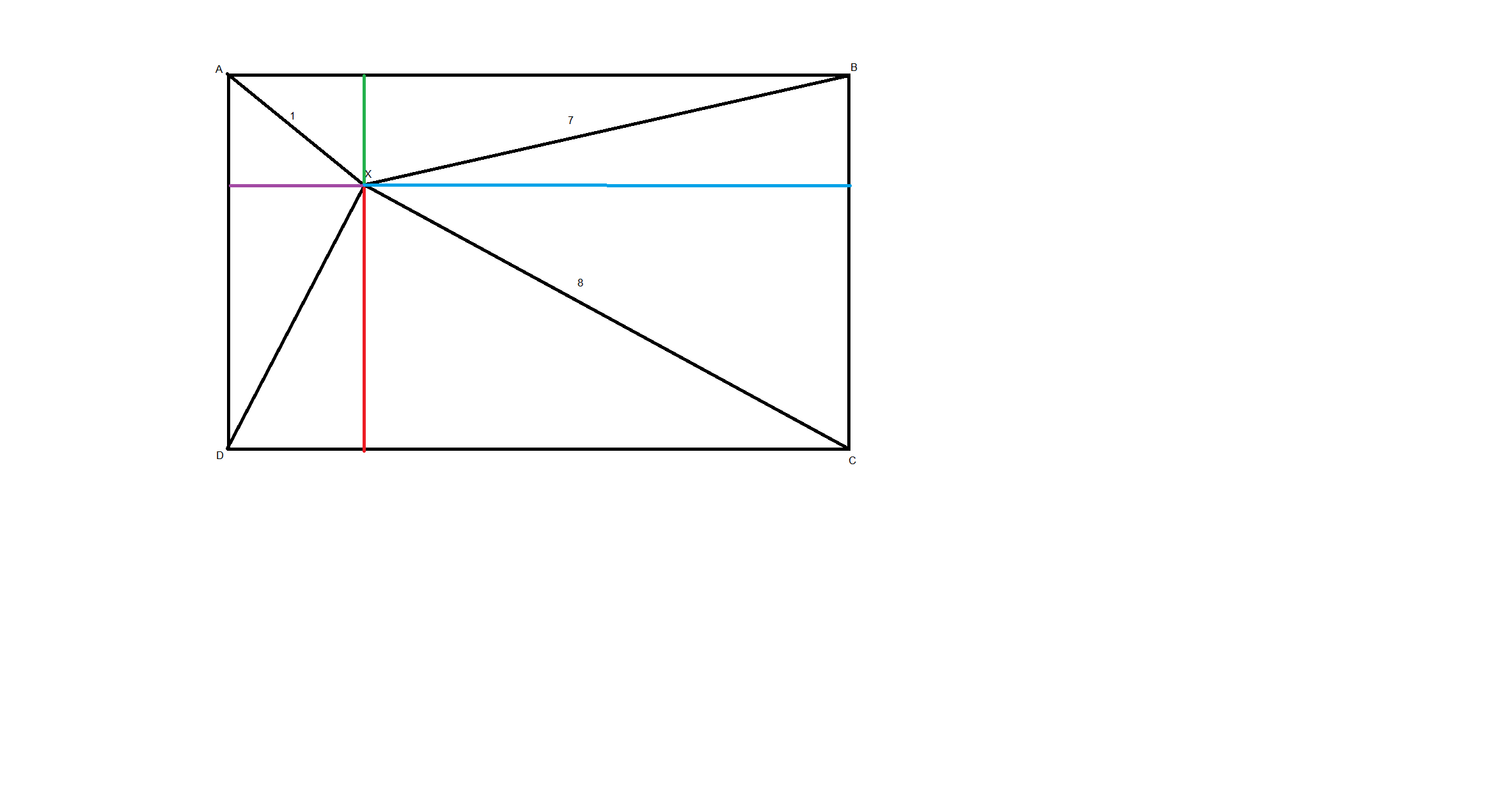
(the green, blue, red, and purple lines all intersect perpendicularly)

Let the green side be g, the blue side be b, the red side be r, and the purple side be p.

Then

 \(g^2+p^2=1\\ b^2+g^2=49\\ r^2+b^2=64\\\)

subtract the second equation from the first equation, then add the difference to the third equation to get

 \(DX=\sqrt{1-49+64}\\DX=4\)

For the second part of the question, suppose DX is not 4. The algebra above shows that it is 4, so it's a contradiction. 

(like mentioned before the way I solved it makes the proof self explanatory) 

The factors of 2008 in pairs are \((1, 2008), (2, 1004), (4, 502), (8, 251)\). The sum of the factors closest to each other will yield the smallest possible value for b, so the answer is \(8+251=\boxed{259}\)

The factored quadratic would look like this: \((x+8)(x+251)\)

JNK is similar to JML, so the ratio of their sides will be the same. Let JL = x. Then,

 \(\frac{7}{6} = \frac{x}{36}\\x=42\)

This is the same as asking to permute the string \(333221\) in distinguishable ways. That would be equal to \(6!=6\cdot5\cdot4\cdot3\cdot2\), but we're overcounting by a factor of \(3! = 3\cdot2\) multiplied by \(2!=2\), so we need to divide that from the original 6!. That would be equal to \(\frac{6\cdot5\cdot4\cdot3\cdot2}{3\cdot2\cdot2} = \boxed{60}\)

oops made a typo thanks for catching

Hint: the radius of the hemisphere is 2 times the radius of the sphere and the area of a sphere is \(\frac{4}{3}r^3\pi\), given radius r.

Then, just plug 2 in for r.

Can you take it from there?

10. To do that, find the surface area of 3 non-congruent rectangles, and then multiply by 2:

\(2(10\cdot4+10\cdot2+2\cdot4) = 136\)

11. To find the surface area of that, find the area of one of the 4 congruent triangles, multiply it by 4, and then add the area of the square:

\(\frac{6\cdot9}{2}\cdot4+6\cdot6=144\)

This might help: https://courses.lumenlearning.com/math4libarts/chapter/surface-area/#:~:text=The%20area%20of%20the%20net,of%20triangle%20A%20by%202.

r and s are both the roots of the polynomial \(ax^2+bx+c\), so r+s is just the sum of the 2 roots. According to Vieta's formulas, that is equal to \(\boxed{\frac{-b}{a}}\)

There are 2 cases: one case where the player who is fine either way is not in the two-person team, or another case where that player is.

For case 1, there are \(5\cdot4=20\) ways to select the teams, since there are 5 possibilities for a spiker and 4 for a setter.

For case 2, there are 9 ways to select the team, since the player who is fine either way can pair up with any of one of the 9 remaining people.

In total, there are \(20+9=\boxed{29}\) ways.

Or, you could factor:

\((x+5)(y+4)=1\)

When y = -4, the left-hand side will always equal zero, so \(\boxed{y=-4}\) is the solution.