One of the greatest ways to detect an error in solving is to do it yourself. I, too, have trouble spotting errors that others make--even if it is very obvious. However, if you do the problem and compare your answer with the given result, it is much easier to spot the error. I will also solve \(\frac{3}{x}+\frac{6}{x+3}=\frac{8}{x+1}\) because it is good practice.
| \(\frac{3}{x}+\frac{6}{x+3}=\frac{8}{x+1}\) | First, the solver in this problem states that the LCD is \(x(x+3)(x+1)\), which is correct. Now, let's multiply both sides by the LCD | ||
| \(\frac{3x(x+3)(x+1)}{x}+\frac{6x(x+3)(x+1)}{x+3}=\frac{8x(x+3)(x+1)}{x+1}\) | Simplify every fraction. Notice that, in every fraction, you can simplify it such that the fraction disappears. Let's do that. | ||
| \(3(x+3)(x+1)+6x(x+1)=8x(x+3)\) | Right away, I already see a disagreement between my answer and the solver's answer. They are both different. This is the error. Since I like going the extra mile of solving, I will do that! First, I'll distribute 3(x+3) first. | ||
| \((3x+9)(x+1)+6x(x+1)=8x(x+3)\) | You'll notice that it is not worth looking at the method that the solver uses, as I have already spotted the error. I can now use my own method to solve. Remember that \(ac+bc=(a+b)c\) by the inverse of the distributive property. I will use this in the next step. | ||
| \((6x+3x+9)(x+1)=8x(x+3)\) | Combine like terms in the first set of parentheses and subtract \(8x(x+3)\) from both sides of the equation. | ||
| \((9x+9)(x+1)=8x(x+3)\) | Unfortunately, I do not see a way to use the above reverse-distributive-property trick to simplify any further. I can factor out a 9 from both sides. | ||
| \(9(x+1)(x+1)=8x(x+3)\) | Now, do \((a+b)^2=a^2+2ab+b^2\). | ||
| \(9(x^2+2x+1)=8x(x+3)\) | Now, expand both sides. | ||
| \(9x^2+18x+9=8x^2+24x\) | Now, subtract 8x^2+24 from both sides. | ||
| \(x^2-6x+9=0\) | This trinomial happens to be a perfect-square trinomial. Let's use that to our advantage. | ||
| \((x-3)^2=0\) | Take the square root of both sides. Remember that taking the square root means taking the absolute value. | ||
| \(|x-3|=0\) | The absolute value splits your answer into the negative and positive answers. Luckily, the absolute value of 0 is always 0--whether positive or negative. | ||
| For the left equation, add 3. For the right equation, divide by -1. | ||
| For the second equation, we can stop because we already calculated the value for x when x-3=0. Of course, it's 3. | ||
This value for x is outside of the undefined singularity point, so this answer is correct.
For your information, you were solving this equation using the quadratic formula incorrectly. Your first line using the quadratic equation is \(x = {-6 \pm \sqrt{(-6)^2-4(1)(4)} \over 2(1)}\), but it should be \(x = {\textcolor{red}{-}(-6) \pm \sqrt{b^2-4ac} \over 2a}\). Also, \(-3\) happens to be an undefined singularity point because it is a solution to \(x+3=0\).
Another thing to mention is that I agree with Cphill that it is easier to simplify the left-hand side first, but it might be harder to detect the error if you do not do the problem as the solver did it.
Is the equation \(\sqrt{\sqrt{34}}=\sqrt{c^2}\) in which you want solved? This is what I intepret it as. I will solve it:
| \(\sqrt{\sqrt{34}}=\sqrt{c^2}\) | Square both sides of the equation to get rid of one set of square roots. |
| \(\sqrt{34}=c^2\) | Take the square root of both sides. Of course, taking the square root results in a positive and negative answer. |
| \(c=\pm\sqrt{\sqrt{34}}\) | Now, let's simplify. \(\sqrt{\sqrt{34}}\)Note that \(\sqrt[n]{a}=a^{\frac{1}{n}}\). |
| \(\sqrt{\sqrt{34}}=(\sqrt{34})^{\frac{1}{2}}\) | Let's use the same principle as above. |
| \((\sqrt{34})^{\frac{1}{2}}=\left(34^{\frac{1}{2}}\right)^{\frac{1}{2}}\) | In the current situation we are in, we will use the rule that \(\left(a^b\right)^c=a^{b*c}\). |
| \(\left(34^{\frac{1}{2}}\right)^{\frac{1}{2}}=34^{\frac{1}{2}*\frac{1}{2}}=34^{\frac{1}{4}}\) | Yet again, we will use the inverse of \(\sqrt[n]{a}=a^{\frac{1}{n}}\) to simplify. |
| \(c=\pm\sqrt[4]{34}\approx\pm2.4147\) | |
Now, we must check that \(\pm\sqrt[4]{34}\) are valid solutions to this equation. I'll check them separately.
| \(\sqrt{\sqrt{34}}=\sqrt{c^2}\) | Plug in the value of \(\sqrt[4]{34}\) and check its validity. |
| \(\sqrt{\sqrt{34}}=\sqrt{\left(\sqrt[4]{34}\right)^2}\) | This may look complicated, but it can be simplified by realizing that\(\sqrt{a^2}=a\), assuming \(a\geq0\) |
| \(\sqrt{\sqrt{34}}=\sqrt[4]{34}\) | We already calculated earlier than the square root of the square root of a number has a square root index of 4. |
| \(\sqrt[4]{34}=\sqrt[4]{34}\) | |
Now, let's check the other answer.
| \(\sqrt{\sqrt{34}}=\sqrt{\left(-\sqrt[4]{34}\right)^2}\) | This time, we cannot use the rule we used before because \(-\sqrt[4]{34}<0\). Let's rewrite this as an exponent. |
| \(\sqrt{\sqrt{34}}=\sqrt{\left(-34^{\frac{1}{4}}\right)^2}\) | Let's use the exponent rule we have used before that states that \(\left(a^b\right)^c=a^{b*c}\). Note that squaring a number automatically makes a number positive, so that is why the negative sign disappears in the next step. |
| \(\left(-34^{\frac{1}{4}}\right)^2=34^{\frac{1}{4}*\frac{2}{1}}=34^{\frac{2}{4}}=34^{\frac{1}{2}}=\sqrt{34}\) | Reinsert this into the equation and compare. |
| \(\sqrt{\sqrt{34}}=\sqrt{\sqrt{34}}\) | This statement is true, as both sides are the same, so both values for c are solutions. |
Therefore, \(c=\pm\sqrt[4]{34}\)
.There is a theorem that would be very helpful to know here. It is called the triangle exterior angle theorem. It states that the exterior angle is equal to the measure of the two remote (angle opposite the exterior) angles. This definition may be hard to understand, but a diagram would probably be useful. It may not be the neatest drawing, but you should understand the concept.
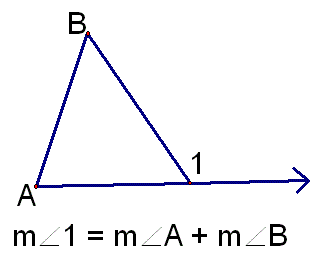
Now, let's use this to our advantage. Because of the triangle exterior angle theorem, we know that \(m\angle PAB=m\angle B+m\angle C\). Now that we have an equation that relates all the angles together, we can do the process of solving!
| \(m\angle PAB=m\angle B+m\angle C\) | We have already derived this equation. Now, substitute the values given for each angle. |
| \(x=90+mx+n\) | Now, substitute 1 for m, as given in the original description of the equation. |
| \(x=90+x+n\) | Subtract x from both sides. |
| \(0=90+n\) | Subtract 90 from both sides. |
| \(n=-90\) | |
Now, of course, we know that m=1 and n=-90. If you add those 2 values together, you get that \(m+n=1+(-90)=-89\)
.This diagram has a lot of information, and it can be somewhat difficult to decipher. With 2 radii, it should be possible to figure out the central angle. Before we start, we must understand arc length and its formula. The formula is below
\(\text{Arclength}=\frac{m^{\circ}}{360^{\circ}}*2\pi r\)
m = measure of the central angle, in degrees
r = radius of the circle
First, let's create 2 equations that demonstrate the relationship of r1 in this diagram:
| \(l=\frac{m^{\circ}}{360^{\circ}}*2\pi r\) | I am using "l" as my chosen variable for arc length. Of course, we already know the arc length; it is A, or 32. And we know that arc length corresponds with r1. |
| \(32=\frac{m^{\circ}}{360^{\circ}}*2\pi r_1\) | Great! Now, I will solve for r1 now. First, let's simplify the right hand side of the equation. |
| \(\frac{m^{\circ}}{360^{\circ}}*\frac{2\pi r_1}{1}\) | Multiply the fractions together. |
| \(\frac{2\pi r_1 m^{\circ}}{360^{\circ}}\) | The numerator and denominator have a GCF of 2, so factor that out. |
| \(\frac{\pi r_1 m^{\circ}}{180^{\circ}}\) | Reinsert this into the orginal equation. |
| \(32=\frac{\pi r_1 m^{\circ}}{180^{\circ}}\) | Multiply by 180 on both sides of the equation. |
| \(5760^{\circ}=\pi r_1 m^{\circ}\) | Divide by \(\pi m^{\circ}\) to isolate r1 |
| \(r_1=\frac{5760^{\circ}}{\pi m^{\circ}}\) | |
Let's do the exact same process for r2.
| \(34=\frac{m^{\circ}}{360^{\circ}}*2\pi r_2\) | We already from before what the right hand side simplifies to, so let's do that. |
| \(34=\frac{\pi r_2 m^{\circ}}{180^{\circ}}\) | Do the same process to solve for r2. Multiply both sides by 180. |
| \(6120^{\circ}=\pi r_2 m^{\circ}\) | Divide both sides by \(\pi m^{\circ}\). |
| \(r_2=\frac{6120^{\circ}}{\pi m^{\circ}}\) | |
We have two equations, and they are the following:
{
\(r_2=\frac{6120^{\circ}}{\pi m^{\circ}}\)
\(r_1=\frac{5760^{\circ}}{\pi m^{\circ}}\)
{
Now, let's subtract the 2 equations from each other. Let's see what happens. Unfortuntaely, I am no genius with LaTeX, so I could not line up the equal signs. Hopefully, you get the point...
\(\begin{eqnarray*} r_2=\frac{6120^{\circ}}{\pi m^{\circ}}\\ -\left(r_1=\frac{5760^{\circ}}{\pi m^{\circ}}\right)\\ \end{eqnarray*}\)
Let's subtract the two equations together. Let's start with the left hand side subtraction. \(r_2-r_1=1.5\), according to the given info. \(\frac{6120^{\circ}}{\pi m^{\circ}}-\frac{5760}{\pi m^{\circ}}=\frac{360}{\pi m^{\circ}}\). Knowing this, we can now solve for the central angle.
| \(1.5=\frac{360}{\pi m^{\circ}}\) | Multiply by \(\pi m^{\circ}\) on both sides. |
| \(1.5\pi m^{\circ}={360}\) | Divide by \(1.5\pi\) |
| \(m^{\circ}=\frac{360}{1.5\pi}\) | We can simplify the right hand side further, actually. First, let's convert 1.5 into a fraction. |
| \(\frac{360}{1.5\pi}=\frac{360}{\frac{3\pi}{2}}\) | In a fraction, \(\frac{a}{\frac{b}{c}}=\frac{a*c}{b}\). Let's apply it. |
| \(\frac{360}{\frac{3\pi}{2}}=\frac{360*2}{3\pi}\) | In the numerator and denominator, 3 can be factored out. |
| \(m^{\circ}=\frac{120*2}{\pi}=\frac{240}{\pi}\) | |
Now that I know the central angle in its exact form, I can now substitute it back into the arc length formula to ge the measure of the radii. Let's do that! FIrst, I'll solve for r1 first.
| \(l=\frac{m^{\circ}}{360^{\circ}}*2\pi r\) | As a reminder, this is the formula for arc length. Substitute the values we already know. |
| \(32=\frac{m^{\circ}}{360}*2\pi r_1\) | I have decided to leave out the measure of the angle for now, so the equation does not look like a monstrosity. Multiply both sides by 360. |
| \(11520=2\pi r_1m^{\circ}\) | Divide by 2 on both sides. |
| \(5760=\pi r_1m^{\circ}\) | Now, let's plug in m. |
| \(5760=\pi r_1\left(\frac{240}{\pi}\right)\) | Eliminate the pi's as they cancel out. |
| \(5760=240r_1\) | Divide by 240 on both sides. |
| \(r_1=\frac{5760}{240}=24units\) | I happen to know that 24^2=576, so this division was relatively easy for me. I will not forget the units, either! |
We don't have to do this same process for r2 luckily as \(r_1+1.5=r_2\). Therefore, \(r_2=24+1.5=25.5units\)
.