hectictar

If you were going to take statistics in college I would highly encourage you to take it in high school so that you would be more prepared for the college level class. But since you aren't going to college, then maybe don't take it.

(For me, statistics was pretty difficult in college. I think I found it so difficult because I never took it in high school. Whereas I found all my calculus classes not so difficult in college, and I do think that is in part due to the fact that I took calculus in high school. But of course I can't speak for everyone - I'm sure other people would find calculus much more difficult than statistics regardless of previous experience.) Tl;dr: College-level statistics is difficult for me, but that could be just be me.

Do you have to take a math class your senior year? What other options are there?

We put one open curly brace beside the "pieces" of the piecewise function, for example:

\(f(x)=\begin{cases} x+2 & \text{if}&x> 2 \\ x^2 &\text{if}& -3< x\leq 2 \\ 9 &\text{if}& x\leq-3 \end{cases}\)

This is the way to show the pieces of a piecewise function.

On the other hand, domains and ranges (and, of course, intervals) can be expressed in interval notation.

An interval is a set of values or numbers - not a set of expressions or functions.

E.g., the interval  [0, 5)  is every number between  0  and  5, including 0 and excluding 5.

And by looking at the graph for this function:

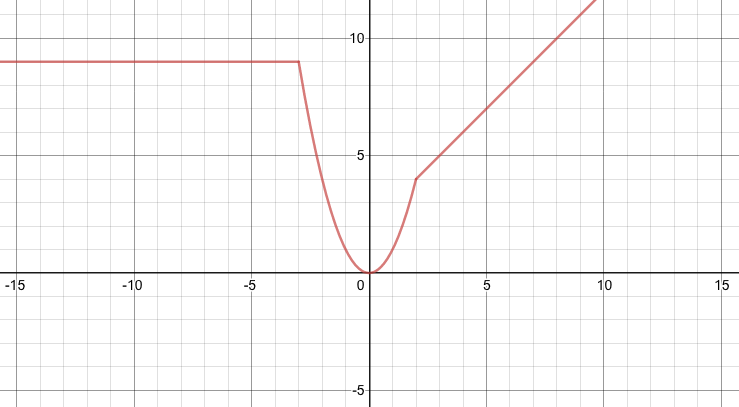
We can see:

All of those are intervals expressed in interval notation.

(At the points where  x = 2  and  x = -3 ,  the slope is undefined, and so the function is neither increasing nor decreasing, and so we do not include those values in the intervals of increase or decrease.)

Here is your image:

What is the question?

A good night sleep can help tremendously.

f(x)  =  x h(x)  =  13x + 1

By the transitive property of equality,

f(x)  =  13x + 1

g(x)  =  4 * f(x)

We multiply all the y-values by  4

Here is an example to maybe help you see why this is:

Let's let      \(f(x)=\sqrt{x}\)      and so      \(g(x)=4\sqrt{x}\)

Here is a table of points on the graph of  f(x)  and a graph to go with it:

And here is a table of points on the graph of  g(x)  and a graph to go with it:

Notice that all the y-coordinates of the graph of g(x) are 4 times that of f(x)

We can call this "a vertical strech by a factor of 4"

Here are the two graphs together:

Let the bigger number  =  a

And the smaller number  =  b

We know that

a + b  =  51

And we know that

a - b  =  7

Since we know that

a - b  =  7          , we can add  b  to both sides of the equation to conclude that

a  =  7 + b

Again, we know that

a + b  =  51          Now that we know  a  is equal to  7 + b ,  we can substitute  7 + b  in for  a

(7 + b) + b  =  51          And now we can solve this equation for  b

7 + b + b  =  51          One apple plus one apple equals two apples, so one b plus one b equals two b's

7 + 2b  =  51          Subtract  7  from both sides of the equation.

2b  =  44          Divide both sides by  2

b  =  22

And again, we know that

a  =  7 + b          Now that we know  b  is equal to  22 ,  we can substitute  22  in for  b

a  =  7 + 22

a  =  29

To recap:

a  =  29

b  =  22

We are given that  f(11)  =  34  so we know that  11  is in the domain.

domain so far  =  {11}

There exists an integer  11  such that  f(11) = 34 ,  so  f(34)  is defined. And so  34  is in the domain.

domain so far  =  {11, 34}

So notice that just like we had to add the result of  f(11)  to the domain, we will now have to add the result of  f(34)  to the domain (then the result of that, and the result of that, etc.).

Finally, we have reached a point where we do not have to add anything else to the domain.

4  is already in the set, so we do not have to add anything else.

So the smallest possible number of integers in the domain is  15

(Thank you CPhill for correcting my previous mistake!)