hectictar

3.

Let  P  be the point  (x, y)

So...

\(PA\ =\ \sqrt{(x-4)^2+(y+1)^2} \\~\\ PB\ =\ \sqrt{(x-6)^2+(y-2)^2} \\~\\ PC\ =\ \sqrt{(x+1)^2+(y-2)^2} \\~\\~\\ PA^2+PB^2+PC^2\ =\ (x-4)^2+(y+1)^2\ +\ (x-6)^2+(y-2)^2\ +\ (x+1)^2+(y-2)^2 \\~\\ PA^2+PB^2+PC^2\ =\ 3 x^2 - 18 x + 3 y^2 - 6 y + 62\\~\\ PA^2+PB^2+PC^2\ =\ 3( x^2 - 6 x + y^2 - 2 y) + 62\\~\\ PA^2+PB^2+PC^2\ =\ 3( x^2 - 6 x +9-9\ +\ y^2 - 2 y+1-1) + 62\\~\\ PA^2+PB^2+PC^2\ =\ 3( (x-3)^2-9\ +\ (y-1)^2-1) + 62\\~\\ PA^2+PB^2+PC^2\ =\ 3( (x-3)^2\ +\ (y-1)^2-10) + 62\\~\\ PA^2+PB^2+PC^2\ =\ 3( (x-3)^2\ +\ (y-1)^2)-30 + 62\\~\\ PA^2+PB^2+PC^2\ =\ 3( (x-3)^2\ +\ (y-1)^2)+32\)

So  X  must be the point  (3, 1)   and  k  must be  32

2.

Let  (x, y)  be the solution to the system. We know it is true that

y  =  (3x + 15) / 4

We also know it is true that:

x²  +  y²   =   36

                                                          Since   y  =  \(\frac{3x+15}{4}\)  we can substitute  \(\frac{3x+15}{4}\)  in for  y

x²  +  \((\frac{3x+15}{4})^2\)   =   36

x²  +  \((\frac{3x+15}{4})(\frac{3x+15}{4})\)   =   36

x²  +  \(\frac{9x^2+90x+225}{16}\)   =   36

                                                          Multiply through by  16  to eliminate the denominator

16x²  +  9x² + 90x + 225   =   576

                                                          Combine like terms

25x²  +  90x  +  225   =   576

                                                          Subtract  576  from both sides of the equation

25x²  +  90x  -  351   =   0

                                                         We can use the quadratic formula to solve for  x

x   =  \(\dfrac{-9\pm12\sqrt3}{5}\)

We can use the equation  y  =  (3x + 15) / 4   to find the y-coordinates of the intersection points.

When   x  =  \(\frac{-9\ +\ 12\sqrt3}{5}\)   ,   y  =  \(\frac14\cdot(\ 3(\ \frac{-9\ +\ 12\sqrt3}{5}\ )+15\ )\ =\ \frac{12\ +\ 9\sqrt3}{5}\)

When   x  =  \(\frac{-9\ -\ 12\sqrt3}{5}\)   ,   y  =  \(\frac14\cdot(\ 3(\ \frac{-9\ -\ 12\sqrt3}{5}\ )+15\ )\ =\ \frac{12\ -\ 9\sqrt3}{5}\)

So the intersection points are:

\(\big(\frac{-9\ +\ 12\sqrt3}{5},\ \frac{12\ +\ 9\sqrt3}{5}\big)\)     and     \(\big(\frac{-9\ -\ 12\sqrt3}{5},\ \frac{12\ -\ 9\sqrt3}{5}\big)\)

1.

P  is a point on the line   y = x   and   Q  is a point on the line  y = 7x.

So we can say...

Let  P  be the point  (a, a)           where  a > 0

Let  Q  be the point  (b, 7b)        where  b > 0

And  O  is the point  (0, 0)

Now we can make this equation:

the distance between  O  and  P   =   the distance between  O  and  Q

√[ a² + a² ]   =   √[ b² + (7b)² ]

                                                    Square both sides of the equation

a² + a²   =   b² + (7b)²

a² + a²   =   b² + 49b²

                                                    Combine like terms

2a²   =   50b²

                                                    Divide both sides by  2

a²   =   25b²

                                                    Take the positive square root of both sides

a   =   5b

the slope of  PQ   =   the slope between the points  (a, a)  and  (b, 7b)

the slope of  PQ   =   \(\dfrac{a-7b}{a-b}\)

                                                         Substitute  5b  in for  a

the slope of  PQ   =   \(\dfrac{5b-7b}{5b-b}\)

                                                         Combine like terms

the slope of  PQ   =   \(\dfrac{-2b}{4b}\)

                                                         Reduce the fraction by  2b

the slope of  PQ   =   \(-\dfrac{1}{2}\)

Using trig we can make this triangle:

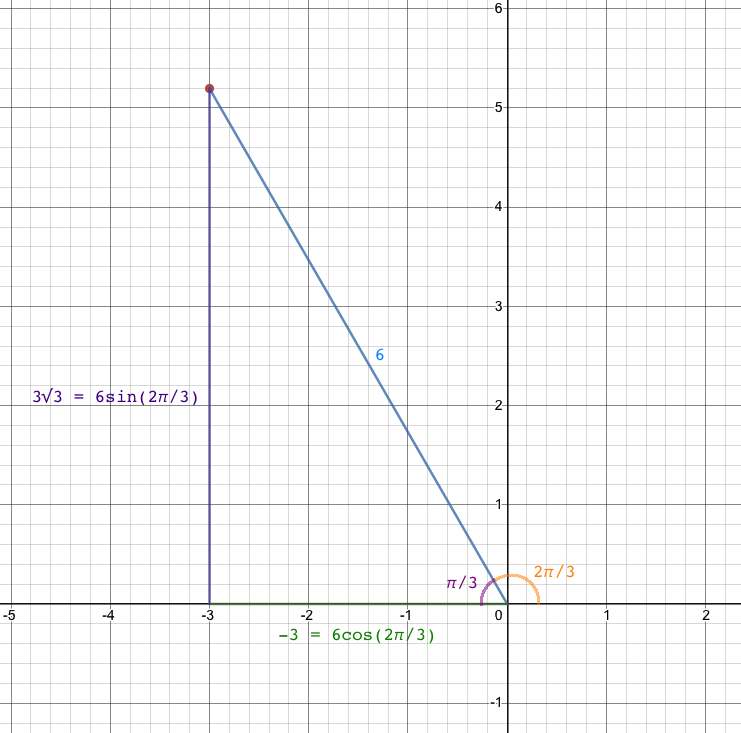
z  =  -3  +  3√3 i

                                                              Substitute   6 cos( 2π/3 )   in for   -3   and   6 sin( 2π/3 )   in for   3√3

z   =   6 cos( 2π/3 )  +  6 sin( 2π/3 ) i

                                                              Move the  i  to the front of the term

z   =   6 cos( 2π/3 )  +  6 i sin( 2π/3 )

                                                              Factor  6  out of both terms

z   =   6 [ cos( 2π/3 )  +  i sin( 2π/3 ) ]

\(G\ =\ \log \left( \dfrac{1 + \dfrac{3x + x^3}{1 + 3x^2}}{1 - \dfrac{3x + x^3}{1 + 3x^2}} \right)\\~\\~\\ G\ =\ \log \left( \dfrac{\dfrac{1+3x^2}{1+3x^2} + \dfrac{3x + x^3}{1 + 3x^2}}{\dfrac{1+3x^2}{1+3x^2} - \dfrac{3x + x^3}{1 + 3x^2}} \right)\\~\\~\\ G\ =\ \log \left( \dfrac{\dfrac{x^3+3x^2+3x+1}{1+3x^2} }{\dfrac{-x^3+3x^2-3x+1}{1+3x^2} } \right)\\~\\~\\ G\ =\ \log \left( \dfrac{x^3+3x^2+3x+1 }{-x^3+3x^2-3x+1 } \right)\\~\\~\\ G\ =\ \log \left( \dfrac{(1+x)^3 }{(1-x)^3 } \right)\\~\\~\\ G\ =\ \log \left( \left( \dfrac{1+x }{1-x } \right)^3 \right)\\~\\~\\ G\ =\ 3 \log \left( \dfrac{1+x }{1-x } \right)\\~\\~\\ G\ =\ 3 F \)  .

m∠ACD   =   m∠BCD  -  m∠BCA

Since a tangent line forms a right angle with a line drawn from the center of the circle to the point of tangency:

m∠BCD   =   90°

Note that △ABC is an isosceles triangle because  BC  is the same length as  BA.

And so the base angles,  ∠BCA  and  ∠BAC ,  have the same measure.

Since the sum of the interior angles of a triangle is  180°:

m∠ABC  +  m∠BCA  +  m∠BAC   =   180°

                                                                    We can substitute  168°  in for  m∠ABC  since  m∠ABC  =  168°

168°  +  m∠BCA  +  m∠BAC   =   180°

                                                                    We can substitute  m∠BCA  in for  m∠BAC  since  m∠BAC  =  m∠BCA

168°  +  m∠BCA  +  m∠BCA   =   180°

                                                                    Subtract  168°  from both sides of the equation.

m∠BCA  +  m∠BCA   =   180°  -  168°

                                                                    Combine like terms.

2 * m∠BCA   =   180°  -  168°

                                                      Divide both sides of the equation by  2

m∠BCA   =   (180° - 168°) / 2

                                                      Simplify.

m∠BCA   =   6°

Now we can go back to the original equation and plug in the information we know:

m∠ACD   =   m∠BCD  -  m∠BCA

m∠ACD   =   90°  -  6°

m∠ACD   =   84°

lateral area of cylinder with original radius   =   2π r h

lateral area of cylinder with doubled radius   =   2π (2r) h

lateral area of cylinder with doubled radius   =   2( 2π r h )

lateral area of cylinder with doubled radius   =   2( lateral area of cylinder with original radius )

The lateral area of the cylinder with the doubled radius is two times the lateral area of the original cylinder.

So...doubling the radius doubles the lateral area.

----------

surface area of cylinder with original radius   =   2π r h  +  2 π r²

surface area of cylinder with doubled radius   =   2π (2r) h  +  2 π ( 2r )²

surface area of cylinder with doubled radius   =   2π (2r) h  +  2 π  4 r²

surface area of cylinder with doubled radius   =   2( 2π r h )  +  4( 2 π r²  )

This one is a little trickier. Doubling the radius doubles the lateral area, but it quadruples the area of each base. And the surface area is the sum of the lateral area and the area of the bases.

I'm not sure if this is exactly what you want, but I hope it helps

The graph of f(x)=cosx [does not pass the horizontal line test] . Therefore, a domain restriction must be placed on the function for the inverse function to be defined. The domain restriction placed on f(x)=cosx  is [          [0, pi]             ] so that its inverse function is defined.

When the equation is in this form ( where the coefficient of  y  is  1 ),

we can pick off the slope of the line as the coefficient of  x .

Here, the coefficient of  x  is  \(\frac32\)   so

slope of line  m   =   \(\frac32\)

And...

slope of line perpendicular to  m  =  the negative reciprocal of  \(\frac32\)

slope of line perpendicular to  m  =  \(-\frac23\)

The equations that have  \(-\frac23\)  (or something equaivalent to  \(-\frac23\) ) as the coefficient of  x  represent lines perpendicular to  m