hectictar

area of triangle  =  (1/2) * ( base ) * ( height )

area of triangle  =  (1/2) * ( 4 cm ) * ( 3 cm )

area of triangle  =  6 cm²

Correction:

The possible outcomes are:

1, 5

2, 4

3, 3

4, 2

5, 1

And of these 5 possible outcomes, there is 1 where the number three appears at least once.

So the probability that the number three appeared at least once  =  1/5

(Thank you Alan)

The possible outcomes are:

a  1  and a  5

a  2  and a  4

a  3  and a  3

Of these 3 possible outcomes, there is 1 where the number three appears at least once.

And so the probability that the number three appeared at least once  =  1/3

Assuming  f(x) = ax² + bx + c,

f(0)  =  a(0²) + b(0) + c  =  c     and so   c  =  0

f(1)  =  a(1²) + b(1) + c  =  a + b + c  =  a + b + 0  =  a + b     and so   a + b  =  2

f(2)  =  a(2²) + b(2) + c  =  4a + 2b + c  =  4a + 2b + 0  =  4a + 2b     and so     4a + 2b  =  9

Now since  a + b = 2  ,  we can subtract  b  from both sides to get   a = 2 - b

Now we can substitute  2 - b  in for  a  into the equation  4a + 2b = 9  to get:

4(2 - b) + 2b  =  9          distribute  4  to both terms in parenthesees

8 - 4b + 2b  =  9          combine like terms

8 - 2b  =  9          subtract  8  from both sides of the equation

-2b  =  1          divide both sides of the equation by  -2

b  =  -1/2

Now we can substitute  -1/2  in for  b  into the equation  a + b = 2  to get:

a + b  =  2

a - 1/2  =  2

a  =  2 + 1/2

a  =  5/2

And so  f(x)  =  \(\frac52\)x²  - \(\frac12\)x  +  0

Now to find  f(3) ,  plug in  3  for  x  into the function.

f(3)  =  \(\frac52\)(3)²  - \(\frac12\)(3)  +  0   =   \(\frac{45}2\)  -  \(\frac32\)   =   \(\frac{42}{2}\)   =   21

Totally wasn't thinking about using a graph for this...that makes so much more sense!

number of 1x1 squares that contain the black square  =  1

number of 2x2 squares that contain the black square  =  4

number of 3x3 squares that contain the black square  =  4

number of 4x4 squares that contain the black square  =  4

number of 5x5 squares that contain the black square  =  1

I counted a total of  14  squares that contain the black square.

I think  \(y=\sqrt[3]{x}\)  is not neither.

\(f(x)=\sqrt[3]{x}\\~\\ f(-x)\ =\ \sqrt[3]{-x}\ =\ \sqrt[3]{-1\cdot x}\ =\ \sqrt[3]{-1}\cdot\sqrt[3]{x}\ =\ -1\cdot\sqrt[3]{x}\ =\ -\sqrt[3]{x}\ =\ -f(x)\)

(It is a little confusing because when I check that in WolframAlpha, it only agrees when it uses the "real-valued root")

Otherwise I agree with your answers

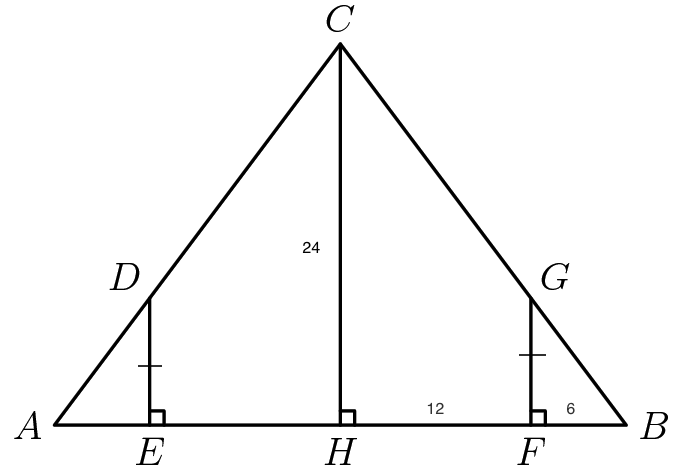
By AA similarity, △GFB is similar to △CHB, just as you said 

This means we can make the following equation:

GF / FB  =  CH / HB

                                      Now we can substitute  6  for  FB,  24 for  CH,  and  18  for HB

GF / 6   =   24 / 18

                                      Multiply both sides of the equation by  6

GF   =   (24 / 18)  *  6

                                      Simplify the right side of the equation

GF   =   8

Now we can find the area of  △GFB

area of △GFB   =   (1/2) * FB * GF   =   (1/2) * 6 * 8   =   24

We can see that because the left side of the big triangle is symmetrical to the right side, △GFB is congruent to  △DEA. (We can also say that since  m∠GBF = m∠DAE,    m∠GFB = m∠DEA,   and  DE = GF,  by AAS,  △GFB ≅  △DEA)

This means the area of △DEA is also 24 sq cm

Now we can find the area of △ABC.

area of △ABC  =  (1/2) * AB * CH  =  (1/2) * (2 * 18) * (24)  =  432

Now we can find the area of CDEFG.

area of CDEFG   =   area of △ABC  -  area of △GFB  -  area of △DEA

area of CDEFG   =   432  -  24  -  24

area of CDEFG   =   384   (and that is in sq cm)

area of figure   =   area of blue rectangle  minus  area of purple triangles

area of figure, in sq. in.   =   21 * 20    -    2 * 1/2 * (21 - 16) * (20 - 9) * 1/2

area of figure, in sq. in.   =   392.5

75%  of  b  is  12

We can replace  " % "  with  " /100 ",  " of "  with  " * ",  and  "is"  with  " = "

75/100 * b  =  12

Now we have to solve the above equation for  b  . Let's multiply both sides of the equation by  100/75

b  =  12 * 100/75

b  =  1200/75

b  =  16