Für 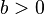 ist
ist  . Für
. Für  ist
ist  nicht definiert.
nicht definiert.
Per Definition gilt  , für
, für  . Der Ausdruck
. Der Ausdruck  wird entweder undefiniert gelassen oder – sofern dies zweckmäßiger ist – als 1 definiert. Siehe Potenz.
wird entweder undefiniert gelassen oder – sofern dies zweckmäßiger ist – als 1 definiert. Siehe Potenz.
$${\sqrt{{\sqrt{{\mathtt{a}}}}}} = {\sqrt[{{\mathtt{{\mathtt{4}}}}}]{{\mathtt{a}}}}$$
$${\sqrt[{{\mathtt{{\mathtt{4}}}}}]{{\sqrt[{{\mathtt{{\mathtt{3}}}}}]{{\mathtt{b}}}}}} = {\sqrt[{{\mathtt{{\mathtt{12}}}}}]{{\mathtt{b}}}}$$
$${\left({\left({{\mathtt{a}}}^{{\mathtt{4}}}{\mathtt{\,\times\,}}{{\mathtt{b}}}^{{\mathtt{6}}}\right)}^{\left({\frac{{\mathtt{1}}}{{\mathtt{3}}}}\right)}\right)}^{\left({\frac{{\mathtt{1}}}{{\mathtt{4}}}}\right)}$$ = $${{\mathtt{a}}}^{\left({\frac{{\mathtt{4}}}{\left({\mathtt{3}}{\mathtt{\,\times\,}}{\mathtt{4}}\right)}}\right)}{\mathtt{\,\times\,}}{{\mathtt{b}}}^{\left({\frac{{\mathtt{6}}}{\left({\mathtt{3}}{\mathtt{\,\times\,}}{\mathtt{4}}\right)}}\right)}$$ = $${{\mathtt{a}}}^{\left({\frac{{\mathtt{1}}}{{\mathtt{3}}}}\right)}{\mathtt{\,\times\,}}{{\mathtt{b}}}^{\left({\frac{{\mathtt{1}}}{{\mathtt{2}}}}\right)} = {\sqrt[{{\mathtt{{\mathtt{3}}}}}]{{\mathtt{a}}}}{\mathtt{\,\times\,}}{\sqrt{{\mathtt{b}}}}$$