TheXSquaredFactor

The steps are not too long-winded luckily. Unfortunately for Cphill, the 3 that precedes the argument is missing from Cphill's answer. 

1) As Cphill mentioned, if \(f(x)\) is the original function, then \(f(x-6)\) translates the function 6 units rightward. The instructions specificially request for the answer with an equation of \(g(x)\) in terms of \(f(x)\), \(g(x)=f(x-6)\)

2) In the previous answer, we determined that \(g(x)=f(x-6)\), so we can use this information to solve for the current problem:

3) If \(g(x)\) is translated 7 units downward to obtain \(j(x)\), then \(g(x)-7=j(x)\). Of course, the question asks for the equation to be in terms of f(x):

4) Find j(x) in terms of x:
 

The second one was definitely much harder for me to come up with! Here is a picture that may be useful to reference as I solve:

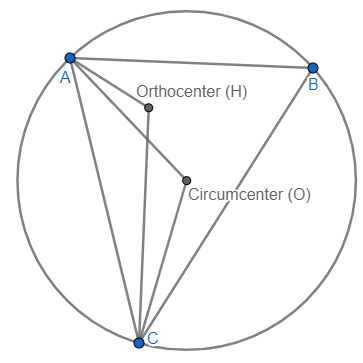
You will probably notice that I added a circle that inscribes the triangle. At its bost basic level, the circumcenter is a point that is equidistant from all the vertices of the triangle. The circumcenter is also the center of a triangle's circumcircle, which I have illustrated with the diagram above. Of course, we know that the sum of \(\angle AHC\) and \(\angle AOC\) is 240 by the given info. Notice that \(m\angle AOC=m\angle AHC\) because they both intercept the same arc. Therefore, we can solve for the angle of the circumcenter.

Notice that \(\angle ABC\) is an inscribed angle, which means that its measure is equal to half the measure of the central angle.

I have been thinking about these two problems for some time, and I think I have finally cracked them! I'll now impart my knowledge to you!
 

1) 

Well, this is taking some time... 

Anyway, \(\triangle AOB\) is another isosceles triangle. \(m\angle OAB=m\angle B=45^\circ\), so the remaining angle, \(\angle BOA=90^\circ\)

By the given information, we know the following:

\(t(x)=\sqrt{3x+1}\\ f(x)=5-t(x)\)

In order to find \(t(f(5))\), we must first evaluate f(x) when x=5:

Now we know that \(t(f(5)=t(1)\) since we just determined that \(f(5)=1\).

Therefore, \(t(f(5))=2\)

Cphill and Guest have providing their individual ways of thinking about it. I think I will, too!

\(\boxed{2009}=\hspace{5mm}1+3+5+...+2003+2005+2007+2009\\ \boxed{2008}=\underline{-(2+4+6+...+2004+2006+2008)}\\ \hspace{19mm}\underbrace{-1-1-1-...-1-1-1}\hspace{21mm}+2009\\ \hspace{33mm}\text{1004 times}\)

Therefore, we have concluded that the complicated expression has been reduced to something relatively simple.

\(-1*1004+2009\\ -1004+2009\\ 1005\)

This is exactly what everyone else got!

"Area" is an ambiguous term when referring to three-dimensional shapes. "Area" could refer to the following:

• Surface Area
• Area of a Face

For a regular tetrahedron, the surface area is as follows:

\(SA=a\sqrt{3}\)

The area of a face for a regular tetrahedron is as follows:

\(A_{\text{face}}=\frac{a^2\sqrt{3}}{4}\)

In both cases, "a" represents the length from one vertex to another.

I do not see how this question is relevant to quotients, but I will evaluate the expression assuming that the "x" represents a multiplication operator. 

6*4*60*68*45+45*23+34*34*5*67*78*90*98=266423797035
 

Understandably, square roots cause a lot of confusion. This is one prime example of this occurring. To be clear, by definition, \(i=\sqrt{-1}\). When you calculate the square root of a number, it is implied that the output is the principal root or the positive result. 

For example, 

\(\sqrt{4}=2\\ \sqrt{9}=3\)

However, if you place a negative sign before the square root, then it is implied that the output should be negative. 

\(-\sqrt{4}=-2\\ -\sqrt{9}=-3\)

If a plus-minus sign precedes a square root, then both answers are desired:

\(\pm\sqrt{4}=\pm2\\ \pm\sqrt{9}=\pm3\)

This confuses many people, and it leads to misconceptions. Since \(\sqrt{-1}\) implies the principal root, the only answer is \(i\).

Examine the false proof that your "guy" provided, which seems to prove that i equals plus or minus 1 to the untrained eye.

\(i^2\\ i^\frac{4}{2}\\ \left(i^4\right)^{0.5}\\ i^{(2+2)^{0.5}}\\ \textcolor{red}{\left(i^2*i^2\right)^{0.5}}\)

The step highlighted in red in an invalid step. It ignores the part about exponent towers. In line 4, you have to evaluate the innermost exponent first to abide by order of operations. In line 5, there are now parentheses around the \(i^2*i^2\), which changes the overall value of the expression.  If this is unclear for you, maybe I will try a simpler example. 

Consider the following two expressions \(2^{3^2}\text{ and }\left(2^3\right)^2\)? The expressions here have a subtle difference, but the output is different. You compute these differently, too. This is another area where misconceptions are prevalent.

\(2^{\textcolor{red}{3^2}}=2^9=512\\ \textcolor{red}{\left(2^3\right)}^2=8^2=64\)

Notice that in the second expression that the parentheses take precedence over any other operation, so you must do that first. Now, let's relate that to the false proof.

\(i^{(2+2)^{0.5}}=\textcolor{red}{i^{4^{0.5}}}=i^2=-1\\ (i^2*i^2)^{0.5}=(i^{2+2})^{0.5}=\textcolor{red}{\left(i^4\right)^{0.5}}\)

Do you notice the discrepancy now? You can now see that the values are different. Since I have cleared up that confusion, I will now end the debate about which complex number the product simplifies to. I'll jump right to the moment of the confusion, which occurs at \(18+3i-3i^2\)

Well, trial and error appeared to be my friend here. If I was not aware that the original expression could be simplified further, I probably would have made the same conclusion as you did, Melody. It is considered improper to have radicals or fractional exponents in the denominator, so I knew that there was some way to simplify this. My method is really only relevant to this particular problem. You will see why. 

Now, let's consider that extra bit on the end, the \(9^\frac{1}{3}=\left(3^2\right)^\frac{1}{3}=3^\frac{2}{3}=3^{\left(\frac{1}{3}\right)^2}\). This means that the denominator can be written like \(1+3^\frac{1}{3}+3^{\left(\frac{1}{3}\right)^2}\), and if I let \(x=3^\frac{1}{3}\), then I can represent the denominator like \(x^2+x+1\). I then made a stunning realization. This required some extraordinary observational skills. 

So, no, the conjugate is not "magical." The only issue with this thought process is that this will not help you on most types of problems with multi-term denominators. This is just one particular case, and I happened to crack it. 

I think your logic is not correct, unfortuantely. If you have heard the story, you have not necessarily "related the story to others." Let's say, for example, that there were 20 storytellers. Since each storyteller tells 2 people, there are 40 people who have been told the story. Now, 60 know about the story, only 20 of which are now storytellers, or "parents."

When you solved and you got 671, you found the number of people who know the story to be 671, but the prompt explains that only 335 people know the story. If I am understanding the problem correctly, 335 should go in for the number of people who know the story, or the "Number of vertices"

\(335=2x+1\\ 334=2x\\ 167=x\)

167 equals the number of parents, or the number of storytellers.