This method is somewhat different than the guest's because it does not need to consider the amount of Cl2 reacted. The general conversion strategy for this particular procedure goes as follows. The table displays the general layout, and all unknowns are marked with question marks:
\(\text{grams}\rightarrow\text{moles}\rightarrow\text{moles}\rightarrow\text{grams}\)
| \(16.2g\text{H}_2\) | \(1\text{molH}_2\) | \(?\text{molHCl}\) | \(?g\text{HCl}\) |
| \(?g\text{H}_2\) | \(?\text{molH}_2\) | \(1\text{molHCl}\) |
Let's travel through this table column by column. We start with the given information, 16.2gH2, and the eventual goal is to perform a series of conversions. The first column of the table is already finished.
The second column asks the following question: How many grams of H2 are in one mole of H2? In order to answer this question, we have to reference the indispensable periodic table of the elements. I generally use https://www.ptable.com/
as an electronic version of the table.
The atomic mass of an element is also the molar mass represented in grams, so H has a molar mass of 1.008g. However, realize that we are finding the molar mass of H2. The subscript indicates that there are two hydrogen molecules, so double the original molar mass, 1.008g, to obtain the molar mass of H2. \(1\text{molH}_2=1.008g*2=2.016g\).\(\)
The third column is quite a simple step, actually. It compares the molar ratio of the two molecules in question, HCl and H2, in this case. Determining this information requires some basic knowledge of a balanced equation. In the given chemical reaction, it is possible to perceive it in the following sense: One molecule of H2 reacts and yields two molecules of HCl. The number of molecules contained in a mole equals Avagadro's constant, or \(1\text{mol}=6.02*10^{23}\text{ molecules}\). If you continue this logic, the original balanced equation indicates \(1\text{molH}_2=2\text{molHCl}\).
The procedure for the fourth column is identical to the procedure for the second column. How many grams of HCl equals one mole of HCl? Because HCl is a compound, the combined mass of the elements equals its molar mass. As aforementioned, H has a mass of 1.008g per mole. Cl, according to the trusty periodic table, has a mass of 35.45g per mole. Therefore, \(1\text{molHCl}=1.008g+35.45g=36.458g\).
After all this work, we have finally determined all the missing values in the original conversion that I suggested earlier. The table now looks complete.
| \(16.2g\text{H}_2\) | \(1\text{molH}_2\) | \(2\text{molHCl}\) | \(36.458g\text{HCl}\) |
| \(2.016g\text{H}_2\) | \(1\text{molH}_2\) | \(1\text{molHCl}\) |
This table is really a fancy representation of three ratios.
| \(16.2g\text{H}_2* \frac{1\text{molH}_2}{2.016g\text{H}_2}* \frac{2\text{molHCl}}{1\text{molH}_2}* \frac{36.458g\text{HCl}}{1\text{molHCl}}\) | First and foremost, let's cancel out all the common units. Doing this shows that the only unit remaining is the desired unit. |
| \(16.2* \frac{1}{2.016}* \frac{2}{1}* \frac{36.458g\text{HCl}}{1}\) | Now it is a matter of simplifying. When I input this entire expression into the calculator, I get an answer close to what the guest got. |
| \(586.0g\text{HCl}\) | |
I default to this method because it removes the need to approximate halfway through the calculation.
I think I can answer #1
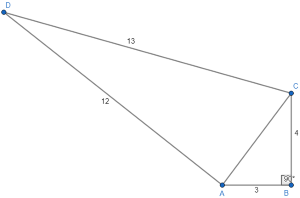
The diagram below meets all the given criteria. It is a quadrilateral with the given side lengths. Since \(\overline{AC}\) is the hypotenuse of \(\triangle ABC\), we can use the Pythagorean Theorem to find the length of the missing side length. Of course, this triangle satisfies the most famous pythagorean triple, a 3-4-5 right triangle, so \(AC=5\).
Yet again, \(\triangle DAC\) is in a similar situation. It is a 5-12-13 triangle, which is another Pythagorean triple. Because of this, \(m\angle DAC=90^\circ\).
I can break up the area of the original quadrilateral into two smaller parts: the 3-4-5 right triangle and the 5-12-13 right triangle.
Using the formula \(A_{\triangle}=\frac{1}{2}bh\), one can identify the areas of both triangles. This process is even simpler since the height of both triangles is also the perpendicular height.
| \(A_1=\frac{1}{2}*3*4\\ A_1=2*3\\ A_1=6\) | \(A_2=\frac{1}{2}*5*12\\ A_2=6*5\\ A_2=30\) |
Now, just add the areas together.
\(A_1+A_2=A_{\text{total}}\\ 6+30=36\text{units}^2\)
Many of the questions seem to suggest that there is a complementary diagram or some missing information (2, 3, 5 and 6)
.#10, why not?
According to the original relation, \(f(x)=\sqrt[3]{x-4}\). There are a few steps that need to be done in order to find the inverse.
#1) Convert to y=-notation. I find that it is easier when working with this notation. This is quite a simple step, wouldn't you agree?
\(f(x)=\sqrt[3]{x-4}\Rightarrow y=\sqrt[3]{x-4}\)
#2) Now, replace all instances of a "y" with an "x," and replace all instances of an "x" with a "y." This is not a difficult step, either, as you might imagine.
\(y=\sqrt[3]{x-4}\Rightarrow x=\sqrt[3]{y-4}\)
#3) Solve for y. This step can range in difficulty. In this case, it is quite a simple step.
| \(x=\sqrt[3]{y-4}\) | Cube both sides. |
| \(x^3=y-4\) | Add 4 to both sides to isolate y. |
| \(y=x^3+4\) | |
#4) Convert back to function notation since the original problem was given in function notation. This is quite simple, too.
\(y=x^3+4\Rightarrow f^{-1}(x)=x^3+4\)
#5) Correspond your answer with the answer choices given!
To solve for a variable, in this case, simpl means to isolate it. That is the goal of solving for a variable.
1)
| \(C=K\left(\frac{Rr}{R-r}\right)\) | Let's first multiply both sides by (R-r). This will eliminate the denominator, which will ease the process of solving for "K." |
| \(C(R-r)=KRr\) | Divide by Rr to isolate K. |
| \(K=\frac{C(R-r)}{Rr}\\\) | You could distribute, if you so desired, but it is not necessary. This just creates more work for yourself, anyway. This is the final answer. |
2) This one will be harder since two "R's" exist in the original equation. This generally signals for the use of grouping.
| \(C=K\left(\frac{Rr}{R-r}\right)\) | Let's do the exact same thing as before; multiply by R-r. |
| \(C(R-r)=KRr\) | Let's distribute the C into the binomial. This will allow us to have two terms with "R's" |
| \(CR-Cr=KRr\) | Let's subtract KRr from both sides. Let's add Cr to both means meanwhile. |
| \(CR-KRr=Cr\) | Using grouping, we can change this into one "R." |
| \(R(C-Kr)=Cr\) | Now, divide by C-Kr to isolate "R." |
| \(R=\frac{Cr}{C-Kr}\) | This is finished because we have isolated the R. |
3) We will have to utilize the same technique in number 2 in order to isolate "f."
| \(F=\frac{fg}{f+g-d}\) | Let's multiply the denominator on both sides. This will get rid of any and all pesky denominators in this equation, |
| \(F(f+g-d)=fg\) | There is a "g" in the trinomial, so we will have to expand that part. |
| \(Ff+Fg-Fd=fg\) | Move all terms with a factor of f on the left hand side. Any other terms are moved to the right hand side. |
| \(Ff-fg=-Fg+Fd\) | Factor out an "f" from both terms from the left hand side. |
| \(f(F-g)=-Fg+Fd\) | Finally, divide by F-g to isolate the wanted variable completey. |
| \(f=\frac{-Fg+Fd}{F-g}\) | No more simplification is possible here. Leave the fraction as is. |
For the second question, it is possible to utilize something known as the Pythagorean Inequality Theorem. The theorem actually has two parts, but the relevant portion for this particular problem is that if the square of a triangle's longest side length is greater than the the sum of the squares of the shorter side lengths, then the triangle is obtuse. This wording is quite verbose, I know, so I decided to create a visual aide as a reference for you!

Let's first try and identify what the longest side length is of this particular triangle is. We know that 16 and 21 are already defined lengths, but we also have the unknown side length, which is labeled as s. I will follow the visual aide above, and I will consider the longest side length to be of length "c." In the visual aide above, the shorter side lengths are labeled "a" and "b."
It is easy to exclude the side with length 16 as the longest side length since we know that there exists a side with length 21, which is longer. However, beyond this, there are two possibilities. The possibility is that:
Of course, we do not know which one is the longest side, so we will just have to assume both cases. Let's begin with assuming that "s" is the longest side, or our "c."
| \(c^2>a^2+b^2\) | "s" will be the longest side, so plug it into "c." Plug the other two side lengths in any order. | ||
| \(s^2>21^2+16^2\) | Now, solve for "s" to see what the possibilities are. | ||
| \(s^2>441+256\) | |||
| \(s^2>697\) | Take the square root of both sides. This results in an absolute value inequality. | ||
| \(|s|>\sqrt{697}\) | Of course, the absolute value splits the equation into two parts. | ||
| Of course, let's remember that "s" is an integer side length of a triangle, so "s" must be positive. We can reject the second inequality because those values include ones less tha zero. | ||
| \(s>\sqrt{697}\) |
The above algebra only solved the first case where we assumed that "s" is the longest side. Now, let's assume that the side with length 21 is the indeed the longest.
| \(21^2>16^2+s^2\) | Let's solve for "s" here by simplifying first and foremost. | ||
| \(441>256+s^2\) | Subtract 256 from both sides. | ||
| \(185>s^2\\ s^2<185\) | For me, I can interpret the inequality better when the variable is placed on the left hand side of the equation. Take the square root of both sides. | ||
| \(|s|<\sqrt{185}\) | Now, solve the absolute value inequality. | ||
| Unlike the previous inequality, we can combine this into one compound inequality. | ||
| -√185 < s < √185 | Of course, yet again, "s" is a side length, so it should be greater than zero. | ||
| 0 < s < √185 |
Of course, let's take clean this up. We know, by the given information, that we only care about integer solutions, so let's calculate the radicals.We now have set restrictions for "s." \(\)
√697 ≈ 26.40
√185 ≈ 13.60
We can then make the restrictions the following
We are not done yet, though! We have to take into account the side length restriction that Cpill figured out in part a! He found that 5 < s < 37
Therefore, integer sides with lengths 6 to 13 or sides with lengths 27 to 36 are possible. We can find the total number of integer solutions by figuring out how many integers are in this range.
From [6,13], there are 8 integers
From [27,36], there are 10 integers
Altogether, there are 18 integer solutions.
*Unfortunately, LaTeX appears to be funky when compound inequalities are introduced, so I have resorted to a different method to portray them.