amygdaleon305

Suppose Hugo had \(x\) money at first.

Hugo gave 1/4 of his money and an additional 1 to Cavin

Remaining money with Hugo \(=x-{1\over 4}x-1\)

                                               \(={3\over 4 }x-1\)

He gave 1/5 of the remaining money and an additional 4 to Kenneth

Remaining money with Hugo \(= ({3\over 4}x-1)-{1\over 5}({3\over 4}x-1)-4\) 

                                               \(={3\over 4}x-1-{3\over 20}x+{1\over 5}-4\)

                                               \(={12\over 20}x-{24\over 5}\)

Now according to question, 

⇒\({12 \over 20}x-{24\over 5}={1\over 5}({3\over4}x-1)+4+31\)

⇒\({12\over 20}x-{24\over 5}={3\over 20}x-{1\over 5}+35\)

⇒\({12\over 20}x-{24\over 5}={3\over 20}x+{174\over 5}\)

⇒\({9\over 20}x={198\over 5}\)

⇒\(x=88\)

∴ Hugo had 88 at first.

Now, amt. of money Hugo gave to Calvin \(={1\over 5}({3\over 4}x-1)+4\)

                                                                  \(={1\over 5}(65)+4\)

                                                                  \(=17\)

Thus, Hugo gave 17 units money to Calvin. 

~Amy                                         

Are you sure its an arithmetic sequence shouldn't it be a geometric sequence? 

In which case, 

sequence should be : \(3^2, x, 3^6\)

∴ Value of \(x= 3^4\)

You flatter me Phill!! Thank you!! 

Terri and Candace can mow the lawn in 18 min. 

⇒In 1 min Terri and Candace can mow = \({1 \over 18}\) part of the lawn

Candace alone can mow the lawn in 30 min

⇒ In 1 min Candace can mow = \({1\over 30}\) part of the lawn

So, in 1 min Terri alone can mow  \(=({1\over 18} - {1\over 30})\) part of the lawn

                                                      \(={12 \over 540}\)

                                                      \(={1 \over 45}\) 

∴ Terri alone can mow the lawn in 45 min. 

~Amy 

\(\sqrt{{6y+2}\over 2y+2}= {5\over 2}\)

Now, squaring both sides

\({{6y+2}\over {2y+2}}= {25 \over 4}\)

Cross-multiplying both sides, 

\(24y+8=50y+50\)

\(26y=42\)

⇒\(y= {21 \over 13}\)

Value of y is \({21 \over 13}\). 

~ Amy 

We have the following system of  equations - 

  \(a+2b+3c+4d=10\)

  \(4a+b+2c+3d=4\)

  \(3a+4b+c+2d=-10\)

  \(2a+3b+4c+d=-4\)

Adding all of them, 

⇒\(10a+10b+10c+10d=10-10+4-4\)

⇒\(10(a+b+c+d)=0\)

⇒\(a+b+c+d=0\)

∴ The value of a+b+c+d is 0. 

P.S. This maybe due to the reason that either pair of a,b,c,d amount to 0 due to summing of negative and positive integers. 

Total no. of balls \(=3+4+5\) 

                           \(=12\)

3 balls are drawn without replacement. 

⇒ No. of ways of choosing 3 balls \(=\binom{12}{3}\)

                                                       \(=220\)

Case 1: All are same color. 

Favourable outcomes \(=\binom{3}{3}+\binom{4}{3}+\binom{5}{3}\)

                                   \(=1+4+10\)

                                   \(=15\)

∴ P(same color balls) \(= {15\over 220}\)

                                   \(={3 \over 44}\)

Thus, the probability that they're same color is \(3 \over 44\).

Case 2: All are different colors.

Favourable outcomes \(=\binom{3}{1}*\binom{4}{1}*\binom{5}{1}\)

                                   \(=3*4*5\)

                                    \(=60\)

∴ P(different color balls) \(={60 \over 220}\)

                                       \(={3 \over 11}\)

Thus, the probability that they're of different colors is \(3 \over 11\).

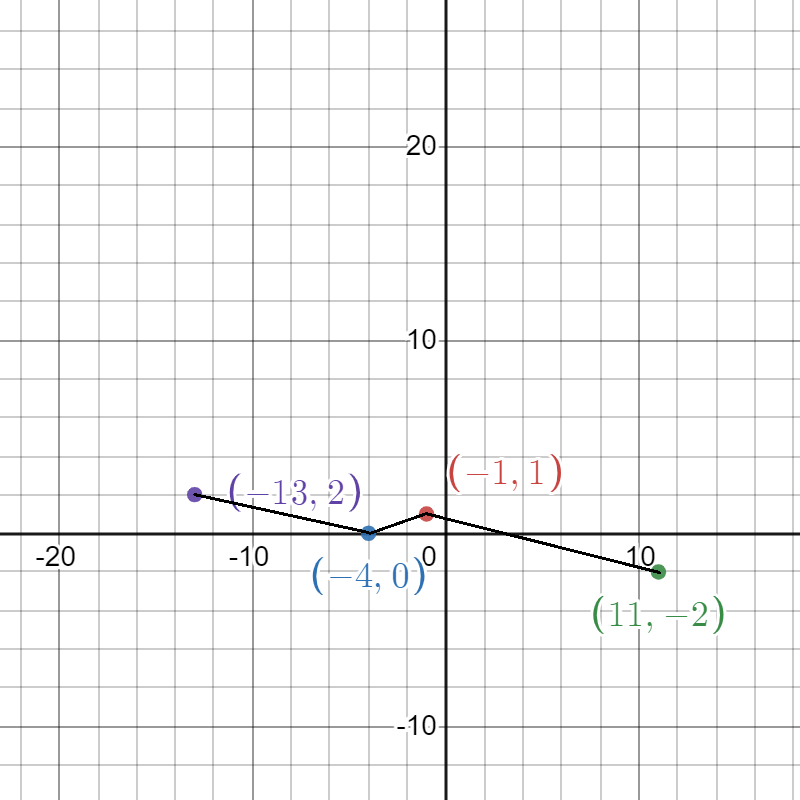
a) In order to plot g(x) we translate the endpoints of f(x)  as follows :- 

       \((-4,4)\) in f(x) ⇔ \((-13,2)\) in g(x) 

       \( (0,2)\) in f(x) ⇔ \((-1,1)\) in g(x) 

       \((-1,0)\) in f(x) ⇔ \((-4,0)\) in g(x)

       \((4,-4)\) in f(x) ⇔ \((11,-2)\) in g(x)

   ∴ The graph of g(x) is plotted below -

________________________________________________________________________________________________________

b) Each point \((a,b)\) in  f(x) becomes \((3a-1,{b \over 2})\) in g(x).

    Now, that implies a horizontal stretch by a factor of 3 and a horizontal shift by 1 unit left for a. 

    So, that gives us \(f({1 \over 3}.(x+1))\)

    As for b, the graph shrinks vertically by a factor of \(1\over 2\). 

    So that gives \({1\ \over 2}f({1 \over 3}.(x+1))\)

    So that completes, 

     \(g(x) = {1 \over 2}f({x+1 \over 3})\)

_______________________________________________________________________________________________________

c) In order to get the graph \(y=g(x)\), the original graph can be stretched horizontally  by a factor of 3, then shrunk vertically by a factor of 1/2 and shifted left by 1 unit. 

_________________________________________________________________________________________________________

~ It's a pleasure! :) 

Let's assume Dave had \(x\) apples at first. 

⇒ Alex had = \(2x\) apples

When Dave gave 10 apples to Alex, he had 8 times as many apples as Dave in the end.

∴ According to question, 

\(2x+10=8(x-10)\)

\(2x+10=8x-80\)

\(6x=90\)

⇒\(x=15\)

Thus, Alex had 30 apples at first.

First of all, I think there's a small error in the expression given, 

However minute it may seem it can confuse easily... So the correction is 

                      \(3(-10)+2[3/2(-10)]+4[1/4(20)]+5(20) \)

Now, after referring the steps we see that Sal made his first error in step 2. 

∴ The correction is here as follows - 

\(3(-10)+2[{3\over 2}.-10]+4[{1\over 4}.20]+5(20) = 3(-10)+2(-15)+4(5)+5(20) \)

                                                                       \(=-30-30+20+100\)

                                                                       \(=60\)

∴ The final answer is 60.