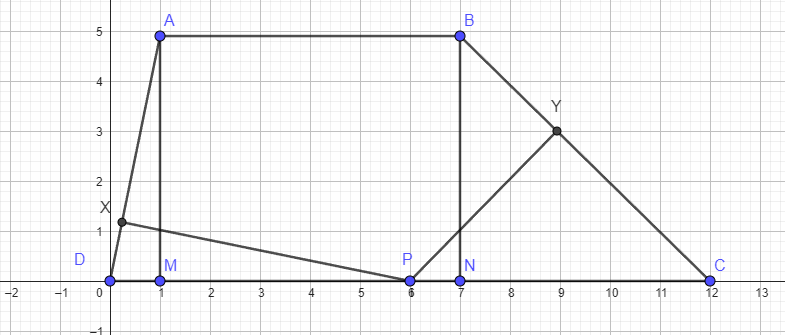
Draw AM , BN perp to CD
Let DN = x
CN = 12 - ( AB + DN) = 12 - (6 + x) = 6-x
AM = BN
So....By the Pythagorean Theorem
AD^2 - DM^2 = BC^2 - CN^2
5^2 - x^2 = 7^2 - ( 6-x)^2
25 - x^2 = 49 - x^2 + 12x - 36
25 = 12x + 13
12 = 12x
x =1 = DM
Note that we have two right triangles ADM and PDX
Angles AMD and PXD are equal = 90°
And angle ADM = angle PDX
So triangle ADM is similar to triangle PDX
PD / AD = 6/5
So
DX / DM = 6/5
DX = (6/5)DM = (6/5) (1) = 6/5
So
sqrt [DP^2 - DX^2] = PX
sqrt [ 6^2 - (6/5)^2 ] = sqrt [ 36*25 - 36 ] / 5 = sqrt [ 900 - 36] / 5 = sqrt [ 864] / 5 =
sqrt [ 144 * 6 ] / 5 = 12sqrt (6) / 5 = PX
Similarly
Right Triangles BCN and PCY are similar
PC/BC = 6/7
So
CY / CN = 6/7
CY / 5 = 6/7
CY = 30/7
So
sqrt [ PC^2 - CY^2 ] = PY
sqrt [ 6^2 - (30/7)^2] = sqrt [ 36 * 49 - 900 ] / 7 = sqrt [ 1764 - 900] / 7 = sqrt [ 864]/7 =
sqrt [ 144 *6 ] / 7 = 12sqrt(6) / 7 = PY


