heureka

In the prime factorization of 109!, what is the exponent of 3?
(Reminder: The number n! is the product of the integers from 1 to n. For example, 5! = 5 * 4 * 3 * 2* 1 = 120.)

\(\begin{array}{|rcll|} \hline \dfrac{109}{3^1} &=& [36].3333333333 \\\\ \dfrac{109}{3^2} &=& [12].1111111111 \\\\ \dfrac{109}{3^3} &=& [4].03703703704 \\\\ \dfrac{109}{3^4} &=& [1].34567901235 \\\\ \dfrac{109}{3^5} &=& [0].44855967078 \\\\ \ldots &=& [0] \\\\ \hline & \text{sum} =& 36+12+4+1 =\mathbf{ 53} \\ \hline \end{array}\)

The exponent of \(\mathbf{3}\) is \(\mathbf{53}\)

Vectors:

a)
Find CB:

\(\begin{array}{|rcll|} \hline -DC+DA+AB&=& CB \\ -p+2q-p+5p &=& CB \\ 2q + 3p &=& CB \\ \mathbf{\vec{CB}} & \mathbf{=} & \mathbf{2q + 3p} \\ \hline \end{array}\)

b)

\(\begin{array}{|rcll|} \hline AQ &=& \dfrac25 AB \quad & | \quad AB =5p \\ &=& \dfrac25 \cdot 5p \\ \mathbf{AQ} & \mathbf{=} & \mathbf{2p} \\\\ QB &=& \dfrac35 AB \quad & | \quad AB =5p \\ &=& \dfrac35 \cdot 5p \\ \mathbf{QB} & \mathbf{=} & \mathbf{3p} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \dfrac{DA}{2}+PQ+QB-CB-DC &=& 0 \quad | \quad DA =2q-p \quad QB = 3p \quad DC = p \\ \dfrac{2q-p}{2}+PQ+3p-CB-p &=& 0 \\ \dfrac{2q-p}{2}+PQ+2p-CB &=& 0 \\ \dfrac{2q-p}{2}+PQ+2p &=& CB \\ && \mathbf{\vec{CB}=2q + 3p} \\ && 2q = CB - 3p \\ && q = \dfrac{CB - 3p}{2} \\ \dfrac{2\left(\dfrac{CB - 3p}{2}\right)-p}{2}+PQ+2p &=& CB \\ \dfrac{CB - 3p-p}{2}+PQ+2p &=& CB \\ \dfrac{CB - 4p}{2}+PQ+2p &=& CB \\ \dfrac{CB}{2} - 2p+PQ+2p &=& CB \\ \dfrac{CB}{2}+PQ&=& CB \\ PQ&=& CB -\dfrac{CB}{2} \\ \mathbf{PQ} & \mathbf{=} & \mathbf{\dfrac12\cdot CB} \\ \hline \end{array}\)

Vectors:

\(\begin{array}{|lrcll|} \hline (1) & a+b &=& RS \\\\ (2) & 2a+2b+BA &=& 2c \\ & BA &=& 2\left(c-(a+b)\right) \\\\ (3) & c+PQ - \dfrac{BA}{2} &=& 2(a+b) \\ &c+PQ- \dfrac{2\left(c-(a+b)\right)}{2} &=& 2(a+b) \\ &c+PQ- \left(c-(a+b) \right) &=& 2(a+b) \\ &c+PQ-c+(a+b) &=& 2(a+b) \\ &PQ +(a+b) &=& 2(a+b) \\ &PQ &=& 2(a+b)-(a+b) \\ &PQ &=& a+b \quad & | \quad a+b = RS \\ &\mathbf{PQ} & \mathbf{=} & \mathbf{RS} \\ \hline \end{array}\)

A closed form for the sum $$ S = \frac {2}{3+1} + \frac {2^2}{3^2+1} + \cdots + \frac {2^{n+1}}{3^{2^n}+1} $$
is $1 - \frac{a^{n+b}}{3^{2^{n+c}}-1},$ where $a$, $b$, and $c$ are integers. Find $a+b+c$.

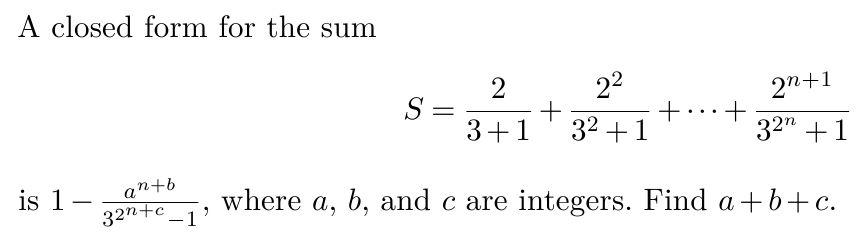
Formula:

\(\begin{array}{|rclcl|} \hline s_n &=& \dfrac{2}{3+1} + \dfrac{2^2}{3^2+1} + \dfrac{2^3}{3^{(2^2)}+1} + \dfrac{2^4}{3^{(2^3)}+1} + \dfrac{2^5}{3^{(2^4)}+1} + \ldots + \dfrac{2^{n+1}}{3^{(2^n)}+1} \\\\ s_0 &=& \dfrac12 \\ s_1 &=& \dfrac12 + \dfrac{4}{10} = \dfrac{9}{10} \\ s_2 &=& \dfrac{9}{10}+ \dfrac{8}{82}= \dfrac{409}{410} \\ s_3 &=& \dfrac{409}{410}+ \dfrac{16}{6562}= \dfrac{1345209}{1345210} \\ \ldots \\ \hline \end{array} \)

\(\begin{array}{|rcll|} \hline s_n &=& 1 - \dfrac{a^{n+b}}{3^{ (2^{n+c} )}-1} \\\\ s_n &=& 1 - \dfrac{a^n a^b} { 3^{ (2^n 2^c )}-1 } \\\\ s_n &=& 1 - \dfrac{a^n a^b} { \left(3^{(2^c)} \right)^{2^n}-1 } \\ && \text{Set }~ \alpha=a^b \\ && \text{Set }~ \gamma=3^{(2^c)} \\ \mathbf{s_n} & \mathbf{=} & \mathbf{1 - \dfrac{a^n \alpha} { \gamma^{(2^n)}-1 } } \\ \hline \end{array}\)

\(\begin{array}{rcll} \boxed{n=0}:\\ s_0 = \dfrac12 &=& 1 - \dfrac{a^0 \alpha} { \gamma^{(2^0)}-1 } \\ \dfrac12 &=& 1 - \dfrac{\alpha} { \gamma-1 } \\ \dfrac{\alpha} { \gamma-1 } &=& 1 - \dfrac12 \\ \dfrac{\alpha} { \gamma-1 } &=& \dfrac12 \\ \mathbf{ \alpha } & \mathbf{=}& \mathbf{ \dfrac12\cdot (\gamma-1)} \qquad (1) \\ \end{array} \)

\(\begin{array}{rcll} \boxed{n=1}:\\ s_1 = \dfrac{9}{10} &=& 1 - \dfrac{a^1 \alpha} { \gamma^{(2^1)}-1 } \\ \dfrac{9}{10} &=& 1 - \dfrac{a \alpha} { \gamma^2-1 } \\ \dfrac{a \alpha} { \gamma^2-1 } &=& 1 - \dfrac{9}{10} \\ a\alpha & = & \dfrac{1}{10}\cdot (\gamma^2-1) \quad & | \quad \gamma^2-1 = (\gamma-1)(\gamma+1) \\ \mathbf{ a\alpha } & \mathbf{=}& \mathbf{ \dfrac{1}{10}\cdot (\gamma-1)(\gamma+1)} \qquad (2) \\ \end{array}\)

\(\begin{array}{rcll} \boxed{n=2}:\\ s_2 = \dfrac{409}{410} &=& 1 - \dfrac{a^2 \alpha} { \gamma^{(2^2)}-1 } \\ \dfrac{409}{410} &=& 1 - \dfrac{a^2 \alpha} { \gamma^4-1 } \\ \dfrac{a^2 \alpha} { \gamma^4-1 } &=& 1 - \dfrac{409}{410} \\ a^2 \alpha &=& \dfrac{1}{410}(\gamma^4-1) \quad | \quad \gamma^4-1 = (\gamma^2-1)(\gamma^2+1)= (\gamma-1)(\gamma+1)(\gamma^2+1) \\ \mathbf{ a^2\alpha } & \mathbf{=}& \mathbf{ \dfrac{1}{410}\cdot (\gamma-1)(\gamma+1)(\gamma^2+1)} \qquad (3) \\ \end{array}\)

\(\mathbf{a=~ ?}\)

\(\begin{array}{|rcll|} \hline \mathbf{ a\alpha } & \mathbf{=}& \mathbf{ \dfrac{1}{10}\cdot (\gamma-1)(\gamma+1)} \qquad (2) \quad & | \quad \mathbf{ \alpha = \dfrac12\cdot (\gamma-1)} \qquad (1) \\ a\cdot \dfrac12\cdot (\gamma-1) & = & \dfrac{1}{10}\cdot (\gamma-1)(\gamma+1) \\ a\cdot \dfrac12 & = & \dfrac{1}{10}\cdot (\gamma+1) \\ \mathbf{a} & \mathbf{=} & \mathbf{\dfrac{1}{5}\cdot (\gamma+1)} \qquad (4) \\ \hline \end{array} \)

\(\mathbf{\gamma=~ ?}\)

\(\begin{array}{|rcll|} \hline \mathbf{ a^2\alpha } & \mathbf{=}& \mathbf{ \dfrac{1}{410}\cdot (\gamma-1)(\gamma+1)(\gamma^2+1)} \qquad (3) \\\\ && \mathbf{a = \dfrac{1}{5}\cdot (\gamma+1)} \quad (4) \qquad \mathbf{ \alpha = \dfrac12\cdot (\gamma-1)} \quad (1)\\\\ \dfrac{1}{25}\cdot (\gamma+1)^2\cdot \dfrac12\cdot (\gamma-1) & = & \dfrac{1}{410}\cdot (\gamma-1)(\gamma+1)(\gamma^2+1) \\ \dfrac{1}{25}\cdot (\gamma+1)\cdot \dfrac12 & = & \dfrac{1}{410}\cdot (\gamma^2+1) \\ \gamma+1 & = & \dfrac{5}{41}\cdot (\gamma^2+1) \\ \gamma+1 & = & \dfrac{5}{41}\gamma^2+\dfrac{5}{41} \\ \dfrac{5}{41}\gamma^2-\gamma-1+\dfrac{5}{41} &=& 0 \\ \dfrac{5}{41}\gamma^2-\gamma- \dfrac{36}{41} &=& 0 \\\\ \gamma &=& \dfrac{ 1\pm \sqrt{1-4\cdot\dfrac{5}{41}\cdot \left(-\dfrac{36}{41} \right) } } {2\cdot \dfrac{5}{41} } \\\\ \gamma &=& \dfrac{ 1\pm \sqrt{1+ \dfrac{720}{41^2} } } {\dfrac{10}{41} } \\\\ \gamma &=& \dfrac{41}{10} \left( 1\pm \sqrt{1+ \dfrac{720}{41^2} } \right) \\\\ \gamma &=& \dfrac{41}{10} \left( 1\pm \dfrac{ \sqrt{2401} } {41} \right) \\\\ \gamma &=& \dfrac{41}{10} \left( 1\pm \dfrac{ 49 } {41} \right) \\\\ \gamma &=& \dfrac{41}{10} \pm \dfrac{41}{10} \cdot \dfrac{49} {41} \\\\ \gamma &=& \dfrac{41}{10} \pm \dfrac{49}{10} \\\\ \gamma &=& \dfrac{41+49}{10} \\\\ \gamma &=& \dfrac{90}{10} \\ \mathbf{ \gamma }& \mathbf{=}& \mathbf{9} \\\\ \gamma &=& \dfrac{41-49}{10} \\\\ \gamma &=& -\dfrac{8}{10} \qquad \text{no solution, } \gamma\gt 0\\ \hline \end{array} \)

\(\mathbf{a=~ ?}\)

\(\begin{array}{|rcll|} \hline a & = & \dfrac15\cdot (\gamma+1) \quad & | \quad \gamma = 9 \\ a & = & \dfrac15\cdot (9+1) \\ a & = & \dfrac{10}{5} \\ \mathbf{a} & \mathbf{=} & \mathbf{2} \\ \hline \end{array}\)

\(\mathbf{\alpha=~ ?}\)

\(\begin{array}{|rcll|} \hline \alpha & = & \dfrac12\cdot (\gamma-1) \quad & | \quad \gamma = 9 \\ \alpha & = & \dfrac12\cdot (9-1) \\ \alpha & = & \dfrac{8}{2} \\ \mathbf{\alpha} & \mathbf{=} & \mathbf{4} \\ \hline \end{array}\)

\(\mathbf{b=~ ?}\)

\(\begin{array}{|rcll|} \hline \alpha &=& a^b \quad & | \quad a=2 \qquad \alpha = 4 \\ 4 &=& 2^b \\ 2^2 &=& 2^b \\ 2 &=& b \\ \mathbf{b} & \mathbf{=} & \mathbf{2} \\ \hline \end{array}\)

\(\mathbf{c=~ ?} \)

\(\begin{array}{|rcll|} \hline \gamma &=& 3^{(2^c)} \quad & | \quad \gamma = 9 \\ 9 &=& 3^{(2^c)} \\ 3^2 &=& 3^{(2^c)} \\ 2 &=& 2^c \\ 2^1 &=& 2^c \\ 1 &=& c \\ \mathbf{c} & \mathbf{=} & \mathbf{1} \\ \hline \end{array}\)

\(\begin{array}{rcll} && \mathbf{a+b+c} \\ &=& 2+2+1 \\ &=& \mathbf{5} \\ \end{array}\)

Find the sum of all positive integral values of n for which

\(\mathbf{\large\dfrac{n+6}{n}}\)

is an integer.

\(\begin{array}{|rcll|} \hline && \mathbf{ \dfrac{n+6}{n}} \\\\ &=& \dfrac{n}{n} + \dfrac{6}{n}\\\\ &=& 1 + \dfrac{6}{n}\\ \hline \end{array}\)

So \(n\) are the divisors of \(6\).

The 4 divisors of 6 are: \(1,2,3,6\)
The sum is \(1+2+3+6 =\mathbf{ 12}\)

(C)
Each of the last two digits must be 5, 7, or 8 ?

\(\begin{array}{|lclc|c|} \hline & x&x &xx \\ \hline &\begin{Bmatrix} 00\\ \vdots \\ 99 \end{Bmatrix} \cdots &\begin{Bmatrix} 5\\7\\8 \end{Bmatrix}\cdots & 5& 100\times 3 \\\\ &\begin{Bmatrix} 00\\ \vdots \\ 99 \end{Bmatrix} \cdots &\begin{Bmatrix} 5\\7\\8 \end{Bmatrix}\cdots & 7& +100\times 3 \\\\ &\begin{Bmatrix} 00\\ \vdots \\ 99 \end{Bmatrix} \cdots &\begin{Bmatrix} 5\\7\\8 \end{Bmatrix}\cdots & 8& +100\times 3 \\\\ \hline & & & & = 3\times 100\times 3 = {\color{red}900} \\ \hline \end{array}\)

There are 900 4-digit positive integers that satisfy the condition.

(B)
The last two digits cannot be the same digit ?

\(\begin{array}{|lcc|c|} \hline & xx &xx \\ \hline &\begin{Bmatrix} 10\\ \vdots \\ 99 \end{Bmatrix}\cdots & 00 & 90 \\\\ &\begin{Bmatrix} 10\\ \vdots \\ 99 \end{Bmatrix}\cdots & 11 & 90 \\\\ &\begin{Bmatrix} 10\\ \vdots \\ 99 \end{Bmatrix}\cdots & 22 & 90 \\\\ & \cdots \\ \\ &\begin{Bmatrix} 10\\ \vdots \\ 99 \end{Bmatrix}\cdots & 99 & 90 \\\\ \hline & & & = 90\times 10 = 900 \\ \hline \end{array}\)

1000 until 9999: There are 9000  four-digit integers.

9000 - 900 = 8100

There are 8100 4-digit positive integers that satisfy the condition.

How many 4-digit positive integers exist that satisfy the following conditions:

(A) Each of the first two digits must be 1, 4, or 5, and

(B) the last two digits cannot be the same digit, and

(C) each of the last two digits must be 5, 7, or 8?

(A)
Each of the first two digits must be 1, 4, or 5 ?

\(\begin{array}{|lllc|c|} \hline & x&x &xx \\ \hline &1 \cdots &\begin{Bmatrix} 1\\4\\5 \end{Bmatrix}\cdots &\begin{Bmatrix} 00\\ \vdots \\ 99 \end{Bmatrix} & 3\times 100 \\\\ &4 \cdots &\begin{Bmatrix} 1\\4\\5 \end{Bmatrix}\cdots &\begin{Bmatrix} 00\\ \vdots \\ 99 \end{Bmatrix} & +3\times 100 \\\\ &5 \cdots &\begin{Bmatrix} 1\\4\\5 \end{Bmatrix}\cdots &\begin{Bmatrix} 00\\ \vdots \\ 99 \end{Bmatrix} & +3\times 100 \\\\ \hline & & & & = 3\times 3\times 100 = {\color{red}900} \\ \hline \end{array} \)

There are 900 4-digit positive integers that satisfy the condition.

b)

(-2x) * (4-3x^2)^-2 dx Grenzen 1 und -1 durch Substitution.

Integral

\(\displaystyle \int \limits_{-1}^{1} \dfrac{-2x}{ (4-3x^2)^2 } \ dx = \ ?\)

\(\begin{array}{|lrcl|} \hline \displaystyle \int \limits_{-1}^{1} \dfrac{-2x}{ (4-3x^2)^2 } \ dx = \ ? \\ & \text{Substitution:}\\ & \mathbf{z} &\mathbf{=}& \mathbf{ 4-3x^2 } \\ & dz &=& -6x \ dx \\ & \mathbf{dx} &\mathbf{=}& \mathbf{-\dfrac{1} { 6x } \ dz} \\ \hline \end{array}\)

Stammfunktion:

\(\begin{array}{|lcl|} \hline \displaystyle \int \dfrac{-2x}{ (4-3x^2)^2 } \ dx \\\\ &=& \displaystyle \int \left( \dfrac{-2x}{ z^2 }\right) \cdot \left(-\dfrac{1} { 6x } \right) \ dz \\\\ &=& \displaystyle \dfrac13\cdot \int \dfrac{1}{ z^2 } \ dz \\\\ &=& \displaystyle \dfrac13\cdot \int z^{-2} \ dz \\\\ &=& \displaystyle \dfrac13\cdot\left( \dfrac{z^{-2+1} }{-2+1} \right) +c \\\\ &=& \displaystyle -\dfrac13\cdot z^{-1} +c \\\\ &=& \displaystyle -\dfrac{1}{3z} +c \\\\ & \text{Rücksubstitution:} \\ &=& \displaystyle -\dfrac{1}{3(4-3x^2)} +c \\\\ \hline \mathbf{\displaystyle \int \limits_{-1}^{1} \dfrac{-2x}{ (4-3x^2)^2 } \ dx} \\ &=& \displaystyle -\dfrac13 \cdot \left[ \dfrac{1}{4-3x^2} \right]_{-1}^{1} \\\\ &=& \displaystyle -\dfrac13 \cdot \left[ \dfrac{1}{4-3\cdot 1^2} - \dfrac{1}{4-3\cdot (-1)^2} \right] \\\\ &=& \displaystyle -\dfrac13 \cdot \left[ \dfrac{1}{1} - \dfrac{1}{1} \right] \\\\ &=& \displaystyle -\dfrac13 \cdot \left[ 1 - 1 \right] \\\\ &=& \displaystyle -\dfrac13 \cdot 0 \\\\ &=& \displaystyle 0 \\\\ \mathbf{\displaystyle \int \limits_{-1}^{1} \dfrac{-2x}{ (4-3x^2)^2 } \ dx} &\mathbf{=}& \mathbf{0} \\ \hline \end{array}\)

c)
x*sin(x^2)dx    Grenzen: 1 und 0 durch Substitution.

Integral

\(\displaystyle \int \limits_{0}^{1} x*\sin(x^2) \ dx = \ ?\)

\(\begin{array}{|lrcl|} \hline \displaystyle \int \limits_{0}^{1} x*\sin(x^2) \ dx = \ ? \\ & \text{Substitution:}\\ & \mathbf{z} &\mathbf{=}& \mathbf{x^2 } \\ & dz &=& 2x \ dx \\ & \mathbf{dx} &\mathbf{=}& \mathbf{\dfrac{1} { 2x } \ dz} \\ \hline \end{array}\)

Stammfunktion:

\(\begin{array}{|lcl|} \hline \displaystyle \int x*\sin(x^2) \ dx \\\\ &=& \displaystyle \int x*\sin(z) \dfrac{1} { 2x } \ dz \\\\ &=& \displaystyle \dfrac12 \cdot \int \sin(z) \ dz \\\\ &=& \displaystyle \dfrac12 \cdot \left(- \cos(z) \right) +c \\\\ & \text{Rücksubstitution:} \\ &=& \displaystyle \dfrac12 \cdot \left(- \cos(x^2) \right) +c \\\\ &=& \displaystyle -\dfrac12 \cdot \left( \cos(x^2) \right) +c \\\\ \hline \mathbf{\displaystyle \int \limits_{-1}^{1} x*\sin(x^2) \ dx} \\ &=& \displaystyle -\dfrac12 \cdot \left[ \cos(x^2) \right]_{0}^{1} \quad |\quad x \text{ in radiant} \\\\ &=& \displaystyle -\dfrac12 \cdot \left[ \cos(1^2)-\cos(0^2) \right] \\\\ &=& \displaystyle -\dfrac12 \cdot \left( \cos(1)-\cos(0) \right) \\\\ &=& \displaystyle -\dfrac12 \cdot \left( 0.54030230587-1 \right) \\\\ &=& \displaystyle -\dfrac12 \cdot \left( -0.45969769413 \right) \\\\ &=& \displaystyle \dfrac12 \cdot \left( 0.45969769413 \right) \\\\ \mathbf{\displaystyle \int \limits_{-1}^{1} x*\sin(x^2) \ dx} &\mathbf{=}& \mathbf{\displaystyle 0.22984884707} \\ \hline \end{array}\)