I do not believe the question can be answered. 3.5 is too small there is no solution.
I think that 3.5 was an approximation, not an exact value. The exact value that they wanted was sqrt(12.8) which is approx 3.5776.
This is an approximation of the smallest possible perimeter of the octagon.
Ok now with the proper explanaton, But I am replacing 3.5 with P which will eventually be replaced with sqrt(12.8)
I discovered lots about rotational symmetry while I was answering this question. It is really cool!
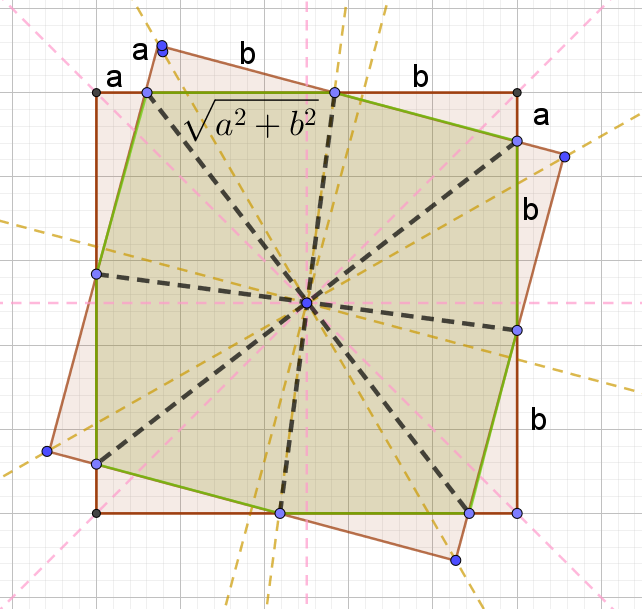
For starters why don't I say that the perimeter of the octagon is P units and work from there.
\(a+2b=1\\ a=1-2b\\~\\ 8\sqrt{a^2+b^2}=P\\ \sqrt{1+4b^2-4b+b^2}=\frac{P}{8}\\ \sqrt{5b^2-4b+1}=\frac{P}{8}\\ 5b^2-4b+1=\frac{P^2}{64}\\ 5b^2-4b+\frac{64-P^2}{64}=0\\ \triangle=16-\frac{20(64-P^2)}{64}\\ \triangle=\frac{16*64-20(64-P^2)}{64}\\ \triangle=\frac{4*64-5(64-P^2)}{16}\\ \triangle=\frac{-64+5P^2}{16}\\\)
There can be no real solution if the discriminant is negative so 5P^2 must be bigger or equal to 64
\(5P^2\ge64\\ P^2\ge12.8\\ P\ge \sqrt{12.8} \quad \text{which is approximately 3.5777} \)
So I am going to assume that the question intended the perimeter of the octagon to be sqrt(12.8)
which makes the discriminant 0
\(5b^2-4b+\frac{64-P^2}{64}=0\\ P=\sqrt{12.8}\\ b=\frac{4\pm0}{10}=\frac{2}{5}\\ a=1-2b=\frac{1}{5}\\ P=8\sqrt{\frac{1}{25}+\frac{4}{25}}=\sqrt{\frac{64*5}{25}}=\sqrt{12.8}\;\;\;\text{Excellent} \)
Area of the octogon = \(1- 4 * 0.5* a*b = 1-2*0.2*0.4 = 1-0.16 = 0.84 units^2\)
.