For problems like these, I like to use a table. I like to fill in the table with the information given to me and then create an equation that I can solve.
For this table, I will use the equation d=rt as the structure for the table.
| D | R | T | |
| Large Snowplow | |||
| Small Snowplow | |||
| Large Snowplow and Small Snowplow |
We will use the equation d=rt as a metaphor for this particular question.
d is metaphorical for the total amount done; for example, in this problem, the large snowplow is clearing one parking lot of its snow. Therefore, d=1 for the large snowplow.
Although we do not know how long the small snowplow takes to clear the parking lot yet, we do know that it has to clear one parking lot by itself, so d=1 for the small snowplow, as well.
When the snowplows work together, they both only clear one parking lot in this problem, so d=1 for the large and small snowplow. Let's fill this information in now.
| D | R | T | |
| Large Snowplow | 1p | ||
| Small Snowplow | 1p | ||
| Large Snowplow and Small Snowplow | 1p |
Next, I will fill in the "T" column, which represents time.
The given information states that the large snowplow leaves the parking lot devoid of snow after 4 hours. Therefore, t=4.
We do not know how much time it took the small snowplow to clear this parking lot; after all, that is what we are solving for. I will assign a variable, x, for that slot.
Collectively, the snowplows unload all that snow in a matter of 3 hours, so t=3 in the final row.
This is what the table looks like now:
| D | R | T | |
| Large Snowplow | 1p | 4hr | |
| Small Snowplow | 1p | xhr | |
| Large Snowplow and Small Snowplow | 1p | 3hr |
To fill in the rates, I will refer back to that metaphorical formula. I can rearrange this formula to solve for r.
| \(d=rt\) | divide by t to isolate r. |
| \(r=\frac{d}{t}\) |
This rearrangement shows that all I have to do is divide the "D" values by the "T" values in order to fill in the elements of the "R" column. Here is an update of what the table looks like.
| D | R | T | |
| Large Snowplow | \(1p\) | \(\frac{1p}{4\text{hr}}\) | \(4\text{hr}\) |
| Small Snowplow | \(1p\) | \(\frac{1p}{x\text{hr}}\) | \(x\text{hr}\) |
| Large Snowplow and Small Snowplow | \(1p\) | \(\frac{1p}{3\text{hr}}\) | \(3\text{hr}\) |
Great! We have the table filled out. In order to generate an equation, I want you to focus on the "R" column, the one that represents the rate of the snowplows. When the snowplows are in cahoots, their combined rates equal that of the sum of the individual rates. This allows us to generate an equation.
\(\frac{1}{4}+\frac{1}{x}=\frac{1}{3}\)
| \(\frac{1}{4}+\frac{1}{x}=\frac{1}{3}\) | There are many ways to approach this, but probably the simplest way is to multiply both sides by the LCD, 12x. |
| \(3x+12=4x\) | Subtract 3x on both sides. |
| \(x=12\text{hr.}\) | This is how long the small snowplow will take on its own. |
I think a diagram would allow you to visualize the problem.
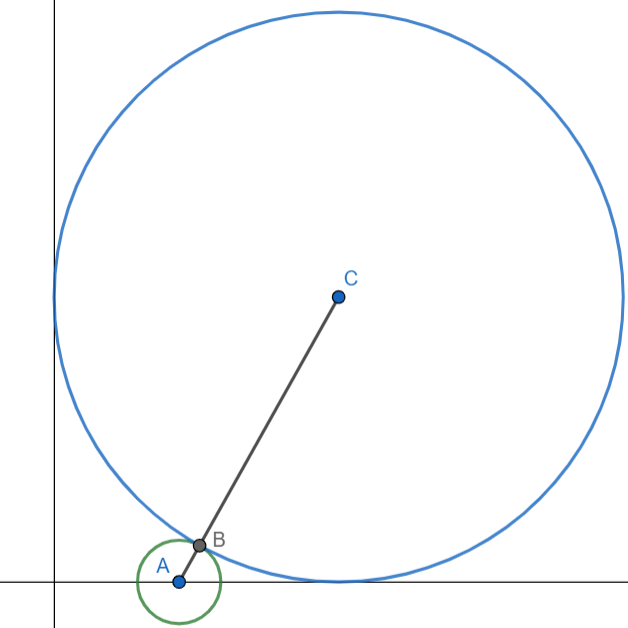
Let r equal the length of the radius of circle C.
The restrictions on circle C are such that the center is equidistant from both axes and lies in the first quadrant of the coordinate plane. I have defined the length of the radius to be r, so the center is r units away from both axes; therefore, the coordinates of the center are \((r,r)\) .
I am going to represent the distance from both centers in two different ways.
Since circle C and circle A are externally tangent, they intersect at only one common point. \(l_{\overline{BC}}=r\) because that segment is another radius, and all radii have the same length. \(l_{\overline{BA}}=1\) because the radius of circle A is given as 1.
\(l_{\overline{AC}}=l_{\overline{BC}}+l_{\overline{BA}}=r+1\)
\(r+1\) is the first way to represent the distance between the center of both circles. The second way requires the distance formula.
| \(\text{distance between }(r,r)\text{ and }(3,0);\\ d_{\overline{AC}}=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\) | (3,0) is the coordinate of the center of the circle A. (r,r) is the coordinate of the center of the circle C. |
| \(d_{\overline{AC}}=\sqrt{(r-3)^2+r^2}\) | This is the second way to represent the distance between the center of both circles. |
\(r+1\text{ and }\sqrt{(r-3)^2+r^2}\) represent the same idea: the distance between the center of both circles. This means that they are equal.
| \(\sqrt{(r-3)^2+r^2}=r+1\) | Before beginning to solve this problem, we must compute the domain restriction on this equality since a square root is present. |
| \((r-3)^2+r^2\geq 0\\ r^2-6r+9+r^2\geq 0\\ 2r^2-6r+9\geq 0\) | Expand this inequality fully on the left side. |
| \(a=2, b=-6, c=9\\ \Delta=b^2-4ac\\ \Delta=(-6)^2-4*2*9\\ \Delta=-36\\ ∴ \text{No restriction in domain}\\ D:(-\infty,\infty) \) | Delta represents the discriminant of this quadratic inequality. This quadratic has a positive leading coefficient, so the corresponding parabola faces upward in the coordinate plane. \(\Delta<0\), which means that this parabola never intersects the x-axis. The only way for both conditions to be true is that the parabola is forever above the x-axis, so the function will always output a value greater than zero. |
| \(\sqrt{(r-3)^2+r^2}=r+1\) | Solve for r by using algebraic manipulation. |
| \((r-3)^2+r^2=(r+1)^2\\ (r-3)^2+r^2-(r+1)^2=0\\ r^2-6r+9+r^2-(r^2+2r+1)=0\\ 2r^2-6r+9-r^2-2r-1=0\\ r^2-8r+8=0\) | Square both sides to eliminate the radical, bring all terms to the left-hand side of the equation, and simplify the left-hand side of the equation completely. This quadratic is not factorable, so we will have to resort to other methods to find the solutions. |
| \(a=1, b=-8, c=8\\ r_{1,2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\ r_{1,2}=\frac{-(-8)\pm\sqrt{(-8)^2-4*1*8}}{2*1}\\ r_{1,2}=\frac{8\pm\sqrt{32}}{2}\\ r_{1,2}=\frac{8\pm4\sqrt{2}}{2}\\ r_{1,2}=4\pm2\sqrt{2}\\ r_1=4+2\sqrt{2}\text{ or }r_2=4-2\sqrt{2}\) | Use the quadratic formula to determine both solutions. Both solutions are positive, so they are both valid for the context of this problem. |
| \(r_1+r_2\\ 4+2\sqrt{2}+4-2\sqrt{2}\\ 8\) | The sum of all possible radii is 8. |
This is how I would personally approach this problem.
#1: List all the integers from 1 to 100.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 |
| 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 |
| 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
#2: Eliminate all even numbers and 1 and 100 from the list since we are only interested in "square-free" numbers bounded between 1 and 100.
| 3 | 5 | 7 | 9 | ||||||
| 11 | 13 | 15 | 17 | 19 | |||||
| 21 | 23 | 25 | 27 | 29 | |||||
| 31 | 33 | 35 | 37 | 39 | |||||
| 41 | 43 | 45 | 47 | 49 | |||||
| 51 | 53 | 55 | 57 | 59 | |||||
| 61 | 63 | 65 | 67 | 69 | |||||
| 71 | 73 | 75 | 77 | 79 | |||||
| 81 | 83 | 85 | 87 | 89 | |||||
| 91 | 93 | 95 | 97 | 99 |
#3: Eliminate multiples of the first perfect square I will test, 3^2, or 9. I am not testing 2^2, or 4 because I have already eliminate the even numbers from the list, so no multiples of 4 remain in the list right now.
| 3 | 5 | 7 | |||||||
| 11 | 13 | 15 | 17 | 19 | |||||
| 21 | 23 | 25 | 29 | ||||||
| 31 | 33 | 35 | 37 | 39 | |||||
| 41 | 43 | 47 | 49 | ||||||
| 51 | 53 | 55 | 57 | 59 | |||||
| 61 | 65 | 67 | 69 | ||||||
| 71 | 73 | 75 | 77 | 79 | |||||
| 83 | 85 | 87 | 89 | ||||||
| 91 | 93 | 95 | 97 |
#4: Eliminate the multiples of the second perfect square I will test, 5^2, or 25. Again, I am not testing 4^2, or 16, because even numbers have already been filtered out.
| 3 | 5 | 7 | |||||||
| 11 | 13 | 15 | 17 | 19 | |||||
| 21 | 23 | 29 | |||||||
| 31 | 33 | 35 | 37 | 39 | |||||
| 41 | 43 | 47 | 49 | ||||||
| 51 | 53 | 55 | 57 | 59 | |||||
| 61 | 65 | 67 | 69 | ||||||
| 71 | 73 | 77 | 79 | ||||||
| 83 | 85 | 87 | 89 | ||||||
| 91 | 93 | 95 | 97 |
#5: Eliminate the multiples of 7^2, or 49. Only one number gets eliminated.
| 3 | 5 | 7 | |||||||
| 11 | 13 | 15 | 17 | 19 | |||||
| 21 | 23 | 29 | |||||||
| 31 | 33 | 35 | 37 | 39 | |||||
| 41 | 43 | 47 | |||||||
| 51 | 53 | 55 | 57 | 59 | |||||
| 61 | 65 | 67 | 69 | ||||||
| 71 | 73 | 77 | 79 | ||||||
| 83 | 85 | 87 | 89 | ||||||
| 91 | 93 | 95 | 97 |
#6: Normally, I would eliminate the multiples of 9^2, but I already sifted out the multiples of nine, so all the multiples of 9^2 have already been eliminated from the list.
#7: There is no need to eliminate the multiples of 11^2, or 121, since that multiple is larger than the largest number we are testing, so we can stop the process here. The numbers that remain are "square-free."
In a list, they are 3,5,7,11,13,15,17,19,21,23,29,31,33,35,37,39,41,43,47,51,53,55,57,59,61,65,67,69,71,73,77,79,83,85,87,89,91,93,95,97.
Since I was in the process of making this solution, I will post it. It is slightly different to Cphill's solution, but the concepts used are mostly the same.
Generating a diagram for problems for geometry is generally a useful strategy so that one can visualize the problem and make observations. Here is the diagram that I will reference throughout the solving process:
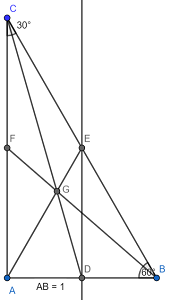
I have included all the given information and labeled extra points and lines because I plan to use them while solving.
\(\triangle ABC\) has a 30- and a 60-degree angle. The remaining angle of the triangle, \(m\angle CAB=90^{\circ}\) . The triangle is therefore classified as a 30-60-90 triangle.
30-60-90 triangles have a special property: their side lengths are always at a constant ratio of \(1:\sqrt{3}:2\) . Since I know the length of \(\overline{AB}\) , 1, I can determine the lengths of the others by setting up a proportion.
| \(\frac{AB}{BC}=\frac{1}{2}\) | This is the proportion that I mentioned earlier. |
| \(BC=2AB\) | I am solving for BC to make the proportion into a simple equation. Substitute 1 for AB. |
| \(BC=2\) | |
Now we know that BC=2. In order to go further with this solution, you must know what a centroid is. A centroid is a point of concurrency where all three medians of a triangle intersect in the interior of the triangle. This means you must know what a median is. A median of a triangle is a line segment joining a vertex to the midpoint of the opposite side of that vertex. This information will help us.
In the diagram above, \(\overline{AE}\) is a median. Therefore, point E is a midpoint of \(\overline{BC}\) , so point E bisects the segment. Therefore, \(BE=\frac{BC}{2}=\frac{2}{2}=1\) . This means that we have identified two side lengths and the measure of one angle of \(\triangle ABE\) . You may already recognize it based on the sides and the angles that the triangle is equilateral, but you can use the law of cosines to find \(AE\).
| \(c^2=a^2+b^2-2ab\cos C\) | c is the length that we are trying to find. a and b are the side lengths that we know already. |
| \(AE^2=AB^2+BE^2-2*AB*BE*\cos60^{\circ}\) | Substitute all the known values and solve for the remaining side length. |
| \(AE^2=1^2+1^2-2*1*1*0.5\) | Simplify the right-hand side. |
| \(AE^2=2-1=1\) | Take the square root of both sides. |
| \(AE=1\) | Of course, in the context of geometry, the negative answer is nonsensical, so we reject the answer. This is the length of the median. |
The centroid is located at point G, and there is one property about centroids that we must know in order to crack this one. It is that it divides the median into a ratio of 2:1. \(\overline{AG}\) is contained within \(\overline{AE}\), so we can generate a system of equations.
| \(\boxed{1}\frac{AG}{GE}=\frac{2}{1}\\ \boxed{2}AG+GE=AE=1\) | This is a system of equations that we can solve for AG. |
| \(AG=2GE\\ GE=\frac{AG}{2}\) | I manipulated the first equation and wrote in terms of GE. I will substitute this into the second equation to solve for AG. |
| \(AG+\frac{AG}{2}=1\) | Multiply by 2 on both sides to eliminate the fraction. |
| \(2AG+AG=2\) | Combine the like terms on the left-hand side of the equation. |
| \(3AG=2\) | Divide by 3 on both sides of the equation. |
| \(AG=\frac{2}{3}\) | |
... And finally, we are done!
I think the best thing to do here is to construct a diagram. The problem gives you vertices with coordinates from the Cartesian plane, and it even gives you an inequality. Here is the construction I created. I will reference it throughout the solving process:
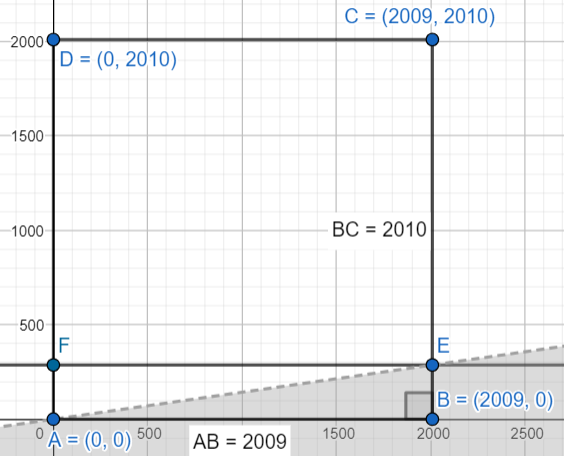
I first located the given coordinates and connected them with vertical and horizontal lines. I then graphed the inequality\(x>7y\), which can be rewritten as \(y<\frac{x}{7}\) . I added a few points, as they will become relevant when I solve.
One way to solve this problem is to figure out the ratio of the area created by the inequality \(y<\frac{x}{7}\) and the sides of the rectangle to the area of the entire rectangle. I will do this by first finding the coordinates of the point E. Point E is located on \(\overline{BC}\) , so its x-coordinate is also 2009. If you know the x-coordinate, then the y-coordinate of any point on \(y=\frac{x}{7}\) is \(\frac{x}{7}\) . Therefore, the y-coordinate is \(\frac{2009}{7}\) .
The formula for the area of the triangle is \(\frac{1}{2}bh\) . \(\triangle ABE\) is a right triangle, so the base and height are the side lengths that are not the hypotenuse. We know the length of the base, \(AB\) , because it is in the diagram. The height is the length of \(BE\) , or \(\frac{2009}{7}\)
\(A_{\triangle}=\frac{1}{2}*AB*BE=\frac{1}{2}*2009*\frac{2009}{7}=\frac{2009^2}{14}\)
We can also calculate the area of the rectangle
\(A_{\text{rect.}}=bh=AB*BC=2009*2010\)
As aforementioned, the probability of (x,y) such that x>7y is just the ratio of these areas.
| \(P(x,y|x>7y)=\frac{A_{\triangle}}{A_{\text{rect.}}}\) | As aforementioned, the probability of (x,y) such that x>7y is just the ratio of these areas. Substitute in the values and simplify. |
| \(P(x,y|x>7y)=\frac{\frac{2009^2}{14}}{2009*2010}\) | Use algebraic manipulation to simplify this. |
| \(P(x,y|x>7y)=\frac{2009^2}{14*2009*2010}\) | |
| \(P(x,y|x>7y)=\frac{2009}{14*2010}\) | At this point, you must use a calculator. |
| \(\)\(P(x,y|x>7y)=0.07139\) | |