TheXSquaredFactor

Let's first think of the domain of this particular function. 

The only portion of this function that can affect the state of the domain is the denominator, so let's investigate it. 

If there was a value for x such that \(|x-3|+|x+1|=0\), then a restriction for the domain of this function would exist. Let's see if there are any values for x such that this is true:

The nature of this function is generally one of a cubic function because there are no vertical asymptotes. Dividing by the addition of a sum of nonnegatives numbers does not really affect the range. 

\(\text{Range}: x \in {\rm I\!R}\)

For shirts, John has two options. He can either choose to wear the red shirt or the blue one. 

For pants, John has a total of three options. One pair of shorts, jeans, and slacks equals three options. 

The total number of combinations can be found by multiplying the number of independent options together. In this case, picking a shirt has no impact on which pair of pants John wears, so we can just multiply them together. 

\(2*3=6 \text{ shirt-and-pants combinations}\)

A box of cereal with dimensions 3in x 9in x 12in has a volume of 324in^3. The price of the box of cereal is $6. We can set up a proportion to determine the price per cubic inch:

\(\frac{\text{Price}}{\text{Cubic Inch}}=\frac{$6}{324in^3}=\frac{$1}{104in^3}\approx 0.00962\frac{\text{price}}{\text{in}^3}\)

A box of cereal with dimensions 2in x 8in x 9in has a volume of 104in^3. The price of the box is $4.50. Just like before, we can set up a proportion to determine the price per cubic inch:

\(\frac{\text{Price}}{\text{Cubic Inch}}=\frac{$4.50}{104\text{in}^3}=\frac{$9}{208\text{in}^3}\approx 0.04327\frac{\text{price}}{\text{in}^3}\)

Let's just find the difference of the simplified fractions of both boxes of cereal. 

\(\frac{9}{208}-\frac{1}{104}\\ \frac{9}{208}-\frac{2}{208}\\ \frac{7}{208}\approx0.03365\frac{\text{price}}{\text{in}^3}\)

PartialMathematician,

Yes, I believe you do have to sign up to share graphs with others. It is free.

I guess you could consider it to be a rationalization of the numerator.

I think that this question is fairly difficult. I have added a few extra lines and points to the diagram where I saw fit:

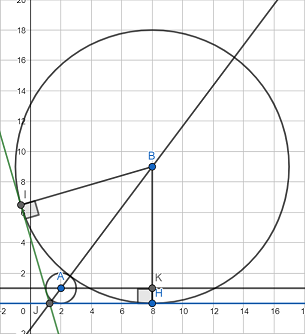
Here are my initial observations in regard to this current diagram:

• The x-axis, which is blue, is tangent to both circles.
• The green line is also tangent to both circles.
• The green and blue lines intersect at one common point on the x-axis. 

These initial observations are enough to get me started with this problem. I constructed a parallel line to the x-axis, \(\overleftrightarrow{AK}\). \(\angle BKA\) is, therefore, a right angle. Point K is located at (8,1) because it acquires the y-coordinate of Point A and the x-coordinate of Point B. \(\triangle BKA\) is a right triangle, and it is possible to find \(\tan(m\angle KAB)\). 

\(\tan m\angle KAB=\frac{9-1}{8-2}=\frac{8}{6}=\frac{4}{3}\). Notice how 4/3 is also the slope of  \(\overleftrightarrow{AB}\). The actual measure of the angle is not really important.

Because \(\overleftrightarrow{AK}||\overleftrightarrow{JH}\), \(\angle HJB\cong\angle KAB\). By extension, \(m\angle HJB=m\angle KAB\). This also means that \(\tan m\angle HJB=\tan m\angle KAB=\frac{4}{3}\). 

Because two tangent lines of a circle intersect at an external point, J, \(\angle IJB\cong\angle HJB\). Using the same reasoning as before, \(\tan m\angle IJB=\tan m\angle HJB=\frac{4}{3}\). \(m\angle IJH=m\angle IJB+m\angle HJB=m\angle HJB+m\angle HJB=2m\angle HJB\)

Both tangent lines meet at an angle of \(2m\angle HJB\). Just like finding \(\tan m\angle KAB\) yielded the slope, \(\tan 2m\angle HJB\) will yield the slope of the desired line, \(\overleftrightarrow{IJ}\). 

Luckily, we can utilize the Double-Angles Identities, specifically the \(\tan 2m\angle HJB=\frac{2\tan m\angle HJB}{1-\tan^2 m\angle HJB}\).

The equation of the circle with the center A is \((x-2)^2+(y-1)^2=1\). Since \(y=\frac{-24}{7}x+b\), substitute that into the equation for the circle:

The formula for the distance from a point to a line is \(d=\frac{|Ax+By+C|}{\sqrt{A^2+B^2}}\) when a line is written in the form \(Ax+By+C=0.\)

Cphill used the given equation for the line \(2x+y-5=0\). Therefore, \(A=2, B=1, \text{ and }C=-5\)

I do not want to confuse anyone more, but there are very specific circumstances where using a semicolon to separate items in a list is correct. This occurs when the items in the list contain commas already. This is not the case in OwenT154 question, though. Let's look at an example.

Look at the following list:

• New York
• California
• Nevada
• Florida

A sample sentence using these items is "I have been to New York, California, Nevada, and Florida."

Look at this modified list:

• New York, New York
• San Francisco, California
• Las Vegas, Nevada
• Miami, Florida

Notice how the items in the list already have commas. Therefore, semicolons are necessary to separate these items. A sample sentence using these items is "I have been to New York, New York; San Francisco, California; Las Vegas, Nevada; and Miami, Florida. For clarity purposes, commas are "promoted" to semicolons in order to show clear separation between each item.

Here is a simple scatter plot I made in Google Sheets. 

A)

B)

I do not see any areas that one can call a cluster. If you cannot identify any clusters or correlations in the graph, then there cannot be any outliers. 

The axis of symmetry can be found at \(x=\frac{-b}{2a}\), and we know that \(x=-3\), so \(\frac{-b}{2a}=-3\). We can now use algebraic manipulation to solve in terms of \(\frac{b}{a}\).

\(\frac{-b}{2a}=-3\\ \frac{b}{2a}=3\\ \frac{b}{a}=6\)