For the purposes of this problem, I will assume "when you are given one of the sides and an angle" means an angle other than the right angle. Another assumption I am making is that one of the given side lengths is not the hypotenuse as I doubt you would ask for the length of the hypotenuse if you already knew its side length. If these conditions are true, there are still 2 possibilities. I have created a diagram for both scenarios. Here they are:
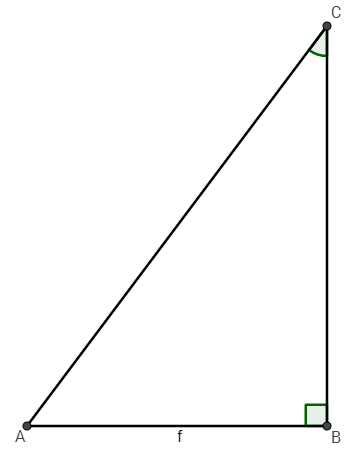
Let's assume that \(AB=6\) and \(m\angle C=35^{\circ}\). Now, let's "solve" the triangle. "Solving" the triangle means to figure out all the missing side lengths and angle measures. Let's start with the easy one first. You can use the triangle sum theorem to figure out what the measure of the angle located at vertex A:
| \(m\angle A+m\angle B+m\angle C=180\) | This is what the triangle sum theorem says; the sum of the measures of the angles in a triangle will equal 180 degrees. Now, plug in the angle measures that we already know. |
| \(m\angle A+90+35=180\) | Let's simplify the left-hand side of the equation by combining the like terms. |
| \(m\angle A+125=180\) | Finally, isolate the measure of angle a to figure out its exact measure. |
| \(m\angle A=55^{\circ}\) | |
The next part requires the knowledge of right-triangle trigonometry. Let's review that quickly. I understand that
\(\frac{\sin \textcolor{\green}\alpha}{1}=\frac{\textcolor{red}{\text{opposite}}}{\textcolor{blue}{\text{hypotenuse}}}\)
\(\frac{\cos \textcolor{green}{\alpha}}{1}=\frac{\textcolor{red}{\text{adjacent}}}{\textcolor{blue}{\text{hypotenuse}}}\)
\(\frac{\tan \textcolor{green}{\alpha}}{1}=\frac{\textcolor{red}{\text{opposite}}}{\textcolor{blue}{\text{adjacent}}}\)
Since we know that \(AB=6\) and \(m\angle C=35^{\circ}\), we should use the sine function to calculate the length of the hypotenuse and the tangent function for the angle adjacent to the known angle. Let's solve for the hypotenuse!
| \(\frac{\sin \textcolor{\green}\alpha}{1}=\frac{\textcolor{red}{\text{opposite}}}{\textcolor{blue}{\text{hypotenuse}}}\) | We know the measure of the angle, and we know the measure of the opposite side length. |
| \(\frac{\sin \textcolor{green}{35^{\circ}}}{1}=\frac{\textcolor{red}{\text{6}}}{\textcolor{blue}{\text{AC}}}\) | Multiply by the length of AC on both sides. |
| \(AC\sin 35^{\circ}=6\) | Now, divide by \(\sin 35^{\circ}\). |
| \(AC=\frac{6}{\sin 35^{\circ}}\) | \(\frac{6}{\sin 35^{\circ}}\) is the exact measure of the hypotenuse. By isolating its measure, we can now input it into a trusty scientific calculator (like the one provided on this Web site!) to obtain its approximate length. Be sure that the calculator is set to degree mode. |
| \(AC=\frac{6}{\sin 35^{\circ}}\approx10.46\) | Generally, rounding to the hundredths place is a sufficient estimation. |
Now, let's solve for the other side length. This time, we will need the tangent function.
| \(\frac{\tan \textcolor{green}{\alpha}}{1}=\frac{\textcolor{red}{\text{opposite}}}{\textcolor{blue}{\text{adjacent}}}\) | Let's do the exact same process of plugging in and isolating. |
| \(\frac{\tan \textcolor{green}{35^{\circ}}}{1}=\frac{\textcolor{red}{6}}{\textcolor{blue}{BC}}\) | |
| \(BC\tan 35^{\circ}=6\) | |
| \(BC=\frac{6}{\tan 35^{\circ}}\approx8.57\) | |
We have solved the triangle because we have found all the missing side lengths and angle measures. However, there is 1 scenario that we have not covered yet. However, the process is the same. Here is the diagram, with AB=5 and \(m\angle A=25^{\circ}\). You will notice that this is different that the first diagram.
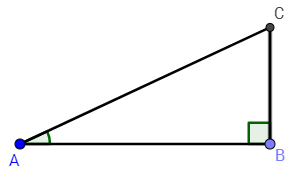
Let's find the easy one again: the measure of the angle of C:
| \(m\angle A+m\angle B+ m\angle C=180\) | |
| \(25+90+m\angle C=180\) | |
| \(115+m\angle B=180\) | |
| \(m\angle B=65^{\circ}\) | |
Oh wait! Now, this looks the exact same as the 1st triangle because we know the measure of the angle across from the known side length. Therefore, to solve this triangle, you would use the exact same process as done above.
The question asks for "80% of 55."
"Of" is an indicator for the multiplication indicator. You can replace it. We have now changed the question to \(80\% *55\). Now, let's evaluate it!
| \(80\% *55\) | In general, \(a\%=\frac{a}{100}\). |
| \(\frac{80}{100}*\frac{55}{1}\) | Let's simplify 80/100 to simplest terms by realizing that the numerator and denominator have a greatest common factor of 20. |
| \(\frac{4}{5}*\frac{55}{1}\) | To faciliate the computational process even more, notice that 5 and 55 havea GCF of 5. |
| \(\frac{4}{1}*\frac{11}{1}\) | Now, do the multiplication. |
| \(44\) | |
Therefore, 80% of 55 is 44.
Here's a diagram to reference as I solve. I made it myself.
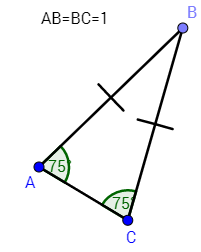
Despite that it is not noted on my diagram, \(m\angle B=30^{\circ}\), according to the given info. We already have enough information to solve for the area of the triangle.
In a triangle, if the length of 2 sides and measure of the included angle are known, then we can use the following formula to determine the area of the triangle. It is the following:
\(A_{\triangle}=\frac{1}{2}ab*\sin C\)
a = 1 side length of triangle
b = Another side length of the triangle
C = measure of the included angle
Now that we know this formula, just substitute into it.
| \(A_{\triangle}=\frac{1}{2}ab*\sin C\) | Plug in the appropriate values for a, b, and C. |
| \(A_{\triangle}=\frac{1}{2}*1*1*\sin (30)\) | You may have remembered that \(\sin(30)=\frac{1}{2}\). |
| \(A_{\triangle}=\frac{1}{2}*1*1*\frac{1}{2}\) | Of course, 1 mulriplied by a number is itself. |
| \(A_{\triangle}=\frac{1}{2}*\frac{1}{2}\) | Simplify this. |
| \(A_{\triangle}=\frac{1}{4}units^2=0.25units^2\) | Of course, do not forget to include the units! |
If I had to take a guess, I would say that one of the millennium prize problems set by the Clay Mathematics Institute at the beginning of the millennium. Only one has been solved thus far.
Out of those, the easiest to understand is P versus NP.
Click here to redirect yourself to the corresponding wikipedia page.
Before we start, let's define a few terms.
Odds is the ratio of the probability that an event can occur to the probability that an event cannot occur. Here is the formula in algabraic notation, if it makes it easier to understand.
\(\text{Odds}=\frac{p}{1-p}\)
p = probability
Probability is the ratio of the ways an event suits a condition to the number of possible outcomes.
\(p=\frac{\text{# of events}}{\text{# of outcomes}}\)
p = probability
Knowing this, we can answer all the questions up to 11.
8)
There are 3 primary colors in the colored cube, and this allows us to calculate the odds.
\(\text{Odds}=\frac{{\frac{1}{2}}}{1-\frac{1}{2}}=\frac{\frac{1}{2}}{\frac{1}{2}}=1:1\)
9)
Let's calculate the probability of not rolling a blue or purple. If we wanted to roll a blue or purple, the probability would be \(\frac{2}{6}=\frac{1}{3}\). The probability of that event not occuring is \(1-p\). Therefore, \(1-\frac{1}{3}=\frac{3}{3}-\frac{1}{3}=\frac{2}{3}\). Now, let's determine the odds.
| \(\text{Odds}=\frac{\frac{2}{3}}{1-\frac{2}{3}}\) | Simplify the denominator |
| \(1-\frac{2}{3}=\frac{3}{3}-\frac{2}{3}=\frac{1}{3}\) | |
| \(\text{Odds}=\frac{\frac{2}{3}}{\frac{1}{3}}\) | Multiply by \(\frac{3}{3}\) to eliminate the ugly denominator. |
| \(\text{Odds}=\frac{2}{3}*\frac{3}{1}=\frac{6}{3}=2:1\) | |
10)
There are 3 primary colors on the cube, which means that the probability is \(\frac{3}{6}=\frac{1}{2}\)
11) The probability of an event not occuring is represented by \(1-p\), so this means that \(1-\frac{1}{6}\) is the probability. Now, just simplify this.
\(1-\frac{1}{6}=\frac{6}{6}-\frac{5}{6}=\frac{1}{6}\)
.The equation graphed in the picture is not linear (because the graph is not a straight line). It is a quadratic, however, because it forms a parabola. I will use the quadratic in "vertex" form.
\(f(x)=a(x-h)^2+k\) where \((h,k)\) is the vertex.
However, we do not know what the value of a is. Therefore, I will resort to the "standard" quadratic form:
\(f(x)=ax^2+bx+c\)
Before we can identify the equation that contains this parabola, let's see if we can determine the y-intercept. It would appear as if it is located at (0,4). Let's plug that in.
| \(f(x)=ax^2+bx+c\) | Plug this in when x=0. |
| \(f(0)=a(0)^2=b*0+c\) | Of course, the 0's make simplification much easier. |
| \(f(0)=c\) | Now, we know what \(f(0)\) equals because we know the corresponding y-coordinate when x=0. It happens to be 4. |
| \(4=c\) | |
Now, let's use another point. This time, I will use the vertex, which appears to be located at (2,0). Let's do the exact same process.
| \(f(x)=ax^2+bx+c\) | Replace every instance of x with 2, in this case, as that is the x-coordinate we want. |
| \(f(2)=a(2)^2+b*2+c\) | Let's simplify the right hand side. |
| \(f(2)=4a+2b+ c\) | Of course, we know that \(f(2)=0\). |
| \(0=4a+2b+c\) | |
We need 1 more point. For a quadratic, you always need 3 points to determine its equation. Because quadratic equations have symmetry along its axis of symmetry, we know that (4,4) is also a point on the parabola. Let's plug that in, and we will utilize the exact same process.
| \(f(4)=a(4)^2+b*4+c\) | Yet again, simplify the right hand side. |
| \(f(4)=16a+4b+c\) | We know that \(f(4)=4\), so plug that in. |
| \(4=16a+4b+c\) | |
Great! Let's look at these equations side-by-side:
{ \(4=c\)
{ \(0=4a+2b+c\)
{ \(4=16a+4b+c\)
Of course, if 4=c, then we can make this look a tad nicer:
{ \(0=4a+2b+4\)
{ \(4=16a+4b+4\)
Let's make it nicer again! To make it easier, the first equation has a GCF of 2, and the second equation has a GCF of 4. Simplifying this will make the numbers in our system of equations smaller and easier to work with.
{ \(0=2a+b+2\)
{ \(1=4a+b+1\)
Now, let's solve this system of equations! I will use the substitution method because it is easier to understand when I write. I'll use the first equation first. My goal here is to isolate a variable. Since b has a coefficient of 1 already, I think I will isolate that variable.
| \(0=2a+b+2\) | Subtract b on both sides. |
| \(-b=2a+2\) | Divide by -1 on both sides to isolate b. |
| \(b=-2a-2\) | |
Plug this into b for equation 2:
| \(1=4a+b+1\) | Since \(b=-2a-2\) according to our previous equation, plug that in. |
| \(1=4a+(-2a-2)+1\) | Simplify the right hand side of the equation. The parentheses aren't actually necessary, but it might make it clearer where the substitution is taking place. |
| \(1=2a-1\) | Add 1 to both sides. |
| \(2=2a\) | Divide by 2 on both sides to isolate a. |
| \(a=1\) | |
Great! We know that a=1. We actually need not solve for b, in this case, as we know what the vertex is already, and we can use vertex form. As a recap, "vertex" form is the following:
\(f(x)=a(x-h)^2+k\) where (h,k) is the vertex
Well, a=1, and the vertex is (2,0). Plug that in.
\(f(x)=1(x-2)^2+0\)
This can be simplified.
\(f(x)=(x-2)^2\)
This means that a=1, h=2, and k=0. I hope this helps!
Here, I'm ready to help!
| \(12*4\frac{1}{2}\) | Convert the mixed number into an improper fraction. |
| \(4\frac{1}{2}=\frac{2*4+1}{2}=\frac{9}{2}\) | Plug this back into the expression. |
| \(\frac{12}{1}*\frac{9}{2}\) | 12 and 2 have a GCF of 2, so we can factor that out to facilitate the computation. |
| \(\frac{6}{1}*\frac{9}{1}\) | This is much easier, dont you think? Now, multiply the fractions together. |
| \(54\) | |
Therefore, \(12*4\frac{1}{2}=54\)
.