CalculatorUser

Dont be intimidated! You don't even need to figure out the exact angle measures of ABC and ACB! Just find the sum of their angle measures. (You may need to scroll horizontally)

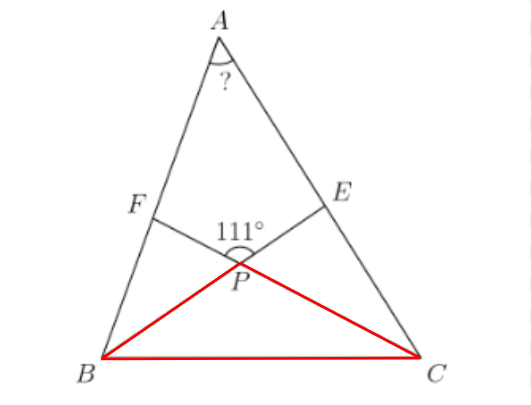
\(\text{Triangle ABC's angles add up to 180. And since angle ABC and ACB are bisected. We can assign them values }\frac{1}{2}x\text{ and }\frac{1}{2}y\)

\(\text{We draw triangle PBC as shown in the image in red}\)

\(\text{Due to the Vertical Angle Theorem, angle P in triangle PBC is 111}\)

\(\text{Since the angle measures of PBC sum up to 180. We can make the following equation}\)

\(\frac{1}{2}x+\frac{1}{2}y+111=180\)

\(\text{Now we solve the equation for x + y and get }x+y=138\)

\(\text{We solved for x + y, this means we just solved for the SUM of the angle measures of ABC and ACB}\)

\(\text{Since the angle measures of triangle ABC sum up to 180, and we know that the sum of two angles is 138.}\)

\(\text{We can figure out the third angle with the following equation. }128 + n = 180\rightarrow{n}=\boxed{42}\)

where is the picture? 

SO much information is missing!

Credit to Cphill for answer

1. the range of x is going to be like a ray, with a end point while goes to infinity in another direction.

\(f(x)=\sqrt{{\color{red}3}x+{\color{red}6}}-7\)

You do \((-1)*\frac{{\color{red}6}}{{\color{red}3}}\Rightarrow-2\)

This means the minimum of x is -2, while the maximum goes to infinity.

I couldn't solve it, but I can get you started on this problem

After thinking of this for an eternity, I only came up with that the largest triangle you can make into a circle is an inscribed equilateral triangle with points XYZ.

So

If you have that inscribed equilateral triangle XYZ that is inscribed in a circle

to fit into the restrictions of the problem.

you will have to deform the equilateral triangle to do so.

You have to have vertice X as close to A (vertice of square) as possible this makes A your new point on of the triangle instead of X. Then you have to make sure vertices Y and Z are collinear with C (vertice of square)

Y and Z have to be as far as apart as possible while it has to be as close to edge CD of square as possible while remaining in circle w.

That was with my imagination, I am not sure if this is entirely correct.

Thank you, thats similar what my math teacher said! 

Yes, CPhill's solution is also a way to get the answer!

thanks!

\(\text{Because angle TRS is 55, that means angle QRT is 125}\)

\(\text{We construct a line from Point R to our new point X. Let segment RX be parallel to QP and TU.}\)

\(\text{Angle PQR and angle QRX add up to 180. This means QRX must be 60}\)

\(\text{If angle QRT is 125 and angle QRX is 60, this means angle RTU is 65}\)

\(\text{Angle XRT and angle RTU sum up to 180. And since RTU is 65, this means angle RTU is }\boxed{115^{\circ}}\)

\(\text{We can draw a line from point B to point D to create triangle BCD}\)

\(\text{Notice how angle FBD is 90 degrees with angle FBC of 125 degrees. This means angle DBC is 35 degrees.}\)

\(\text{Since the sum of the angles of a triangle is 180, this means angle BDC is 55 degrees}\)

\(\text{Now notice how angle BDE is 90 degrees, and we have angle BDC is 55 degrees. That means angle x is }\boxed{35^{\circ}}\)