heureka

Three concentric circles are drawn such that the area of the smallest circle is equal to the area of each of the rings.
If the radius of the largest circle is 12 cm,
what is the radius of the smallest circle?

\(\begin{array}{rcll} \text{Let smallest circle radius $=r_s$ } \\ \text{Let middle circle radius $=r_m$ }\\ \text{Let largest circle radius $=r_l$ }\\ \end{array} \)

\(\begin{array}{|lrcll|} \hline & \pi r_s^2 = \pi r_m^2-\pi r_s^2 = \pi r_l^2 - \pi r_m^2 \quad & | \quad : \pi \\ & r_s^2 = r_m^2- r_s^2 = r_l^2- r_m^2 \\ \hline \end{array} \)

\(\begin{array}{lrcll} (1) & 2r_s^2 &=& r_m^2 \\ \hline (2) & 2r_m^2 &=& r_l^2 + r_s^2 \quad & | \quad r_m^2 = 2r_s^2 \\ & 2\cdot (2r_s^2) &=& r_l^2 + r_s^2 \\ & 4r_s^2 &=& r_l^2 + r_s^2 \\ & 3r_s^2 &=& r_l^2 \quad & | \quad \sqrt{ }\\ & \sqrt{3}r_s &=& r_l \quad & | \quad r_l = 12 \\ & \sqrt{3}r_s &=& 12 \\ & r_s &=& \dfrac{12}{\sqrt{3}} \\ & r_s &=& \dfrac{12 \sqrt{3}}{\sqrt{3}\sqrt{3}} \\ & r_s &=& \dfrac{12 \sqrt{3}}{3} \\ & \mathbf{r_s} &\mathbf{=}& \mathbf{4 \sqrt{3} } \\ \end{array}\)

\(\text{The radius of the smallest circle is $\mathbf{4 \sqrt{3} }$ cm $\approx \mathbf{6.9} $ cm } \)

correction and the sum:

Thank you very much, Melody.

Hallo,

ich benötige Hilfe bei der folgenden Aufgabe:

Bestimmen Sie alle Vektoren, die sowohl zum Vektor a=(1 0 4) als auch zum Vektor b = (4 -1 2) orthogonal sind.

\(\begin{array}{|rcll|} \hline \vec{v_\bot} &=& \begin{pmatrix} 1 \\ 0 \\ 4 \end {pmatrix} \times \begin{pmatrix} 4 \\ -1 \\ 2 \end {pmatrix} \quad & | \quad \text{Vektor Kreuzprodukt} \\\\ &=& \begin{vmatrix} 1 & 1 & 1 \\ 1 & 0 & 4 \\ 4 & -1 & 2 \end {vmatrix} \quad & | \quad \text{Determinante} \\\\ &=& \begin{pmatrix} \begin{vmatrix} 0 & 4 \\ -1 & 2 \end {vmatrix} \\ -\begin{vmatrix} 1& 4 \\ 4 & 2 \end {vmatrix} \\ \begin{vmatrix} 1 & 0 \\ 4 & -1 \end {vmatrix} \end {pmatrix} \\\\ &=& \begin{pmatrix} 0\cdot 2-(-1)\cdot 4 \\ -(2-16) \\ 1(-1)-4\cdot 0 \end {pmatrix} \\\\ \mathbf{ \vec{{v_1}_\bot} }&\mathbf{=}& \mathbf{ \begin{pmatrix} 4 \\ 14 \\ -1 \end {pmatrix} }\quad & | \quad \text{1. Lösung} \\\\ \vec{{v_2}_\bot}&=& -\vec{{v_1}_\bot} \\\\ \vec{{v_2}_\bot}&=& -\begin{pmatrix} 4 \\ 14 \\ -1 \end {pmatrix} \\\\ \mathbf{ \vec{{v_2}_\bot} }&\mathbf{=}&\mathbf{ \begin{pmatrix} -4 \\ -14 \\ 1 \end {pmatrix} } \quad & | \quad \text{2. Lösung, kollineare Vektor} \\ \hline \end{array} \)

Hi Melody,

Your question is, "I will admit that I do not understand the second half of what you have done though Heureka. 

How did that combinatory maths sneak in there?"

1. The formula is from Jacob Bernoulli. Sorry the original paper from Jacob Bernoulli, Ars conjectandi ( Wahrscheinlichkeitsrechnung) page 100 is in german.

 If $f$ is a polynomial of degree $4$ such that $$f(0) = f(1) = f(2) = f(3) = 1$$ and $$f(4) = 0,$$ then determine $f(5)$.

\(\small{ \begin{array}{lrrrrrrrrrrrrr} & f(0) && f(1) && f(2) && f(3) && f(4) && {\color{red}f(5)} && \cdots \\ & d_0=1 && 1 && 1 && 1 && 0 && {\color{red}-4} && \cdots \\ \text{1. Difference } && d_1=0 && 0 && 0 && -1 && {\color{red}-4} && \cdots \\ \text{2. Difference } &&& d_2=0 && 0 && -1 && {\color{red}-3} && \cdots \\ \text{3. Difference } &&&& d_3=0 && -1 && {\color{red}-2} && \cdots \\ \text{4. Difference } &&&&& {\color{red}d_4=-1 } && {\color{red}-1} && \cdots \\ \end{array} }\)

\(\text{ ${\color{red}d_4=-1}$ is constant, if a polynomial is of degree 4.} \)

\(f(5) = {\color{red}-1}+(-1)+(-1)+(-1)+0 = -4\)

polynomial:

\(\small{ \begin{array}{rcll} \hline a_n &=& \binom{n-1}{0}\cdot {\color{red}d_0 } + \binom{n-1}{1}\cdot {\color{red}d_1 } + \binom{n-1}{2}\cdot {\color{red}d_2 } + \binom{n-1}{3}\cdot {\color{red}d_3 } + \binom{n-1}{4}\cdot {\color{red}d_4 } \\\\ && \quad {\color{red}d_0 } = 1 \quad {\color{red}d_1}={\color{red}d_2}={\color{red}d_3} = 0 \quad {\color{red}d_4 } = -1 \\\\ a_n &=& \binom{n-1}{0}\cdot 1 + \binom{n-1}{1}\cdot 0 + \binom{n-1}{2}\cdot 0 + \binom{n-1}{3}\cdot 0 + \binom{n-1}{4}\cdot (-1) \\ a_n &=& \binom{n-1}{0}\cdot 1 - \binom{n-1}{4} \quad & | \quad \binom{n-1}{0} = 1 \\ a_n &=& 1 - \dbinom{n-1}{4} \quad & | \quad n = x+1 \\ \mathbf{f(x)} &\mathbf{=}& \mathbf{ 1 - \binom{x}{4} } \\\\ && \quad \dbinom{x}{4} = \left(\dfrac{x}{4}\right)\left(\dfrac{x-1}{3}\right)\left(\dfrac{x-2}{2}\right)\left(\dfrac{x-3}{1}\right) \\\\ \mathbf{f(x)} &\mathbf{=}& \mathbf{ 1 - \dfrac{x(x-1)(x-2)(x-3)}{24} } \\ \end{array} } \)

Thank you Guest

Coordinates plane H(-5,-6) & J(5,-1).
Find the Point Q that is 4/5 the distance from J to H

Formula:

\(\begin{array}{|rcll|} \hline \mathbf{\vec{Q}} &\mathbf{=}& \mathbf{(1-\lambda)\vec{J} + \lambda\vec{H}} \quad & | \quad\lambda = \dfrac45 \\\\ \vec{Q} &=& \left(1-\dfrac45 \right)\vec{J} + \dfrac45\cdot \vec{H} \\\\ &=& \dfrac15 \vec{J} + \dfrac45 \vec{H} \quad & | \quad \vec{J} = \dbinom{5}{-1} \quad \vec{H} = \dbinom{-5}{-6} \\\\ &=& \dfrac15 \dbinom{5}{-1} + \dfrac45 \dbinom{-5}{-6} \\\\ &=& \dbinom{1}{-\dfrac15} + \dbinom{-4}{-\dfrac{24}{5}} \\\\ &=& \dbinom{1}{-\dfrac15} - \dbinom{4}{\dfrac{24}{5}} \\\\ &=& \dbinom{1-4}{-\dfrac15-\dfrac{24}{5 }} \\\\ &=& \dbinom{-3}{-\dfrac{25}{5 }} \\\\ \mathbf{\vec{Q}} & \mathbf{=}& \mathbf{\dbinom{-3}{-5}} \\ \hline \end{array}\)

point A is located at (1,4). Point P ar (3,5) is 1/3 the distance from A to point B.

What are the coordinates of point b (SHOW WORK)

Formula:

\(\begin{array}{|l|rcll|} \hline & \mathbf{(1-\lambda)\vec{A} + \lambda\vec{B}} &\mathbf{=}& \mathbf{\vec{P}} \\ \hline \lambda = 0 & (1-0)\vec{A} + 0\cdot \vec{B} &=& \vec{A} \ \checkmark \\\\ \lambda = 1 & (1-1)\vec{A} + 1\cdot \vec{B} &=& \vec{B} \ \checkmark \\\\ \lambda = \dfrac13 & \left(1-\dfrac13 \right)\vec{A} + \dfrac13\cdot \vec{B} &=& \vec{P} \quad & | \quad \vec{B} =\ ? \\ \hline \end{array}\)

\(\vec{B} =\ ?\)

\(\begin{array}{|rcll|} \hline \left(1-\dfrac13 \right)\vec{A} + \dfrac13\cdot \vec{B} &=& \vec{P} \quad & | \quad \vec{B} =\ ? \\\\ \dfrac23 \vec{A} + \dfrac13 \vec{B} &=& \vec{P} \quad & | \quad \cdot 3 \\ \\ 2 \vec{A} + \vec{B} &=& 3 \vec{P} \quad & | \quad - 2 \vec{A} \\\\ \mathbf{\vec{B}} &\mathbf{=}& \mathbf{3 \vec{P} - 2 \vec{A}}\quad & | \quad \vec{A} = \binom{1}{4} \quad \vec{P} = \binom{3}{5} \\\\ \vec{B} &=& 3\binom{3}{5} - 2 \binom{1}{4} \\\\ \vec{B} &=& \binom{9}{15} - \binom{2}{8} \\\\ \vec{B} &=& \binom{9-2}{15-8} \\\\ \mathbf{\vec{B}} &\mathbf{=}& \mathbf{\binom{7}{7}} \\ \hline \end{array}\)

What is the smallest positive integer N  for which

\((12{,}500{,}000)\cdot n\) 

leaves a remainder of 111 when divided by 999,999,999?

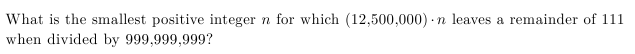
1.

\(\begin{array}{|rcll|} \hline (12~500~000)\cdot n & \equiv & 111 \pmod{999~999~999} \quad & | \quad :(12~500~000) \\ n & \equiv & 111\cdot \dfrac{1}{12~500~000} \pmod{999~999~999} \\ \hline \end{array}\)

\(\begin{array}{|lcll|} \hline \text{According to Euler's theorem,} \\ \text{if $a$ is coprime to $m$, that is, $gcd(a, m) = 1$, then }\\ {\displaystyle a^{\phi (m)}\equiv 1{\pmod {m}},}\\ \text{where ${\displaystyle \phi } $ is Euler's totient function.}\\ \text{Therefore, a modular multiplicative inverse can be found directly:} \\ {\displaystyle a^{\phi (m)-1}\equiv a^{-1}{\pmod {m}}.} \\ \hline \end{array}\)

2.

\(\text{greatest common divisor $gcd(12~500~000,999~999~999) = 1$ }\)

\(\begin{array}{|rcll|} \hline && \dfrac{1}{12~500~000} \pmod{999~999~999} \\\\ & \mathbf{\equiv} & \mathbf{12~500~000^{-1} \pmod{999~999~999}} \\\\ & \equiv & 12~500~000^{\phi (999~999~999)-1} \pmod{999~999~999} \\\\ & \equiv & 12~500~000^{648~646~704-1} \pmod{999~999~999} \\\\ & \equiv & 12~500~000^{648~646~703} \pmod{999~999~999} \\\\ & \mathbf{\equiv} & \mathbf{80 \pmod{999~999~999}} \\ \hline \end{array}\)

3. n = ?

\(\begin{array}{|rcll|} \hline n & \equiv & 111\cdot \dfrac{1}{12~500~000} \pmod{999~999~999} \\\\ & \equiv & 111\cdot \left( 12~500~000^{-1} \pmod{999~999~999} \right) \\\\ & \equiv & 111\cdot 80 \pmod{999~999~999} \\\\ & \mathbf{\equiv} & \mathbf{ 8880 \pmod{999~999~999} } \\ \hline \end{array}\)

The smallest positive integer n is 8880.

\(\begin{array}{rcll} 12 ~500~000 \cdot 8880 &\equiv & 111 \pmod{999~999~999} \\ 110~000~000~000 &\equiv & 111 \pmod{999~999~999}\ \checkmark\\ \end{array}\)
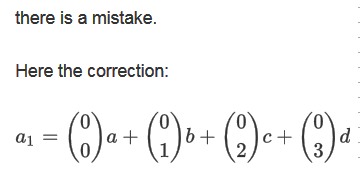