heureka

A ball travels on a parabolic path in which the height (in feet) is given by the expression $-16t^2+80t+21$,
where $t$ is the time after launch.
What is the maximum height of the ball?

The graph:

\(\begin{array}{|lrcll|} \hline & h(t) &=& -16t^2+80t+21 \\ h = 0 \ ? \\ & -16t^2+80t+21 &=& 0 \\\\ & t_{1,2} &=& \dfrac{-80 \pm\sqrt{80^2-4\cdot(-16)\cdot21}}{2\cdot(-16)} \\\\ & &=& \dfrac{-80 \pm\sqrt{6400+1344} }{-32} \\\\ & t_{1,2} &=& \dfrac{-80 \pm88}{-32} \\\\ & t_1 &=& \dfrac{-80 + 88}{-32} \\\\ & &=& \dfrac{8}{-32} \\\\ & \mathbf{t_1} &\mathbf{=}& \mathbf{-0.25} \\\\ & t_2 &=& \dfrac{-80 - 88}{-32} \\\\ & &=& \dfrac{168}{32} \\\\ & \mathbf{t_2} &\mathbf{=}& \mathbf{5.25} \\\\ &t_{h_\text{max}} &=& \dfrac{t_1+t_2}{2} \\\\ & &=& \dfrac{-0.25+5.25}{2} \\\\ & &=& \dfrac{5}{2} \\\\ &\mathbf{t_{h_\text{max}}} &\mathbf{=}& \mathbf{2.5} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline h_\text{max} &=& -16\mathbf{t_{h_\text{max}}}^2+80\mathbf{t_{h_\text{max}}}+21 \quad & | \quad \mathbf{t_{h_\text{max}} = 2.5} \\ &=& -16\cdot 2.5^2+80\cdot 2.5+21 \\ &=& -100+200+21 \\ &\mathbf{=}& \mathbf{121~ \text{feet}}\\ \hline \end{array}\)

The maximum height of the ball is \( \mathbf{121~ \text{feet}}\)

Larry has 4-cent stamps and 9-cent stamps, which he can combine to produce various amounts of postage.
For example, he can make 40 cents by using four 9-cent stamps and a 4-cent stamp, or by using ten 4-cent stamps.
However, there are some amounts of postage he can't make exactly, such as 10 cents.

What is the largest number of cents that Larry CANNOT make exactly from a combination of 4- and/or 9-cent stamps?

Explain how you know your answer is correct. (You should explain two things:
why Larry can't make the amount of your answer, and
why he CAN make any bigger amount.)

\(\begin{array}{l} \cdots\{4\} \cdots \{8,9\}\cdots \{12,13\}\cdots \{16,17,18\} \cdots \{20,21,22\} \cdots {\color{red}23} \{\underbrace{24,25,26,27}_{\underset{27+4=31}{\underset{26+4=30,}{\underset{25+4=29,}{\underset{24+4=28,}{}}}} }\} \{\underbrace{28,29,30,31}_{\underset{31+4=35}{\underset{30+4=34,}{\underset{29+4=23,}{\underset{28+4=32,}{}}}} }\} \{\underbrace{32,33,34,35}_{\underset{35+4=39}{\underset{34+4=38,}{\underset{33+4=37,}{\underset{32+4=36,}{}}}} }\} \text{ and so on} \\\\ \{\text{reachable}\} \\ \cdots \text{not reachable}\\ \end{array} \)

23 is the largest number of cents that Larry CANNOT make exactly from a combination of 4- and/or 9-cent stamps.

After four consecutive reachable numbers, 24, 25, 26, 27, he CAN make any bigger amount.

If c is a constant such that 9x^2 + 10x + c is equal to the square of a binomial, then what is c?

\(\begin{array}{|lrcll|} \hline &(9x^2+10x+c) &=& (3x+b)^2 \\ & &=& 9x^2+\underbrace{6b}_{=10}x+\underbrace{b^2}_{=c} \\\\ \hline (1) & 6b &=& 10 \\ & b &=& \frac53 \\\\ (2) & c &=& b^2 \\ & c &=& (\frac53)^2 \\ & c &=& \frac{25}{9} \\ \hline &\left(9x^2+10x+\dfrac{25}{9} \right) &=& \left(3x+\dfrac53 \right)^2 \\ \hline \end{array}\)

Graph the image of the figure after a dilation with a scale factor of 2 centered at (−2, −2) .

\(\begin{array}{lrcll} \text{Formula dilation:} & \boxed{\vec{A}' = (\vec{A}-\vec{C_{Center}})\cdot \lambda +\vec{C_{Center}}} \\ & \vec{A} \text{ before dilation } & \text{$\lambda$ scale factor } = 2 \\ & \vec{A}' \text{ after dilation } & \text{$\vec{C_{Center}}$ center at $\binom{-2}{-2} $ } \\ \end{array} \)

\(\begin{array}{lrcll} &\vec{A}' &=& (\vec{A}-\vec{C_{Center}})\cdot \lambda +\vec{C_{Center}}\\ & &=& \vec{A}\cdot \lambda +\vec{C_{Center}}\cdot (1-\lambda ) \\ & &=& \lambda \cdot \vec{A} +(1-\lambda )\cdot \vec{C_{Center}} \\ \text{Formula dilation:} & \boxed{\vec{A}' =\lambda \cdot \vec{A} +(1-\lambda )\cdot \vec{C_{Center}}} \\ & (1-\lambda )\cdot \vec{C_{Center}} &=& (1-2)\binom{-2}{-2} \\ & (1-\lambda )\cdot \vec{C_{Center}} &=& (-1)\binom{-2}{-2} \\ & (1-\lambda )\cdot \vec{C_{Center}} &=& \binom{2}{2} \\ \end{array}\)

\(\begin{array}{lrcll} \boxed{\vec{A}'=\lambda \cdot \vec{A} +\binom{2}{2}}& \vec{A} = \dbinom{-4}{-2}\\ \boxed{\vec{B}'=\lambda \cdot \vec{B} +\binom{2}{2}}& \vec{B} = \dbinom{-5}{2}\\ \boxed{\vec{C}'=\lambda \cdot \vec{C} +\binom{2}{2}}& \vec{C} = \dbinom{-1}{3}\\ \boxed{\vec{D}'=\lambda \cdot \vec{D} +\binom{2}{2}}& \vec{D}= \dbinom{1}{1}\\ \end{array}\)

\(\begin{array}{lrcll} \boxed{\vec{A}'=2 \cdot \binom{-4}{-2} +\binom{2}{2}}& \vec{A}' = \dbinom{-6}{-2}\\ \boxed{\vec{B}'=2 \cdot \binom{-5}{2} +\binom{2}{2}}& \vec{B}' = \dbinom{-8}{6}\\ \boxed{\vec{C}'=2 \cdot \binom{-1}{3} +\binom{2}{2}}& \vec{C}' = \dbinom{0}{8}\\ \boxed{\vec{D}'=2 \cdot \binom{1}{1} +\binom{2}{2}}& \vec{D}' = \dbinom{4}{4}\\ \end{array} \)

Point (-4, -2 ) goes to (-6,-2)

Point (-5, 2) goes to (-8. 6)

Point ( -1, 3) goes to (0, 8)

Point ( 1, 1 ) goes to (4, 4 )

Find all real x that satisfy (2^x - 4)^3 + (4^x - 2)^3 = (4^x + 2^x - 6)^3

\(\begin{array}{|lrcll|} \hline (2^x - 4)^3 + (4^x - 2)^3 = (4^x + 2^x - 6)^3 \\ \qquad\text{We substitute:} ~ a = 2^x,~ b = 4^x,~ c = -4,~ d = -2 \\ (a +c)^3 + (b +d)^3 = (a+b+c+d)^3 \\ \hline \end{array}\\ \small{ \begin{array}{|lrcll|} \hline a^3+3ac(a+c)+c^3+b^3+3bd(b+d)+d^3 & =& a^3 + b^3 + c^3+ d^3 \\ && + 6 a b c + 6 a b d + 6 a c d + 6 b c d \\ & & + 3 a^2 b + 3 a^2 c + 3 a^2 d + 3 a b^2 \\ & & + 3 a c^2 + 3 a d^2 + 3 b^2 c + 3 b^2 d \\ & & + 3 b c^2 + 3 b d^2 + 3 c^2 d + 3 c d^2 \\ \not{a^3}+\not{b^3}+\not{c^3}+\not{d^3}+\not{3a^2c}+\not{3ac^2}+\not{3b^2d}+\not{3bd^2} & =& \not{a^3} + \not{b^3} + \not{c^3}+ \not{d^3} \\ && + 6 a b c + 6 a b d + 6 a c d + 6 b c d \\ & & + 3 a^2 b + \not{3 a^2 c} + 3 a^2 d + 3 a b^2 \\ & & + \not{3 a c^2} + 3 a d^2 + 3 b^2 c + \not{3 b^2 d} \\ & & + 3 b c^2 + \not{3 b d^2} + 3 c^2 d + 3 c d^2 \\ \hline \end{array}}\\ \small{ \begin{array}{|rcll|} \hline 0 &=& 6 a b c + 6 a b d + 6 a c d + 6 b c d + 3 a^2 b + 3 a^2 d + 3 a b^2 + 3 a d^2 + 3 b^2 c + 3 b c^2 + 3 c^2 d + 3 c d^2 ~ | ~: 3 \\ 0 &=& 2 a b c + 2 a b d + 2 a c d + 2 b c d + a^2 b + a^2 d + a b^2 + a d^2 + b^2 c + b c^2 + c^2 d + c d^2 \\ 0 &=& a^2(b+d)+b^2(a+c)+c^2(b+d)+d^2(a+c)+2bd(a+c)+2ac(b+d) \\ 0 &=& (b+d)(a^2+2ac+c^2)+(a+c)(b^2+bd+d^2) \\ 0 &=& (b+d)(a+c)^2+(a+c)(b+d)^2 \\ 0 &=& (b+d)(a+c)(a+b+c+d) \\ \hline \end{array}}\)

Solution:

\(\begin{array}{|rcll|} \hline \mathbf{b+d} &\mathbf{=}& \mathbf{0} \\ 4^x-2 &=& 0 \\ 4^x &=& 2 \\ 2^{2x} &=& 2^1 \\ 2x &=& 1 \\ \mathbf{x_1} &\mathbf{=}& \mathbf{\dfrac{1}{2}} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \mathbf{a+c} &\mathbf{=}& \mathbf{0} \\ 2^x-4 &=& 0 \\ 2^x &=& 4 \\ 2^{x} &=& 2^2 \\ x &=& 2 \\ \mathbf{x_2} &\mathbf{=}& \mathbf{2} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \mathbf{a+b+c+d} &\mathbf{=}& \mathbf{0} \\ 2^x + 4^x-6 &=& 0 \\ (2^x-2)(2^x+3) &=& 0 \\ \hline 2^x-2 &=& 0 \\ 2^x &=& 2^1 \\ x &=& 1 \\ \mathbf{x_3} &\mathbf{=}& \mathbf{1} \\\\ 2^x+3 &=& 0 \\ 2^x &=& -3 \\ x\log(2) &=& \log(-3) \quad & |\quad \text{ no solution, $log(-3)$ complex } \\ \hline \end{array}\)

Find an ordered triple (x,y,z) of real numbers satisfying x<= y<= z and the system of equations
sqrtx + sqrty +sqrtz = 10
x+y+z=38
(sqrtxyz) = 30

\(\begin{array}{|lrcll|} \hline (1) & \sqrt{x} + \sqrt{y} +\sqrt{z} &=& 10 \\ (2) & x+y+z &=& 38 \\ (3) & \sqrt{xyz} &=& 30 \\ \hline \end{array}\)

1.

\(\begin{array}{|lrcll|} \hline & (\sqrt{x} + \sqrt{y} +\sqrt{z})^2 &=& 10^2 \\ & \underbrace{x+y+z}_{=38} +2( \sqrt{xy}+\sqrt{xz}+\sqrt{yz} ) &=& 100 \\ & 38 +2( \sqrt{xy}+\sqrt{xz}+\sqrt{yz} ) &=& 100 \quad & | \quad -38 \\ & 2( \sqrt{xy}+\sqrt{xz}+\sqrt{yz} ) &=& 62 \quad & | \quad :2 \\ \mathbf{(4)}& \mathbf{\sqrt{xy}+\sqrt{xz}+\sqrt{yz}} &\mathbf{=}& \mathbf{31} \\ \hline \end{array}\)

\(\begin{array}{lcll} \text{We substitute:} \\ \quad x_1 = \sqrt{x} & \text{ or }& x = x_1^2 \\ \quad x_2 = \sqrt{y} & \text{ or }& y = x_2^2 \\ \quad x_3 = \sqrt{z} & \text{ or }& z = x_3^2 \\ \end{array}\)

\(\begin{array}{|rcll|} \hline x_1+x_2+x_3 &=& \sqrt{x} + \sqrt{y} +\sqrt{z} \\ &=& 10 \\ x_1\cdot x_2 \cdot x_3 &=& \sqrt{xyz} \\ &=& 30 \\ x_1\cdot x_2 + x_1 \cdot x_3 + x_2 \cdot x_3 &=& \sqrt{xy}+\sqrt{xz}+\sqrt{yz} \\ &=& 31 \\ \hline \end{array}\)

\(\begin{array}{lcll} \text{We set:} \\ \quad p &=& -(x_1+x_2+x_3) \\ &=& -10 \\ \quad q &=& x_1\cdot x_2 + x_1 \cdot x_3 + x_2 \cdot x_3 \\ &=& 31 \\ \quad r &=& -(x_1\cdot x_2 \cdot x_3) \\ &=& -30 \\ \end{array}\)

\(\begin{array}{lrcll} \text{The cubic equation:} \\ \boxed{ x^3 - 10x^2+31x-30 = 0 } \\ \end{array}\)

The first solution is \(x_1 = 2\)

Long division:

\(\begin{array}{rcll} x^2-8x+15 = (x-3)(x-5) \end{array}\)

so \(x_2 = 3\) and \(x_3 = 5\)

\(\begin{array}{|rcll|} \hline x_1 = 2 & x &=& x_1^2 \\ & \mathbf{x} &\mathbf{=}& \mathbf{4} \\\\ x_2 = 3 & y &=& x_2^2 \\ & \mathbf{y} &\mathbf{=}& \mathbf{9} \\\\ x_3 = 5 & z &=& x_3^2 \\ & \mathbf{z} &\mathbf{=}& \mathbf{25} \\ \hline \end{array}\)

The ordered triple (4, 9, 25) of real numbers satisfying \(4\le 9\le 25\) and the system of equations.

Find a polynomial $f(x)$ of degree $5$ such that both of these properties hold:
$f(x)-1$ is divisible by $(x-1)^3$.
$f(x)$ is divisible by $x^3$.

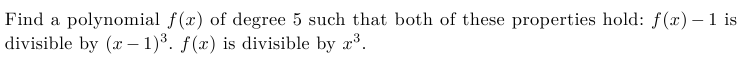
1. \(\bf{\text{ $\mathbf{f(x)}$ is divisible by $\mathbf{x^3}~$ ?}}\)

\(\begin{array}{lcll} \text{Let $f(x) = a(x-x_1)(x-x_2)(x-x_3)(x-x_4)(x-x_5)$ is a polynomial of degree $5$.} \\ \text{If f(x) is divisible by $x^3$, than $x_1=x_2=x_3=0 $} \\ \qquad f(x) = a(x-0)(x-0)(x-0)(x-x_4)(x-x_5) \\ \qquad \boxed{f(x) =ax^3(x-x_4)(x-x_5)} \text{ This polynom is divisible by $x^3$} \\ \text{expand to:} \\ \qquad f(x)= ax^5 - a(x_4+x_5)x^4 + ax_4x_5x^3 \qquad \text{Let $A=a$, $~B=a(x_4+x_5)$, and $~C = ax_4x_5 $ } \\ \text{finally we have:} \\ \qquad \boxed{f(x) = Ax^5+Bx^4+Cx^3 \qquad (1) } \text{ This polynom is divisible by $x^3$} \\ \end{array}\)

2. \(\bf{\text{ $\mathbf{f(x)-1}$ is divisible by $\mathbf{(x-1)^3}~$ ?}}\)

\(\begin{array}{lcll} \text{Say $P(x) $ is a polynom divisible by $(x-1)^3$ .} \\ \text{Set:}\\ \qquad P(x)=b\cdot(x-1)^3 \\ \qquad \text{The root is $x = 1$ }\\ \text{so}\\ \qquad P(1)=b(1-1)^3=0 \\ \text{Set also:}\\ \qquad \text{ $P'(x)= 3b(x-1)^2 $}\\ \text{so}\\ \qquad P'(1)= 3b(1-1)^2=0 \\ \text{Set finally:}\\ \qquad \text{ $P''(x)= 6b(x-1) $}\\ \text{so}\\ \qquad P''(1)= 6b(1-1)^2=0 \\\\ \text{Conclusion} \\ \text{If $P(x)$ is divisible by $(x-1)^3$, so $\boxed{\mathbf{P(1)=P'(1)=P''(1)=0}\qquad (2)}$ at the root $x=1$ } \\ \end{array}\)

\(\begin{array}{lrcll} \text{We set:}\\ \text{1)}& f(x) - 1 &=& P(x) \quad & | \quad \text{$f(x)-1$ and $P(x)$ are divisible by $(x-1)^3 $ }\\ & f(1) -1 &=& P(1) = 0 \quad & | \quad \rightarrow (2) \\\\ \text{2)}& (f(x) - 1)' &=& P'(x) \\ & f'(x) &=& P'(x) \\ & f'(1) &=& P'(1) = 0 \quad & | \quad \rightarrow (2) \\\\ \text{3)}& (f(x) - 1)'' &=& P''(x) \\ & f''(x) &=& P''(x) \\ & f''(1) &=& P''(1) = 0 \quad & | \quad \rightarrow (2) \\ \end{array}\)

\(\begin{array}{lrcll} \text{We see:}\\ & \boxed{ \begin{array}{r} f(1) -1 = 0 \qquad (3) \\ f'(1) = 0 \qquad (4) \\ f''(1)= 0 \qquad (5) \\ \end{array} } \end{array}\)

\(\begin{array}{lrcll} \text{We calculate:}\\ & f(x) &=& Ax^5+Bx^4+Cx^3 \\ & f(x) -1 &=& Ax^5+Bx^4+Cx^3 - 1 \\ & f(1)-1 &=& A+B+C -1 = 0 \quad & | \quad \rightarrow (3) \\\\ & f'(x) &=& 5Ax^4+4Bx^3+3Cx^2 \\ & f'(1) &=& 5A+4B+3C = 0 \quad & | \quad \rightarrow (4) \\\\ & f''(x) &=& 20Ax^3+12Bx^2+6Cx \\ & f''(1) &=& 20A+12B+6C = 0 \quad & | \quad \rightarrow (5) \\ \end{array}\)

\(\begin{array}{lrcll} \text{Solve the Simultaneous Equations, we calculate $A~$, $B~$, $C~$ :} \\ \end{array}\\ \begin{array}{lrcll} A+B+C -1 = 0 \quad \Rightarrow & A+B+C &=& 1 \\ & 5A+4B+3C &=& 0 \\ & 20A+12B+6C &=& 0 \\ \end{array}\)

Cramer's Rule:

\(\begin{array}{rcrcrcr} 1\cdot A &+& 1\cdot B &+& 1\cdot C &=& 1 \\ 5\cdot A &+& 4\cdot B &+& 3\cdot C &=& 0 \\ 20\cdot A &+& 12\cdot B &+& 6\cdot C &=& 0 \\ \end{array}\\ \small{ \begin{array}{lcl} \\ \text{Determinant denominator} &=& \begin{vmatrix} 1&1&1 \\ 5&4&3 \\ 20&12&6 \\ \end{vmatrix}\\ \\ &=& 1\cdot 4\cdot 6 + 5\cdot 12\cdot 1 +20\cdot 1\cdot 3 - 20\cdot 4\cdot 1 -1\cdot 12\cdot 3 -5\cdot 1\cdot 6\\ &=& 24+60+60-80-36-30 \\ &=& -2 \\ \end{array} } \)

\(\begin{array}{lcl} A &=& \dfrac{ \begin{vmatrix} 1&1&1 \\ 0&4&3 \\ 0&12&6 \\ \end{vmatrix} }{-2}\\\\ &=&\dfrac{ 1\cdot 4\cdot 6 - 1\cdot 12\cdot 3 } {-2}\\ &=&\dfrac{ -12 } {-2}\\\\ \mathbf{A} & \mathbf{=} & \mathbf{6}\\ \end{array} \begin{array}{lcl} B &=& \dfrac{ \begin{vmatrix} 1&1&1 \\ 5&0&3 \\ 20&0&6 \\ \end{vmatrix} }{-2}\\\\ &=&\dfrac{ 20\cdot 1\cdot 3 - 5\cdot 1\cdot 6 } {-2}\\ &=&\dfrac{ 30 } {-2}\\\\ \mathbf{B} & \mathbf{=} & \mathbf{-15}\\ \end{array} \begin{array}{lcl} C &=& \dfrac{ \begin{vmatrix} 1&1&1 \\ 5&4&0 \\ 20&12&0 \\ \end{vmatrix} }{-2}\\\\ &=&\dfrac{ 5\cdot 12\cdot 1 - 20\cdot 4\cdot 1 } {-2}\\ &=&\dfrac{ -20 } {-2}\\\\ \mathbf{C} & \mathbf{=} & \mathbf{10}\\ \end{array}\)

\(\begin{array}{lrcll} \text{The Polynom $f(x) = Ax^5+Bx^4+Cx^3$ with $A=6$, $~B=-15$, and $~C = 10$}\\ \quad \boxed{f(x)=6x^5-15x^4+10x^3} \end{array}\)

Proof:

\(\begin{array}{|rcll|} \hline f(3) &=& 6\cdot 3^5-15\cdot 3^4 + 10 \cdot 3^3 \\ &=& 1458-1215+270 \\ &=& 513 \\ \frac{f(3)}{3^3} &=& \frac{513}{3^3} \\ &=& 19\ \checkmark \\ \frac{f(3)-1}{(3-1)^3} &=& \frac{513-1}{2^3} \\ &=& \frac{512}{8} \\ &=& 64\ \checkmark \\ \hline \end{array}\)

Consider all the points in the plane that solve the equation x^2 + 2y^2 = 16.
Find the maximum value of the product xy on this graph.  
(This graph is an example of an "ellipse".)

Formula: Ellipse equation
\(\begin{array}{|rcll|} \hline \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2} &=& 1 \\ (xy)_{\text{max}} &=& \dfrac{ab}{2}\\ \hline \end{array}\)

Proof:

\(\begin{array}{|rcll|} \hline \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2} &=& 1 \quad & | \quad \cdot x^2 \\\\ \dfrac{x^4}{a^2}+\dfrac{x^2y^2}{b^2} &=& x^2 \quad & | \quad \mathbf{z=xy} \\\\ \dfrac{x^4}{a^2}+\dfrac{\mathbf{z}^2}{b^2} &=& x^2 \\\\ \dfrac{x^4}{a^2}+\dfrac{\mathbf{z}^2}{b^2} &=& x^2 \quad & | \quad -\dfrac{x^4}{a^2} \\\\ \dfrac{\mathbf{z}^2}{b^2} &=& x^2 -\dfrac{x^4}{a^2} \quad & | \ \text{Differentiate each term with respect to x}\\\\ \dfrac{\mathbf{2z\ dz}}{b^2} &=& 2x\ dx -\dfrac{4x^3\ dx}{a^2} \quad & | \quad :2 \\\\ \dfrac{\mathbf{ z\ dz}}{b^2} &=& x\ dx -\dfrac{2x^3\ dx}{a^2} \quad & | \quad :\ dx \\\\ \dfrac{\mathbf{ z}}{b^2}\cdot\frac{\mathbf{dz}}{dx}\ &=& x-\dfrac{2x^3}{a^2} \quad & | \quad \text{set } \frac{ \mathbf{dz}}{dx} = 0 \Rightarrow \mathbf{ z}_{\text{max}} =(xy)_{\text{max}} \\\\ x-\dfrac{2x^3}{a^2} &=& 0 \\\\ x-\dfrac{2x^3}{a^2} &=& 0 \\\\ x\left(1- \dfrac{2x^2}{a^2} \right) &=& 0 \\ \hline \end{array}\)

1. \(x = 0\) no solution \(\Rightarrow xy = 0 \) no maximum

2. x = ?

\(\begin{array}{rcll} 1- \dfrac{2x^2}{a^2} &=& 0 \\\\ \dfrac{2x^2}{a^2} &=& 1 \\\\ x^2 &=& \dfrac{a^2}{2} \quad & | \quad \pm\sqrt{} \\\\ x &=& \pm \dfrac{a}{\sqrt{2}} \quad & | \quad \cdot \frac{\sqrt{2}}{\sqrt{2}} \\\\ \mathbf{ x } &\mathbf{=}& \mathbf{ \pm a\cdot \dfrac{\sqrt{2}}{2} } \end{array} \)

y = ?

\(\begin{array}{rcll} \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2} &=& 1 \quad & | \quad \mathbf{ x } &\mathbf{=}& \mathbf{ \pm \dfrac{a}{\sqrt{2}} } \\\\ \dfrac{a^2}{2a^2}+\dfrac{y^2}{b^2} &=& 1 \\\\ \dfrac{1}{2}+\dfrac{y^2}{b^2} &=& 1 \quad & | \quad -\dfrac12 \\\\ \dfrac{y^2}{b^2} &=& 1 -\dfrac12 \\\\ \dfrac{y^2}{b^2} &=& \dfrac12 \\\\ y^2 &=& \dfrac{b^2}{2} \quad & | \quad \pm\sqrt{} \\\\ y &=& \pm \dfrac{b}{\sqrt{2}} \quad & | \quad \cdot \frac{\sqrt{2}}{\sqrt{2}} \\\\ \mathbf{ y } &\mathbf{=}& \mathbf{ \pm b\cdot \dfrac{\sqrt{2}}{2} } \end{array}\)

xy = ?

\(\begin{array}{|rcll|} \hline \mathbf{ z}_{\text{max}} =(xy)_{\text{max}} \\ (xy)_{\text{max}} &=& \mathbf{ \left(\pm a\cdot \dfrac{\sqrt{2}}{2} \right) } \cdot \mathbf{ \left( \pm b\cdot \dfrac{\sqrt{2}}{2} \right) } \quad & | \quad xy > 0! \\\\ &=& a\cdot \dfrac{\sqrt{2}}{2}\cdot b\cdot \dfrac{\sqrt{2}}{2} \\\\ &=& ab\cdot \dfrac{\sqrt{2}}{2} \cdot \dfrac{\sqrt{2}}{2} \\\\ \mathbf{(xy)_{\text{max}}} &\mathbf{=}& \mathbf{ \dfrac{ab}{2} } \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline x^2 + 2y^2 &=& 16 \quad & | \quad : 16 \\\\ \dfrac{x^2}{16} + \dfrac{2y^2}{16} &=& 1 \\\\ \dfrac{x^2}{16} + \dfrac{ y^2}{8} &=& 1 \\\\ \dfrac{x^2}{\mathbf{4}^2} + \dfrac{ y^2}{(\mathbf{\sqrt{8}})^2} &=& 1 \\\\ \text{so } a = 4 \text{ and } b = \sqrt{8} \\\\ \mathbf{(xy)_{\text{max}}} &\mathbf{=}& \mathbf{ \dfrac{ab}{2} } \\\\ &=& \dfrac{4 \sqrt{8}}{2} \\\\ &=& 2 \sqrt{8} \\ &=& 2 \sqrt{2\cdot4 } \\ &=& 2\cdot2 \sqrt{2} \\ \mathbf{(xy)_{\text{max}}} &\mathbf{=}& \mathbf{4 \sqrt{2}} \\ \hline \end{array} \)

\(\begin{array}{rcll} Point_1 &=& ( a\cdot \dfrac{\sqrt{2}}{2},~ b\cdot \dfrac{\sqrt{2}}{2} ) \\ &=& ( 4\cdot \dfrac{\sqrt{2}}{2},~ \sqrt{8}\cdot \dfrac{\sqrt{2}}{2} ) \\ &=& ( 2\cdot \sqrt{2} ,~ \dfrac{\sqrt{16}}{2} ) \\ &=& ( 2\cdot \sqrt{2} ,~ \dfrac{4}{2} ) \\ &=& ( 2\cdot \sqrt{2} ,~ 2 ) \\ \end{array} \begin{array}{rcll} Point_2 &=& ( -a\cdot \dfrac{\sqrt{2}}{2},~ -b\cdot \dfrac{\sqrt{2}}{2} ) \\ &=& ( -4\cdot \dfrac{\sqrt{2}}{2}, -\sqrt{8}\cdot \dfrac{\sqrt{2}}{2} ) \\ &=& ( -2\cdot \sqrt{2} ,~ -\dfrac{\sqrt{16}}{2} ) \\ &=& ( -2\cdot \sqrt{2} ,~ -\dfrac{4}{2} ) \\ &=& ( -2\cdot \sqrt{2} ,~ -2 ) \\ \end{array} \)

A palindrome is a positive integer which reads the same forward and backwards, like  12321 or 8448.
How many 4-digit palindromes are divisible by 3?

\(\begin{array}{|r|r|r|r|} \hline & n & \text{palindrome } a(n) & \text{divisible by } 3 \\ \hline & 110& 10\ 01 \\ & 111& 11\ 11 \\ 1. & 112& 12\ 21 & \checkmark \\ & 113& 13\ 31 \\ & 114& 14\ 41 \\ 2. & 115& 15\ 51 &\checkmark \\ & 116& 16\ 61 \\ & 117& 17\ 71 \\ 3. & 118& 18\ 81 &\checkmark \\ & 119& 19\ 91 \\ \hline & 120& 20\ 02 \\ 4. & 121& 21\ 12 &\checkmark \\ & 122& 22\ 22 \\ & 123& 23\ 32 \\ 5. & 124& 24\ 42 &\checkmark \\ & 125& 25\ 52 \\ & 126& 26\ 62 \\ 6. & 127& 27\ 72 &\checkmark \\ & 128& 28\ 82 \\ & 129& 29\ 92 \\ \hline 7. & 130& 30\ 03 &\checkmark \\ & 131& 31\ 13 \\ & 132& 32\ 23 \\ 8. & 133& 33\ 33 &\checkmark \\ & 134& 34\ 43 \\ & 135& 35\ 53 \\ 9. & 136& 36\ 63 &\checkmark \\ & 137 & 37\ 73 \\ & 138& 38\ 83 \\ 10. & 139& 39\ 93 &\checkmark \\ \hline & 140& 40\ 04 \\ & 141& 41\ 14 \\ 11. & 142& 42\ 24 &\checkmark \\ & 143& 43\ 34 \\ & 144& 44\ 44 \\ 12. & 145& 45\ 54 &\checkmark \\ & 146& 46\ 64 \\ & 147& 47\ 74 \\ 13. & 148& 48\ 84 &\checkmark \\ & 149& 49\ 94 \\ \hline & 150& 50\ 05 \\ 14. & 151& 51\ 15 &\checkmark \\ & 152& 52\ 25 \\ & 153& 53\ 35 \\ 15. & 154& 54\ 45 &\checkmark \\ & 155& 55\ 55 \\ & 156& 56\ 65 \\ 16. & 157& 57\ 75 &\checkmark \\ & 158& 58\ 85 \\ & 159& 59\ 95 \\ \hline 17. & 160& 60\ 06 &\checkmark \\ & 161& 61\ 16 \\ & 162& 62\ 26 \\ 18. & 163& 63\ 36 &\checkmark \\ & 164& 64\ 46 \\ & 165& 65\ 56 \\ 19. & 166& 66\ 66 &\checkmark \\ & 167& 67\ 76 \\ & 168& 68\ 86 \\ 20. & 169& 69\ 96 &\checkmark \\ \hline & 170& 70\ 07 \\ & 171& 71\ 17 \\ 21. & 172& 72\ 27 &\checkmark \\ & 173& 73\ 37 \\ & 174& 74\ 47 \\ 22. & 175& 75\ 57 &\checkmark \\ & 176& 76\ 67 \\ & 177& 77\ 77 \\ 23. & 178& 78\ 87 &\checkmark \\ & 179& 79\ 97 \\ \hline & 180& 80\ 08 \\ 24. & 181& 81\ 18 &\checkmark \\ & 182& 82\ 28 \\ & 183& 83\ 38 \\ 25. & 184& 84\ 48 &\checkmark \\ & 185& 85\ 58 \\ & 186& 86\ 68 \\ 26. & 187& 87\ 78 &\checkmark \\ & 188& 88\ 88 \\ & 189& 89\ 98 \\ \hline 27. & 190& 90\ 09 &\checkmark \\ & 191& 91\ 19 \\ & 192& 92\ 29 \\ 28. & 193& 93\ 39 &\checkmark \\ & 194& 94\ 49 \\ & 195& 95\ 59 \\ 29. & 196& 96\ 69 &\checkmark \\ & 197& 97\ 79 \\ & 198& 98\ 89 \\ 30. & 199& 99\ 99 &\checkmark \\ \hline \end{array}\)

30  4-digit palindromes are divisible by 3.

find parametric equation for rectangular equation:

y = x^2 - 4x + 7

\(\begin{array}{|lcll|} \hline \text{ $y = x^2 - 4x + 7$ is a rectangular equation. }\\ \text{Find a set of parametric equations for the equation } y = x^2 - 4x + 7 \\\\ \text{Solution }: \\ \text{Assign any one of the variable equal to $t$ . (say $x = t$ ). } \\ \text{Then, the given equation can be rewritten as $y=t^2 - 4t +7$ .}\\ \text{Therefore, a set of parametric equations is $x = t$ and $y=t^2 - 4t +7$. }\\ \hline \end{array} \)