Tan Theta = -8/15, Pi/2<Theta<pi
sorry, i dont know how to put the symbols for Pi and Theta in :P
Tan Theta = -8/15, Pi/2<Theta<pi
First this is the second quad so
sin and cosec are positive and the rest will be negative.
Now you don't need to worry about again until the end.

Finsd the length of the hypotenuse using pythagoras's theorum
then read the ratios straight of the triangle and assign the appropriate signs. ![]()
Since we have a second quadrant angle, we have that a = 8 and b = -15 so h = √[(-8)^2 + (15)^2 ] = √(64 + 225) = √289) = 17
Here is a review of the 6 basic trig functions.....it should help....
The sine of an angle is the ratio of the length of the opposite side to the length of the hypotenuse. (The word comes from the Latin sinus for gulf or bay,[1] since, given a unit circle, it is the side of the triangle on which the angle opens.) In our case
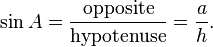
This ratio does not depend on the size of the particular right triangle chosen, as long as it contains the angle A, since all such triangles are similar.
The cosine of an angle is the ratio of the length of the adjacent side to the length of the hypotenuse: so called because it is the sine of the complementary or co-angle.[2] In our case
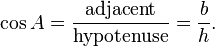
The tangent of an angle is the ratio of the length of the opposite side to the length of the adjacent side: so called because it can be represented as a line segment tangent to the circle, that is the line that touches the circle, from Latin linea tangens or touching line (cf. tangere, to touch).[3] In our case
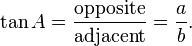
The acronyms "SOHCAHTOA" ("Soak-a-toe", "Sock-a-toa", "So-kah-toa") and "OHSAHCOAT" are commonly used mnemonics for these ratios.
The remaining three functions are best defined using the above three functions.
The cosecant csc(A), or cosec(A), is the reciprocal of sin(A); i.e. the ratio of the length of the hypotenuse to the length of the opposite side:
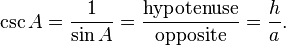
The secant sec(A) is the reciprocal of cos(A); i.e. the ratio of the length of the hypotenuse to the length of the adjacent side:
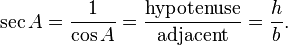
It is so called because it represents the line that cuts the circle (from Latin: secare, to cut).[4]
The cotangent cot(A) is the reciprocal of tan(A); i.e. the ratio of the length of the adjacent side to the length of the opposite side:
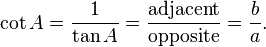
![]()
![]()
![]()
Tan Theta = -8/15, Pi/2<Theta<pi
First this is the second quad so
sin and cosec are positive and the rest will be negative.
Now you don't need to worry about again until the end.

Finsd the length of the hypotenuse using pythagoras's theorum
then read the ratios straight of the triangle and assign the appropriate signs. ![]()