Let F(x) be the real-valued function defined for all real x except for x = 0 and x = 1 and satisfying the functional equation \(F(x) + F\left(\frac{x-1}x\right) = 1+x\).Find the F(x) satisfying these conditions. Write F(x) as a rational function with expanded polynomials in the numerator and denominator.
Let F(x) be the real-valued function defined for all real x except for x = 0 and x = 1 and satisfying
the functional equation
\(F(x) + F\left(\frac{x-1}x\right) = 1+x.\)
F(x) + F\left(\frac{x-1}x\right) = 1+x.
Find the F(x) satisfying these conditions.
Write F(x) as a rational function with expanded polynomials in the numerator and denominator.
\(\begin{array}{|lrclcl|} \hline & F(x) + F\left(\frac{x-1}x\right) &=& 1+x \qquad (1) \\\\ \text{Set in (1) }x=\frac{x-1}{x}: & F\left(\frac{x-1}x\right) + F\left(\frac1{1-x}\right) &=& 1+\frac{x-1}{x} \qquad (2) \\\\ \text{Set in (1) }x=\frac1{1-x}: & F\left(\frac1{1-x}\right) + F(x) &=& 1+\frac1{1-x} \qquad (3) \\\\ \hline \\ (1) - (2) + (3): & F(x) + F\left(\frac{x-1}x\right) \\ & - \Big(F\left(\frac{x-1}x\right) + F\left(\frac1{1-x}\right) \Big) \\ & + F\left(\frac1{1-x}\right) + F(x) &=& 1+x -(1+\frac{x-1}{x}) + 1+\frac1{1-x} \\\\ & F(x) + F\left(\frac{x-1}x\right) \\ & -F\left(\frac{x-1}x\right) - F\left(\frac1{1-x}\right) \\ & + F\left(\frac1{1-x}\right) + F(x) &=& 1+x -(1+\frac{x-1}{x}) + 1+\frac1{1-x} \\\\ & 2F(x) &=& 1+x -(1+\frac{x-1}{x}) + 1+\frac1{1-x} \\ & 2F(x) &=& 1+x -1-\frac{x-1}{x} + 1+\frac1{1-x} \\ & 2F(x) &=& 1+x -\frac{x-1}{x} +\frac1{1-x} \\ & 2F(x) &=& 1+x +\frac{1-x}{x} +\frac1{1-x} \\\\ & 2F(x) &=& \dfrac{(1+x)x(1-x)+(1-x)^2+x}{x(1-x)} \\\\ & 2F(x) &=& \dfrac{(1-x^2)x+1-2x+x^2+x}{x(1-x)} \\\\ & 2F(x) &=& \dfrac{(1-x^2)x+1-x+x^2}{x(1-x)} \\\\ & 2F(x) &=& \dfrac{ x-x^3 +1-x+x^2}{x(1-x)} \\\\ & 2F(x) &=& \dfrac{ 1+x^2-x^3}{x(1-x)} \\\\ & F(x) &=& \dfrac{ 1+x^2-x^3}{2x(1-x)} \\\\ & \mathbf{F(x)} & \mathbf{=} & \mathbf{\dfrac{ 1+x^2-x^3}{2x - 2x^2}} \\ \hline \end{array}\)
graph:
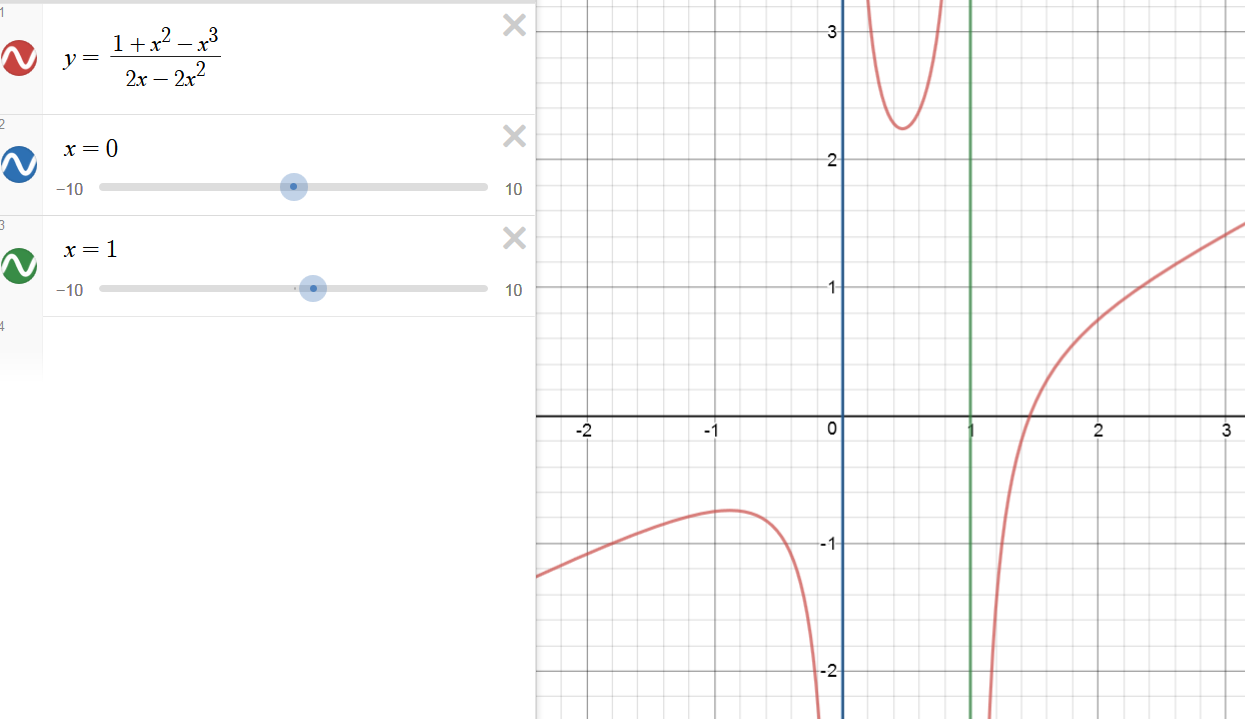
![]()