Hi! :) is there a way to get the answer in radical form of $$\underset{\,\,\,\,^{\textcolor[rgb]{0.66,0.66,0.66}{360^\circ}}}{{sin}}{\left({\frac{{\frac{{\mathtt{3}}{\mathtt{\,\times\,}}{\mathtt{\pi}}}{{\mathtt{2}}}}}{{\mathtt{2}}}}\right)} = {\mathtt{0.041\: \!111\: \!761\: \!829}}$$ can anyone help me?
sin(3pi/2/2) ?
$$\sin_{(rad)} \left(\dfrac{ \dfrac{3\cdot \pi}{2} }{2} \right)
=\sin_{(rad)} \left( \dfrac{3\cdot \pi}{4} \right)=\frac{1}{2}\sqrt{2}\\\\
\dfrac{3\cdot \pi}{4}\; \rm{rad} \equiv 135 \ensurement{^{\circ}}\\\\
\sin_{(360 \ensurement{^{\circ}} )} \left(135 \ensurement{^{\circ}} \right)
= \frac{1}{2}\sqrt{2}\\\\$$
 (°) (°) |  (rad) (rad) | 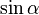 |  | 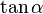 |  |
|---|---|---|---|---|---|
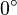 |  |  |  |  | 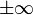 |
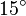 |  | 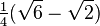 | 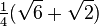 | 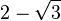 |  |
 |  |  | 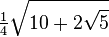 | 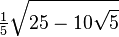 |  |
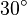 | 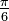 |  |  | 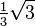 | 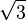 |
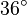 | 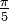 |  |  | 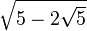 | 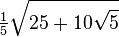 |
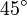 |  |  |  | 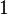 |  |
 |  |  |  |  |  |
 |  |  |  | 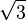 | 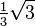 |
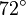 | 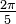 | 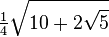 |  |  | 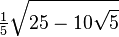 |
 | 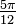 | 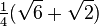 | 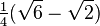 |  | 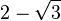 |
 |  |  |  | 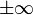 |  |
 | 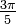 |  |  |  |  |
 | 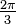 |  | 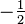 |  | 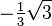 |
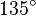 | 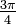 |  | 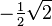 | 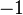 | 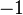 |
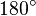 | 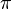 |  | 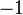 |  | 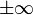 |
 |  | 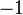 |  | 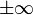 |  |
 | 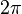 |  |  |  |
|
sin(3pi/2/2) ?
$$\sin_{(rad)} \left(\dfrac{ \dfrac{3\cdot \pi}{2} }{2} \right)
=\sin_{(rad)} \left( \dfrac{3\cdot \pi}{4} \right)=\frac{1}{2}\sqrt{2}\\\\
\dfrac{3\cdot \pi}{4}\; \rm{rad} \equiv 135 \ensurement{^{\circ}}\\\\
\sin_{(360 \ensurement{^{\circ}} )} \left(135 \ensurement{^{\circ}} \right)
= \frac{1}{2}\sqrt{2}\\\\$$
 (°) (°) |  (rad) (rad) | 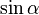 |  | 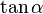 |  |
|---|---|---|---|---|---|
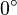 |  |  |  |  | 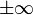 |
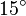 |  | 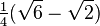 | 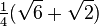 | 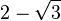 |  |
 |  |  | 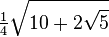 | 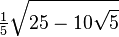 |  |
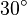 | 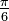 |  |  | 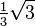 | 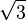 |
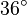 | 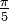 |  |  | 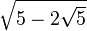 |  |
 |  |  |  |  |  |
 |  |  |  | 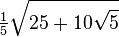 | 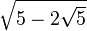 |
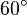 |  |  |  | 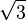 |  |
 |  |  |  |  |  |
 |  |  |  |  | 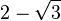 |
 |  |  |  | 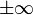 |  |
 | 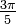 | 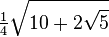 | 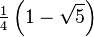 | 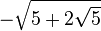 |  |
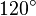 | 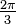 |  | 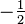 |  | 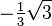 |
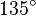 | 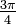 |  | 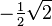 | 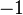 | 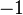 |
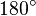 | 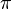 |  | 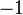 |  | 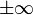 |
 |  | 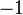 |  | 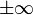 |  |
 | 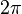 |  |  |  |
|