If we know the degree measure, we can use the following "formula"....
[degree measure / 360] x [2*pi*r] = s (where s = arc length)
If you have taken Trig, you might be familiar with "radian" measure ("rads")
The "formula" for this is
s = rΘ (where Θ is in "rads")
![]()
![]()
![]()
SlicesThere are two main "slices" of a circle:
| 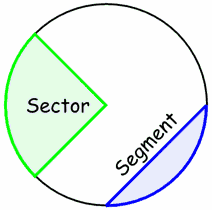 |
| Sector | Segment |
|---|---|
The Quadrant and Semicircle are two special types of Sector:
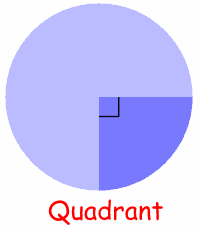 | Quarter of a circle is called a Quadrant. Half a circle is called a Semicircle. |
 |
Area of a SectorYou can work out the Area of a Sector by comparing its angle to the angle of a full circle. Note: I am using radians for the angles. | 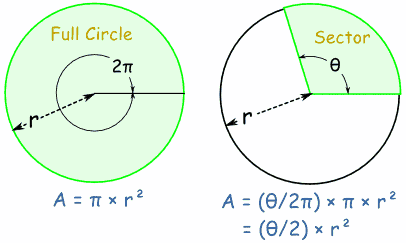 |
This is the reasoning:
Area of Sector = ½ × θ × r2 (when θ is in radians) Area of Sector = ½ × (θ × π/180) × r2 (when θ is in degrees) | |
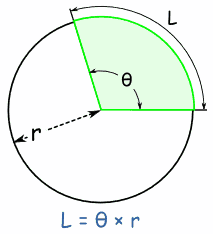 | Arc LengthBy the same reasoning, the arc length (of a Sector or Segment) is: L = θ × r (when θ is in radians) L = (θ × π/180) × r (when θ is in degrees) |
Area of SegmentThe Area of a Segment is the area of a sector minus the triangular piece (shown in light blue here). There is a lengthy reason, but the result is a slight modification of the Sector formula: | 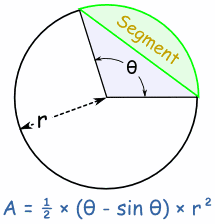 |
Area of Segment = ½ × (θ - sin θ) × r2 (when θ is in radians) Area of Segment = ½ × ( (θ × π/180) - sin θ) × r2 (when θ is in degrees) | |
Great pictures here. Thanks anonymous.
I am confused by the question. A segment has an area and it has a circumference but it does not have a length. So what is it that you really wanted?
Ninja, I love all these circle definitions. do you think that they should make there way into one of your threads? I'm not sure which one. Umm I guess if you reference the info post directly it can go straight inot the reference post. What do you think?
If you click on the title of the post that you want (rather than the thread) then you will reference directly to THAT post.
Thanks