+130458 Archimedes provided a rather ingenious proof of this by noting that the volume of a hemisphere is equal to the sum of the differences in the cross-sections of a cylinder and an associated cone both having the same radius as the hemisphere, i.e....... pi*r^2h - (1/3)pi*r^2h = (2/3)pi*r^2h. But, the cylinder and the cone also have a height equal to this radius, so we have (2/3)pi*r^2h = (2/3)pi*r^2*r = (2/3)pi*r^3
So....twice this equals the volume of a whole sphere = 4/3pi*r^3
+270 Volume of the sphere = 4/3ㅠr^3
Where, r = radius of the sphere
Derivation for Volume of the Sphere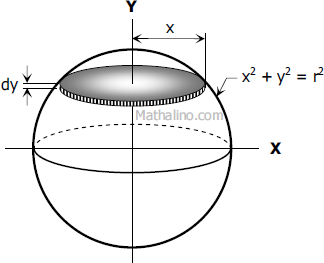
The differential element shown in the figure is cylindrical with radius x and altitude dy. The volume of cylindrical element is...
The sum of the cylindrical elements from 0 to r is a hemisphere, twice the hemisphere will give the volume of the sphere. Thus,
From the equation of the circle x2 + y2 = r2; x2 = r2 - y2.
![$ V = 2\pi \left[ r^2y - \dfrac{y^3}{3} \right]_0^r $](/api/ssl-img-proxy?src=http%3A%2F%2Fwww.mathalino.com%2Ffiles%2Ftex%2F6f174b9ec95e195e940d347c8f5cbc0509cde847.png)
![$ V = 2\pi \left[ \left(r^3 - \dfrac{r^3}{3}\right) - \left(0 - \dfrac{0^3}{3}\right) \right] $](/api/ssl-img-proxy?src=http%3A%2F%2Fwww.mathalino.com%2Ffiles%2Ftex%2Fcdc01e36e00d16c2285c8349049f778546fb4859.png)
![$ V = 2\pi \left[ \dfrac{2r^3}{3} \right] $](/api/ssl-img-proxy?src=http%3A%2F%2Fwww.mathalino.com%2Ffiles%2Ftex%2F54dfb5bb7bf43d9a3afe051b24bf571d6959dc1e.png)
+130458 Archimedes provided a rather ingenious proof of this by noting that the volume of a hemisphere is equal to the sum of the differences in the cross-sections of a cylinder and an associated cone both having the same radius as the hemisphere, i.e....... pi*r^2h - (1/3)pi*r^2h = (2/3)pi*r^2h. But, the cylinder and the cone also have a height equal to this radius, so we have (2/3)pi*r^2h = (2/3)pi*r^2*r = (2/3)pi*r^3
So....twice this equals the volume of a whole sphere = 4/3pi*r^3
+118696 Welcome to the forum fiflvm97. I hope that ou like it here. 
I can see that you will be a great asset to us if you choose to stay around :)
---------------------------------------------------------------------
I have been looking at these answers.
Geno, yours is concise but exactly what the asker would have wanted. 
flflvm, I loved your analysis of this answer. Adding the diagram made all the difference too.
I hope that some of our senior students really think about what you said - as I did. It would be of great benefit to them.
Chris, I had not thought before about the volume of a cone being one third of a hemisphere. It's an obvious conclusion now that you point it out.
As for the rest of what archimedes said that will require a more concentrated effort from me. Thank you for discussing it.
+130458 Melody......there used to be a very good illustration of this on the net, but I'm unable to find it, now. However, this one is pretty good......http://mathcentral.uregina.ca/QQ/database/QQ.09.01/rahul1.html
