
Based on one of the properties of a centroid. Segment GD is 1/3 the length of AD.
Sorry my method is pretty complicated so hang on.
Triangles ABD and ABC are similar. Since D is the midpoint, and they share AB as a side, their ratio is 1:2
We can find the area of ABC using Heron's formula. After one million years, we have a simplified radical of \(2\sqrt{4466}\).
Since their ratio is 1:2, we know that the area of ABD is now \(\sqrt{4466}\).
Side BD is 18 / 2 = 9
We know sides AB = 15 and BD = 9. So we can work backwards from Heron's formula to find the length of AD.
Working backwards from heron's formula: 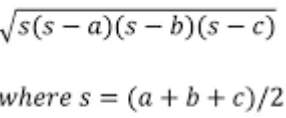
we calculate s. Since the length of side C is unknown, we can call it X.
We find that S is 12 + 0.5x. We know the area is \(\sqrt{4466}\). So we can make the following equation:
\((0.5x+12)(0.5x+12-15)(0.5x+12-9)(0.5x+12-x)=4466\)
(0.5x+12)(0.5x-3)*(0.5x+3)(0.5x+12-x)=4466 = {x=-(2*sqrt(86)), x=2*sqrt(86), x=-(2*sqrt(67)), x=2*sqrt(67)}
So side C is either \(2\sqrt{86}\), or \(2\sqrt{67}\).
That means GD is either: \(\frac{2\sqrt{86}}{3}\), or \(\frac{2\sqrt{67}}{3}\)....
Yup! THis is completely messed up! What a crazy method! I got two possible sides too, uh.. Help?