heureka

What is the derivative of this function?

\(g(t) = (t^3+3t^2+t)/(t^3)\)

g(t) = (t^3+3t^2+t)/(t^3)

I'm not getting how the extended power rule works

Formula power rule:

\(\begin{array}{|rcll|} \hline f(x) &=& x^n,\quad n \ne 0 \\ f'(x) &=& n\cdot x^{n-1} \\ \hline \end{array} \)

\(\begin{array}{|rcll|} \hline g(t) &=& \dfrac{t^3+3t^2+t} {t^3} \\\\ &=& \dfrac{t^3} {t^3} +\dfrac{3t^2} {t^3}+\dfrac{t} {t^3} \\\\ &=& 1 + 3\cdot t^{2-3} + t^{1-3} \\\\ &=& 1 + 3\cdot t^{-1} + t^{-2} \quad & | \quad \text{power rule} \\\\ g'(x) &=& 0 + 3\cdot \left((-1)\cdot t^{-1-1} \right)+ (-2) \cdot t^{-2-1} \\\\ &=& -3\cdot t^{-2} - 2 \cdot t^{-3} \\\\ &=& - \dfrac{3}{t^2} - \dfrac{2}{t^3} \\\\ \hline \end{array} \)

Logarithm Question

Evaluate

\(\huge{ \log_{\sqrt[3]{5}}125 } \)

\huge{ \log_{\sqrt[3]{5}}125 }

Formula:

\(\begin{array}{|rcll|} \hline \log_b(x) &=& \dfrac{\log_c(x)}{\log_c(b)} \\ \hline \end{array} \)

\(\begin{array}{|rcll|} \hline && \log_{\sqrt[3]{5}}125 \\\\ &=& \dfrac{ \ln(125) } { \ln(\sqrt[3]{5}) } \\\\ &=& \dfrac{ \ln(5^3) } { \ln(5^{\frac13}) } \\\\ &=& \dfrac{ 3\cdot \ln(5) } {\frac13\cdot \ln(5) } \\\\ &=& \dfrac{ 3 } {\frac13 } \\\\ &=& 3\cdot \frac31 \\\\ &=& 9 \\ \hline \end{array}\)

Beweisen Sie mit Hilfe der vollständigen Induktion folgende Aussage für alle natürlichen Zahlen n:
\huge{\sum \limits_{i=1}^{n} \frac{i}{2^i}=2-\frac{n+2}{2^n}}

\(\huge{\sum \limits_{i=1}^{n} \frac{i}{2^i}=2-\frac{n+2}{2^n}} \)

Induktionsanfang:

n = 1:    linke Seite: \(\dfrac{1}{2^1 } = \dfrac{1}{2}\)
          rechte Seite:  \(2-\dfrac{1+2}{2^1} = 2-\dfrac{3}{2} = \dfrac{1}{2}\)
Für n=1 sind beide Seiten gleich!

Die Induktionsannahme (I.A.) lautet:
\( \displaystyle \sum \limits_{i=1}^{n} \frac{i}{2^i}=2-\frac{n+2}{2^n}\)

Induktionsbehauptung:

\(\displaystyle \sum \limits_{i=1}^{n+1} \frac{i}{2^i}=2-\frac{(n+1)+2}{2^{n+1}}\)

Beweis des Induktionsschritts \(n\rightarrow n+1:\)

\(\begin{array}{|lrcll|} \hline n+1:\\ \text{linke Seite:} \\ && & \displaystyle \sum \limits_{i=1}^{n+1} \frac{i}{2^i} \\\\ &&=& \displaystyle \sum \limits_{i=1}^{n} \frac{i}{2^i} + \dfrac{n+1}{2^{n+1}} \\\\ &&\overset{I.A.}{=}& \displaystyle 2-\frac{n+2}{2^n} + \dfrac{n+1}{2^{n+1}} \\\\ &&=& \displaystyle 2- \left( \frac{n+2}{2^n} - \dfrac{n+1}{2^{n+1}} \right) \\\\ &&=& \displaystyle 2- \left[ \frac{n+2}{2^n}\cdot\left(\dfrac{2}{2}\right) - \dfrac{n+1}{2^{n+1}} \right] \\\\ &&=& \displaystyle 2- \left( \frac{(n+2)\cdot 2}{2^n\cdot 2} - \dfrac{n+1}{2^{n+1}} \right) \\\\ &&=& \displaystyle 2- \left( \frac{(n+2)\cdot 2}{2^{n+1}} - \dfrac{n+1}{2^{n+1}} \right) \\\\ &&=& \displaystyle 2- \frac{(n+2)\cdot 2-(n+1)}{2^{n+1}} \\\\ &&=& \displaystyle 2- \frac{2n+4-n-1} {2^{n+1}} \\\\ &&=& \displaystyle 2- \frac{n+3}{2^{n+1}} \\\\ &&=& \displaystyle 2- \frac{(n+1)+2}{2^{n+1}} \\\\ \text{rechte Seite:} \\ &&& \displaystyle 2-\frac{(n+1)+2}{2^{n+1}} \\\\ \text{Ergebnis:}\\ && & \displaystyle 2- \frac{(n+1)+2}{2^{n+1}} = 2-\frac{(n+1)+2}{2^{n+1}}\ \checkmark \\ \hline \end{array}\)

Find the asymptote of -4x^2 + y^2 - 2y = 3 with positive slope. 

Enter your answer as an equation of the form y=mx+b.

Formula:
\(y^2 + Ax^2+Bx + Cxy +Dy + E = 0 \\ \text{$1.$ asymptote: $y = m_1x+b_1$} \\ \text{$2.$ asymptote: $y = m_2x+b_2$} \\ \begin{array}{|rcll|} \hline m_1 &=& \dfrac{-C+\sqrt{C^2-4A} }{2} \\ m_2 &=& \dfrac{-C-\sqrt{C^2-4A} }{2} \\ b_1 &=& \dfrac{B+m_1D}{m_2-m_1} \\ b_2 &=& -\dfrac{B+m_2D}{m_2-m_1} \\ \hline \end{array} \)

Equation of the hyperbola:  \(y^2 -4x^2 - 2y - 3 = 0\)

\(\begin{array}{|rcr|} \hline A &=& -4 \\ B &=& 0 \\ C &=& 0 \\ D &=& -2 \\ E &=& -3 \\ \hline \end{array} \begin{array}{|rcl|} \hline m_1 &=& \dfrac{-C+\sqrt{C^2-4A} }{2} \\ &=& \dfrac{0+\sqrt{0-4(-4)} }{2} \\ &=& \dfrac{ \sqrt{16} }{2} \\ &=& \dfrac{ 4 }{2} \\ \mathbf{m_1} & \mathbf{=} & \mathbf{2} \\ \hline m_2 &=& \dfrac{-C-\sqrt{C^2-4A} }{2} \\ &=& \dfrac{0-\sqrt{0-4(-4)} }{2} \\ &=& \dfrac{ -\sqrt{16} }{2} \\ &=& \dfrac{ -4 }{2} \\ \mathbf{m_2} & \mathbf{=} & \mathbf{-2} \\ \hline b_1 &=& \dfrac{B+m_1D}{m_2-m_1} \\ &=& \dfrac{0+2(-2)}{(-2)-2} \\ &=& \dfrac{-4}{-4} \\ \mathbf{b_1} & \mathbf{=} & \mathbf{1} \\ \hline b_2 &=& -\dfrac{B+m_2D}{m_2-m_1} \\ &=& -\dfrac{0+(-2)(-2)}{(-2)-2} \\ &=& -\dfrac{4}{-4} \\ \mathbf{b_2} & \mathbf{=} & \mathbf{1} \\ \hline \end{array}\)

\(\text{$1.$ Asymptote: $y = 2x + 1$ (positive slope )}\\ \text{$2.$ Asymptote: $y = -2x +1$ } \)

Define the function $g(x)=3x+2$. If $g(x)=2f^{-1}(x)$ and $f^{-1}(x)$ is the inverse of the function $f(x)=ax+b$, find $\dfrac{a+b}{2}$.

\(\begin{array}{|rcll|} \hline f(x) &=& ax+b \\ \hline y &=& ax+b \\\\ ax &=& y-b \\\\ x &=& \dfrac{y-b}{a} \quad & | \quad x \leftrightarrow y \\\\ y &=& \dfrac{x-b}{a} \\\\ \mathbf{f^{-1}(x)} &\mathbf{=}& \mathbf{\dfrac{x-b}{a}} \\ \hline g(x) &=& 3x+2 \\ g(x) &=& 2f^{-1}(x) \\ 3x+2 &=& 2\left( \dfrac{x-b}{a} \right) \\\\ \dfrac{3x+2}{2} &=& \dfrac{x-b}{a} \\\\ \mathbf{\dfrac{3}{2}x+1} &\mathbf{=}& \mathbf{\dfrac{1}{a}x-\dfrac{b}{a}} \quad & | \quad \text{compare} \\\\ \hline \dfrac{3}{2} &=& \dfrac{1}{a} \\ \mathbf{a} &\mathbf{=}& \mathbf{\dfrac{2}{3}} \\ \hline 1 &=& -\dfrac{b}{a} \\ \dfrac{b}{a} &=& -1 \\ b &=& -a \\ \mathbf{b} &\mathbf{=}& \mathbf{-\dfrac{2}{3}} \\ \hline \end{array} \)

\(\begin{array}{|rcll|} \hline \dfrac{a+b}{2} &=& \dfrac{ \dfrac{2}{3}-\dfrac{2}{3} }{2}\\\\ \mathbf{\dfrac{a+b}{2}} &\mathbf{=}& \mathbf{0} \\ \hline \end{array}\)

find the constant term in the expansion of (1 + x )^10(1+ 1/x)^12

\(\small{ \begin{array}{|rcll|} \hline && (1 + x )^{10} \left(1+ \dfrac{1}{x} \right)^{12} \\\\ &=& (1 + x )^{10}\left( \dfrac{1+x}{x} \right)^{12} \\\\ &=&\dfrac{(1 + x )^{10}(1 + x )^{12}}{x^{12}} \\\\ &=&\dfrac{(1 + x )^{22}}{x^{12}} \\\\ &=&\dfrac{ \binom{22}{0}x^0 +\binom{22}{1}x^1+ \binom{22}{2}x^2 + \ldots + \binom{22}{11}x^{11}+ \binom{22}{12}x^{12}+ \binom{22}{13}x^{13} + \ldots + \binom{22}{21}x^{21}+ \binom{22}{22}x^{22} }{x^{12}} \\\\ &=& \binom{22}{0}x^{-12} +\binom{22}{1}x^{-11}+ \binom{22}{2}x^{-10} + \ldots + \binom{22}{11}x^{-1}+\binom{22}{12}+ \binom{22}{13}x^{1} + \ldots + \binom{22}{21}x^{9}+ \binom{22}{22}x^{10} \\ \hline \end{array} }\)

The constant term is:

\(\begin{array}{|rcll|} \hline && \dbinom{22}{12} \\\\ &=& \dbinom{22}{22-12}\\ \\ &=& \dbinom{22}{10} \\\\ &\mathbf{=}& \mathbf{646646} \\ \hline \end{array}\)

A sequence of positive integers with a_1 = 1 and a_9 + a_{10} = 646 is formed so that the first three terms are in geometric progression, the second, third, and fourth terms are in arithmetic progression, and, in general, for all \(n\geq1\) , the terms, a_{2n-1}, a_{2n}, a_{2n + 1} are in geometric progression, and the terms, a_{2n}, a_{2n + 1}, and a_{2n + 2} , and  are in arithmetic progression. Let a_n be the greatest term in this sequence that is less than 1000. Find a_n.

The Fibonacci sequence, with \(F_0 = 0\), \(F_1 = 1\) and \(F_n = F_{n - 2} + F_{n - 1}\), had a closed form \(F_n = \frac{1}{\sqrt{5}} \left( \phi^n - \widehat{\phi}^n \right),\) where \(\phi = \frac{1 + \sqrt{5}}{2} \; \text{and} \; \widehat{\phi} = \frac{1 - \sqrt{5}}{2}.\) The Lucas numbers are defined in a similar way. Let \(L_0\) be the zeroth Lucas number and \(L_1\) be the first. If \(\begin{align*} L_0 &= 2 \\ L_1 &= 1 \\ L_n &= L_{n - 1} + L_{n - 2} \; \text{for}\; n \geq 2 \end{align*}\) Find \((a,b)\) such that \(L_n = a\phi^n + b\widehat{\phi}^n.\)

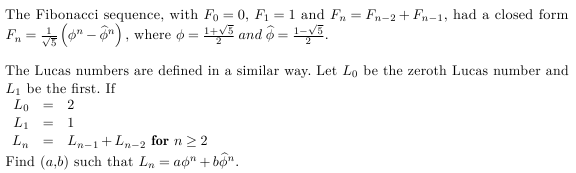
\(\text{Fibonacci sequence $0,1,1,2,3,5,8,13,21,34,55,\ldots$} \\ \begin{array}{|lcr|} \hline a_0 = a_0 &=& 0\cdot a_1 + 1 \cdot a_0 \\ a_1 = a_1 &=& 1\cdot a_1 + 0 \cdot a_0 \\ a_2 = a_1+a_0 &=& 1\cdot a_1 + 1 \cdot a_0 \\ a_3 = a_2+a_1 &=& 2\cdot a_1 + 1 \cdot a_0 \\ a_4 = a_3+a_2 &=& 3\cdot a_1 + 2 \cdot a_0 \\ a_5 = a_4+a_3 &=& 5\cdot a_1 + 3 \cdot a_0 \\ a_6 = a_5+a_4 &=& 8\cdot a_1 + 5 \cdot a_0 \\ a_7 = a_6+a_5 &=& 13\cdot a_1 + 8 \cdot a_0 \\ a_8 = a_7+a_6 &=& 21\cdot a_1 + 13 \cdot a_0 \\ \ldots \\ a_n = a_{n-1}+a_{n-2} &=& F_n\cdot a_1 + F_{n-1} \cdot a_0 \\ && \boxed{a_n = F_n\cdot a_1 + F_{n-1} \cdot a_0 } \\\\ \text{Lucas numbers:} \\ a_0 = L_0 = 2 \\ a_1 = L_1 = 1 \\ a_n = L_n =F_n\cdot 1 + F_{n-1} \cdot 2 \\ && \boxed{L_n =F_n + 2F_{n-1}} \\ \hline \end{array} \)

\(\begin{array}{|rcll|} \hline F_n &=& \frac{1}{\sqrt{5}} \left( \phi^n - \widehat{\phi}^n \right) \\ F_{n-1} &=& \frac{1}{\sqrt{5}} \left( \phi^{n-1} - \widehat{\phi}^{n-1} \right) \\ \boxed{L_n =F_n + 2F_{n-1}} \\ L_n &=& \frac{1}{\sqrt{5}} \left( \phi^n - \widehat{\phi}^n \right) + 2\frac{1}{\sqrt{5}} \left( \phi^{n-1} - \widehat{\phi}^{n-1} \right) \\ &=& \dfrac{ \left( \phi^n - \widehat{\phi}^n \right)+2\left( \phi^{n-1} - \widehat{\phi}^{n-1} \right) } { \sqrt{5} } \\ &=& \dfrac{ \phi^n - \widehat{\phi}^n+2 \phi^{n-1} - 2\widehat{\phi}^{n-1} } { \sqrt{5} } \\ &=& \dfrac{ \phi^n+2 \phi^{n-1} - \widehat{\phi}^n - 2\widehat{\phi}^{n-1} } { \sqrt{5} } \\ &=& \dfrac{ \phi^n\left( 1+\dfrac{2}{\phi} \right) - \widehat{\phi}^n\left( 1+\dfrac{2}{\widehat{\phi}} \right) }{ \sqrt{5} } \quad | \quad \frac{1}{\phi} = \phi -1 \quad \frac{1}{\widehat{\phi}} = \widehat{\phi} -1 \\ &=& \dfrac{ \phi^n\Big( 1+2(\phi -1 ) \Big) - \widehat{\phi}^n\left( 1+2(\widehat{\phi} -1) \right) }{ \sqrt{5} } \\ &=& \dfrac{ \phi^n( 2\phi -1 ) - \widehat{\phi}^n\left( 2\widehat{\phi} -1 \right) }{ \sqrt{5} } \quad | \quad 2\phi -1 = \sqrt{5} \quad 2\widehat{\phi} -1= -\sqrt{5} \\ &=& \dfrac{ \phi^n\sqrt{5} - \widehat{\phi}^n\left( -\sqrt{5} \right) }{ \sqrt{5} } \\ &=& \dfrac{ \phi^n\sqrt{5} + \widehat{\phi}^n \sqrt{5} } { \sqrt{5} } \\ &=& \phi^n + \widehat{\phi}^n \\ \boxed{L_n =\phi^n + \widehat{\phi}^n } \\ \hline \end{array}\)

(a,b) = (1,1)
 

Suppose that $f(x)=\frac{1}{2x+b}$. For what value of $b$ does $f^{-1}(x)=\frac{1-2x}{2x}$?

\(\begin{array}{|rcll|} \hline f(x) &=& \dfrac{1}{2x+b} \\ \hline y &=& \dfrac{1}{2x+b} \\\\ \dfrac{1}{y} &=& 2x+b \\\\ 2x &=& \dfrac{1}{y}-b \\\\ x &=& \dfrac{\dfrac{1}{y}-b}{2} \quad & | \quad x \leftrightarrow y \\\\ y &=& \dfrac{\dfrac{1}{x}-b}{2} \\\\ f^{-1}(x) &=& \dfrac{\dfrac{1}{x}-b}{2} \\ \hline f^{-1}(x) = \dfrac{\dfrac{1}{x}-b}{2} &=& \dfrac{1-2x}{2x} \\\\ \dfrac{\dfrac{1}{x}-b}{2} &=& \dfrac{1-2x}{2x} \\\\ \dfrac{1}{x}-b &=& \dfrac{1-2x}{x} \\\\ \dfrac{1}{x}-b &=& \dfrac{1}{x}-2 \\\\ -b &=& -2 \\\\ \mathbf{b} & \mathbf{=}& \mathbf{2} \\ \hline \end{array}\)

The diagonals of a trapezoid are perpendicular and have lengths 8 and 10.

Find the length of the median of the trapezoid.

Area A = ?

\(\begin{array}{|rcll|} \hline 2A &=& (8-y)x + xy + (10-x)y+(10-x)(8-y) \\ 2A &=& 8x-yx+xy+10y-xy+80-10y-8x+xy \\ 2A &=& 80 \\ \mathbf{A} & \mathbf{=} & \mathbf{40} \\ \hline \end{array}\)

h = ?

\(\begin{array}{|rclrcl|} \hline \sin(B) &=& \dfrac{h}{8} & \sin(A) &=& \dfrac{h}{10} \quad & | \quad B = 90^{\circ}-A \\ \sin(90^{\circ}-A)^2+ \sin(A)^2 &=& \dfrac{h^2}{8^2} +\dfrac{h^2}{10^2} \\ \cos(A)^2+ \sin(A)^2 &=& \dfrac{h^2}{8^2} +\dfrac{h^2}{10^2} \\ 1 &=& \dfrac{h^2}{8^2} +\dfrac{h^2}{10^2} \\ \dfrac{h^2}{8^2} +\dfrac{h^2}{10^2} &=& 1 \\ h^2\left( \dfrac{1}{8^2} + \dfrac{1}{10^2} \right) &=& 1 \\ h^2\left( \dfrac{164}{8^210^2} \right) &=& 1 \\ h &=& \dfrac{8\cdot 10}{\sqrt{164}} \\ h &=& \dfrac{8\cdot 10}{\sqrt{4\cdot 41}} \\ h &=& \dfrac{8\cdot 10}{2\sqrt{41}} \\ \mathbf{ h }&\mathbf{=}& \mathbf{\dfrac{40}{\sqrt{41}} } \\ \hline \end{array}\)

median m = ?

\(\begin{array}{|rcll|} \hline A &=& \dfrac{a+c}{2} \cdot h \quad & | \quad m = \dfrac{a+c}{2}\\\\ A &=& m \cdot h \\\\ m &=& \dfrac{A}{h} \\\\ m &=& \dfrac{40}{ \dfrac{40}{\sqrt{41} } } \\\\ m &=& \dfrac{40}{40}\cdot \sqrt{41} \\\\ m &=& \sqrt{41} \\\\ \mathbf{ m} &\mathbf{ =} & \mathbf{ 6.40312423743} \\ \hline \end{array} \)