We have a parabola with equation
\(y=-2{x^2}+8x+10\),
and a hyperbola with equation
\(xy=16\)
We have to solve \(\mathbf{ x^3-4x^2-5x +8=0}\)
1.
We attempt x = 1
\(\begin{array}{|rcll|} \hline \mathbf{ x^3-4x^2-5x+8} &\mathbf{=}& \mathbf{0} \quad | \quad x=1 \\\\ 1^3-4\cdot 1^2-5\cdot 1 +8 &\overset{?}{=} & 0 \\ 1 -4 -5 +8 &\overset{?}{=} & 0 \\ 9-9 &\overset{?}{=} & 0 \\ 0 & = & 0\ \checkmark \\ \hline \end{array}\)
We have found the first root, it is \( x = 1 \quad (1.\text{ quadrant })\)
\(\begin{array}{|rcll|} \hline x^3-4x^2-5x+8 = ( ~?~ )(x-1) \\ (x^3-4x^2-5x+8) : (x-1) = ( ~?~ ) \\ \hline \end{array} \)
2.
Polynomial long division:
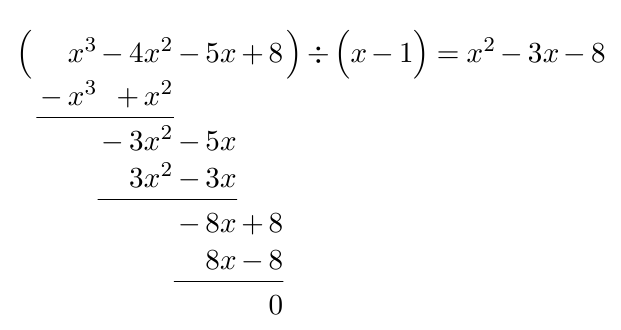
\(\begin{array}{|rcll|} \hline x^3-4x^2-5x+8 = ( x^2 - 3x-8 )(x-1) &=& 0 \\\\ x^2 - 3x -8 &=& 0 \\ x &=& \dfrac{3 \pm \sqrt{3^2-4(-8) } } {2} \\ x &=& \dfrac{3 \pm \sqrt{9+32} } {2} \\ x &=& \dfrac{3 \pm \sqrt{41} } {2} \\\\ x_2 &=& \dfrac{3 + \sqrt{41} } {2} \\ x_2 &=& 4.70156211872 \quad | \quad 1.\text{ quadrant } \\\\ x_3 &=& \dfrac{3 - \sqrt{41} } {2} \\ \mathbf{ x_3 } &\mathbf{=}& \mathbf{-1.70156211872} \quad | \quad 3.\text{ quadrant } \\\\ y_3 &=& \dfrac{16}{x_3} \\ y_3 &=& \dfrac{16}{-1.70156211872} \\ \mathbf{ y_3 } &\mathbf{=}& \mathbf{-9.40312423743} \\ \hline \end{array}\)
The point of intersection in the 3th quadrant is \(\mathbf{(-1.70156211872, -9.40312423743)}\)
