heureka

16.

In ABC with a right angle at C,

point D lies in the interior of AB and

point E lies in the interior of BC so that

AC=CD, DE=EB, and the ratio AC:DE = 4:3.

What is the ratio AD:DB?

$\text{Let $\overline{AC} = \overline{CD} = {\color{red}x} $ } \\ \text{Let $\overline{DE} = \overline{EB} = {\color{red}y} $ } \\ \text{Let $\overline{AD} = {\color{red}s} $ } \\ \text{Let $\overline{DB} = {\color{red}t} $ }$

$\text{Let $\angle{CAD} = \angle{ADC} = \alpha $ } \\ \text{Let $\angle{ABC} = \angle{EDB} = 90^{\circ}-\alpha $ } \\ \text{Let $\angle{DCA} = 180^{\circ}-2\alpha $ } \\ \text{Let $\angle{ECD} = 90^{\circ}-\angle{DCA} = 90^{\circ} -(180^{\circ}-2\alpha) = 2\alpha-90^{\circ} $ } \\ \text{Let $\angle{BED} = 180^{\circ}-2(90^{\circ}-\alpha)=2\alpha $ } \\ \text{Let $\angle{DEC} = 180^{\circ}-\angle{BED}=180^{\circ}-2\alpha $ }$

$\begin{array}{|rcll|} \hline \angle{CDE} &=& 180^{\circ}- \angle{ECD}-\angle{DEC} \\ &=& 180^{\circ}-(2\alpha-90^{\circ})- (180^{\circ}-2\alpha ) \\ &\mathbf{=}& \mathbf{90^{\circ} \ !} \\ \hline \end{array}$

$\mathbf{\text{$\cos$-rule in $\triangle ACD$}}$

$\begin{array}{|rcll|} \hline x^2 &=& x^2+s^2-2xs\cos(\alpha) \\ 2xs\cos(\alpha) &=& s^2 \\ \mathbf{2x\cos(\alpha)} & \mathbf{=} & \mathbf{s} \quad & (1) \\ \hline \end{array}$

$\mathbf{\text{$\cos$-rule in $\triangle DEB$}}$

$\begin{array}{|rcll|} \hline y^2 &=& y^2+t^2-2yt\cos(90^{\circ}-\alpha) \\ 2yt\sin(\alpha) &=& t^2 \\ \mathbf{2y\sin(\alpha)} & \mathbf{=} & \mathbf{t} \quad & (2) \\ \hline \end{array}$

$\begin{array}{|lrcll|} \hline \dfrac{(1)}{(2)}: & \dfrac{ 2x\cos(\alpha) } {2y\sin(\alpha) } &=& \dfrac{ s }{t} \\ \\ & \dfrac{x}{y} \cdot \dfrac{ \cos(\alpha) } {\sin(\alpha) } &=& \dfrac{ s }{t} \\ \\ & \mathbf{ \dfrac{x}{y} \cdot \dfrac{ 1 } {\tan(\alpha) }} & \mathbf{=} & \mathbf{\dfrac{ s }{t}} \quad & (3) \\ \hline \end{array}$

$\mathbf{\text{In the right-angled $\triangle DCE$}} \\ \mathbf{ \tan(\alpha) =\ ?}$

$\begin{array}{|rcll|} \hline \tan(180^{\circ}-2\alpha) &=& \dfrac{x}{y} \\\\ -\tan(2\alpha) &=& \dfrac{4}{3} \quad | \quad \text{Formula:} \ \boxed{ \tan(2\alpha)=\dfrac{2\tan{\alpha}}{1-\tan^2(\alpha)} } \\\\ \dfrac{-2\tan{\alpha}}{1-\tan^2(\alpha)} &=& \dfrac{4}{3} \\\\ \dfrac{2\tan{\alpha}}{\tan^2(\alpha)-1} &=& \dfrac{4}{3} \\\\ \dfrac{ \tan{\alpha}}{\tan^2(\alpha)-1} &=& \dfrac{2}{3} \\\\ 3\tan{\alpha} &=& 2(\tan^2(\alpha)-1) \\ 3\tan{\alpha} &=& 2\tan^2(\alpha)-2 \\ 2\tan^2(\alpha)-3\tan(\alpha)-2 &=& 0 \\\\ \tan(\alpha)&=& \dfrac{3\pm \sqrt{9-2\cdot4\cdot(-2)}} {2\cdot 2} \\\\ \tan(\alpha)&=& \dfrac{3\pm \sqrt{25}} {4} \\\\ \tan(\alpha)&=& \dfrac{3\pm 5} {4} \\\\ \tan(\alpha)&=& \dfrac{3 {\color{red}+} 5} {4} \quad | \quad \tan(\alpha) > 0\ ! \\\\ \tan(\alpha)&=& \dfrac{8} {4} \\ \mathbf{ \tan(\alpha) }& \mathbf{=} & \mathbf{2} \\ \hline \end{array}$

$\begin{array}{|rcll|} \hline \mathbf{ \dfrac{x}{y} \cdot \dfrac{ 1 } {\tan(\alpha) }} & \mathbf{=} & \mathbf{\dfrac{ s }{t}} \quad | \quad \mathbf{\tan(\alpha)=2},\ \quad \dfrac{x}{y}=\dfrac{4}{3} \\\\ \dfrac{4}{3} \cdot \dfrac{1} {2} & = & \dfrac{ s }{t} \\\\ \dfrac{4}{6} & = & \dfrac{ s }{t} \\\\ \dfrac{2}{3} & = & \dfrac{ s }{t} \\\\ \mathbf{\dfrac{ s }{t}} &\mathbf{=}& \mathbf{\dfrac{2}{3}} \\ \hline \end{array}$

$(A) \ 2:3$

Please help

I can't give you a detailed solution, but i give you the solution by wolfram alpha:

WolframAlpha: solve  y^2-zx = -103, z^2-xy = 22, x^2-yz > 81 over the positive integers

So $x^2-yz = 14^2-3\cdot 8 = 172$

How do i get this $x^2-yz > 81$ ?

$\begin{array}{|rcll|} \hline && (x^2-yz) + (y^2-zx) + (z^2-xy) \\ &=& x^2+y^2+z^2-yz-zx-xy \\\\ &=& \dfrac{1}{2}(2x^2+2y^2+2z^2-2yz-2zx-2xy) \\\\ &=& \dfrac{1}{2}\left( (x^2-2xy+y^2) + (y^2-2yz+z^2) + (z^2-2zx+x^2) \right) \\ &=& \dfrac{1}{2}\left( (x-y)^2 + (y-z)^2 + (z-x)^2 \right) \quad | \quad \text{this is always positive} \\\\ (x^2-yz) + (y^2-zx) + (z^2-xy) &>& 0 \\ (x^2-yz) -103 + 22 &>& 0 \\ (x^2-yz) -81 &>& 0 \\ \mathbf{x^2-yz} & \mathbf{>} & \mathbf{81} \\ \hline \end{array}$

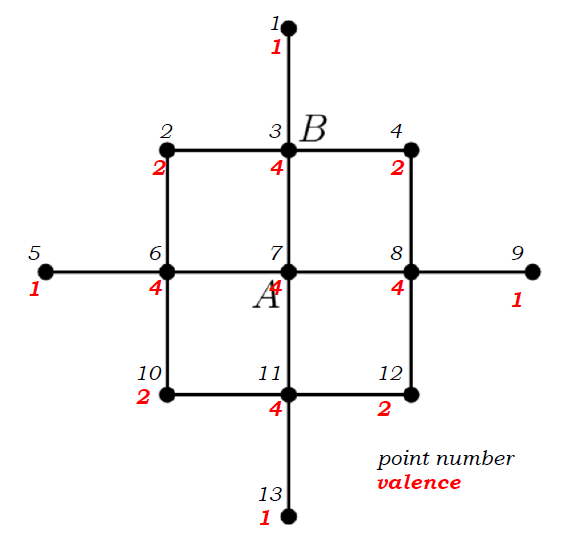
An ant moves on the following lattice, beginning at the dot labeled A.
Each minute he moves to one of the dots neighboring the dot he was at, choosing from among its neighbors at random.
What is the probability that after 5 minutes he is at the dot labeled B ?

My attempt:

$\begin{array}{|r|r|r|} \hline & \text{path} & \text{probability} & \text{probability} \\ \hline 1& 3,2,3,2,3,&0.0039062500 \\ 2& 3,2,3,4,3,&0.0039062500\\ 3& 3,2,3,7,3,&0.0019531250\\ 4& 3,2,3,1,3,&0.0078125000 \\ 5& 3,2,6,2,3,&0.0039062500 \\ 6& 3,2,6,7,3,&0.0019531250 \\ 7& 3,4,3,2,3,&0.0039062500 \\ 8& 3,4,3,4,3,&0.0039062500 \\ 9& 3,4,3,7,3,&0.0019531250 \\ 10& 3,4,3,1,3,&0.0078125000 \\ 11& 3,4,8,4,3,&0.0039062500 \\ 12& 3,4,8,7,3,&0.0019531250 \\ 13& 3,7,3,2,3,&0.0019531250 \\ 14& 3,7,3,4,3,&0.0019531250 \\ 15& 3,7,3,7,3,&0.0009765625 \\ 16& 3,7,3,1,3,&0.0039062500 \\ 17& 3,7,6,2,3,&0.0019531250 \\ 18& 3,7,6,7,3,&0.0009765625 \\ 19& 3,7,8,4,3,&0.0019531250 \\ 20& 3,7,8,7,3,&0.0009765625 \\ 21& 3,7,11,7,3,&0.0009765625 \\ 22& 3,1,3,2,3,&0.0078125000 \\ 23& 3,1,3,4,3,&0.0078125000 \\ 24& 3,1,3,7,3,&0.0039062500 \\ 25& 3,1,3,1,3,&0.0156250000 \\ 26& 6,2,3,2,3,&0.0039062500 \\ 27& 6,2,3,4,3,&0.0039062500 \\ 28& 6,2,3,7,3,&0.0019531250 \\ 29& 6,2,3,1,3,&0.0078125000 \\ 30& 6,2,6,2,3,&0.0039062500 \\ 31& 6,2,6,7,3,&0.0019531250 \\ 32& 6,5,6,2,3,&0.0078125000 \\ 33& 6,5,6,7,3,&0.0039062500 \\ 34& 6,7,3,2,3,&0.0019531250 \\ 35& 6,7,3,4,3,&0.0019531250 \\ 36& 6,7,3,7,3,&0.0009765625 \\ 37& 6,7,3,1,3,&0.0039062500 \\ 38& 6,7,6,2,3,&0.0019531250 \\ 39& 6,7,6,7,3,&0.0009765625 \\ 40& 6,7,8,4,3,&0.0019531250 \\ 41& 6,7,8,7,3,&0.0009765625 \\ 42& 6,7,11,7,3,&0.0009765625 \\ 43& 6,10,6,2,3,&0.0039062500 \\ 44& 6,10,6,7,3,&0.0019531250 \\ 45& 6,10,11,7,3,&0.0019531250 \\ 46& 8,4,3,2,3,&0.0039062500 \\ 47& 8,4,3,4,3,&0.0039062500 \\ 48& 8,4,3,7,3,&0.0019531250 \\ 49& 8,4,3,1,3,&0.0078125000 \\ 50& 8,4,8,4,3,&0.0039062500 \\ 51& 8,4,8,7,3,&0.0019531250 \\ 52& 8,7,3,2,3,&0.0019531250 \\ 53& 8,7,3,4,3,&0.0019531250 \\ 54& 8,7,3,7,3,&0.0009765625 \\ 55& 8,7,3,1,3,&0.0039062500 \\ 56& 8,7,6,2,3,&0.0019531250 \\ 57& 8,7,6,7,3,&0.0009765625 \\ 58& 8,7,8,4,3,&0.0019531250 \\ 59& 8,7,8,7,3,&0.0009765625 \\ 60& 8,7,11,7,3,&0.0009765625 \\ 61& 8,9,8,4,3,&0.0078125000 \\ 62& 8,9,8,7,3,&0.0039062500 \\ 63& 8,12,8,4,3,&0.0039062500 \\ 64& 8,12,8,7,3,&0.0019531250 \\ 65& 8,12,11,7,3,&0.0019531250 \\ 66& 11,7,3,2,3,&0.0019531250 \\ 67& 11,7,3,4,3,&0.0019531250 \\ 68& 11,7,3,7,3,&0.0009765625 \\ 69& 11,7,3,1,3,&0.0039062500 \\ 70& 11,7,6,2,3,&0.0019531250 \\ 71& 11,7,6,7,3,&0.0009765625 \\ 72& 11,7,8,4,3,&0.0019531250 \\ 73& 11,7,8,7,3,&0.0009765625 \\ 74& 11,7,11,7,3,&0.0009765625 \\ 75& 11,10,6,2,3,&0.0039062500 \\ 76& 11,10,6,7,3,&0.0019531250 \\ 77& 11,10,11,7,3,&0.0019531250 \\ 78& 11,12,8,4,3,&0.0039062500 \\ 79& 11,12,8,7,3,&0.0019531250 \\ 80& 11,12,11,7,3,&0.0019531250 \\ 81& 11,13,11,7,3,&0.0039062500& \text{sum } = 0.2500000000 \\ \hline \end{array}$

The probability that after 5 minutes he is at the dot labeled B is $0.25\ (25\ \%)$

There are two points, A and B.

The point A is (1,1) and point B is (5,6)

Point P is along the line segment of AB, and it makes a ratio of AP to BP to 1:2. 

What is point P?

Round to tenth decimal

$\begin{array}{|rcll|} \hline \vec{P} &=& \vec{A}+ \lambda \left( \vec{B}-\vec{A} \right) \quad | \quad \lambda = \dfrac{1}{1+2} = \dfrac{1}{3} \\\\ \vec{P} &=& \vec{A}+ \dfrac{1}{3}\left( \vec{B}-\vec{A} \right) \quad | \quad \vec{A}=\dbinom{1}{1},\ \vec{B}=\dbinom{5}{6} \\\\ \vec{P} &=& \dbinom{1}{1}+ \dfrac{1}{3}\left( \dbinom{5}{6}-\dbinom{1}{1} \right) \\\\ \vec{P} &=& \dbinom{1}{1}+ \dfrac{1}{3} \dbinom{5-1}{6-1} \\\\ \vec{P} &=& \dbinom{1}{1}+ \dfrac{1}{3} \dbinom{4}{5} \\\\ \vec{P} &=& \dbinom{1+\frac{4}{3}}{1+\frac{5}{3}} \\\\ \vec{P} &=& \dbinom{ \frac{7}{3}}{ \frac{8}{3}} \\\\ \mathbf{\vec{P}} & \mathbf{=} & \mathbf{\dbinom{2.3}{2.7}} \\ \hline \end{array}$

P = (2.3, 2.7)

Given that (2,3) is on the graph of y=f(x), find a point on the graph of y=f(2x+1)+3. 

Express your answer as an ordered pair (a,b) where a and b are real numbers.

$\begin{array}{|rcll|} \hline y &=& f(x) \quad | \quad (x=2,\ y= 3 )\\ 3 &=& f(2) \\ \mathbf{f(2)} & \mathbf{=} & \mathbf{3} \\ \hline \end{array}$

$\begin{array}{|rcll|} \hline y &=& f(2x+1)+3 \\\\ 2x+1 &=& 2 \\ 2x &=& 1 \\ \mathbf{x} & \mathbf{=} & \mathbf{\dfrac{1}{2}} \\\\ y &=& f(2) + 3 \quad | \quad \mathbf{f(2)=3} \\ y &=& 3 + 3 \\ \mathbf{y} & \mathbf{=} & \mathbf{6} \\ \hline \end{array}$

$(a,b) = \left( \dfrac{1}{2},\ 6 \right)$

[x/2]+[x/4]+[x/8]+507=x

[x/2]+[x/4]+[x/8]+507=x

[x/2],[x/4],[x/8]- INTEGER DIVISIONS!!!

I assume the "Floor Function": $\left\lfloor\dfrac{x}{2}\right\rfloor+\left\lfloor\dfrac{x}{4}\right\rfloor+\left\lfloor\dfrac{x}{8}\right\rfloor+507=x$

So x is an integer.

We rearrange:

$\left\lfloor\dfrac{4x}{8}\right\rfloor+\left\lfloor\dfrac{2x}{8}\right\rfloor+\left\lfloor\dfrac{x}{8}\right\rfloor+507=x$

We substitute: $y= \dfrac{x}{8}$
$\left\lfloor 4y \right\rfloor+\left\lfloor 2y \right\rfloor+\left\lfloor y \right\rfloor+507=x$

$\text{The fractional part of $\mathbf{y}$ is $\alpha$ and $0 < \alpha < 1$ } \\ \text{The integer part of $\mathbf{y}$ is $n$ }\\ \text{So $\mathbf{y = n+\alpha}$} \\ \text{$\mathbf{x = \lfloor 8y \rfloor} = \lfloor 8(n+\alpha)\rfloor=8n+\lfloor 8\alpha\rfloor$}$

$\begin{array}{|rcll|} \hline \left\lfloor 4(n+\alpha)\right\rfloor+\left\lfloor 2(n+\alpha) \right\rfloor+\left\lfloor n+\alpha\right\rfloor+507 &=& 8n+\lfloor 8\alpha\rfloor \\\\ \mathbf{\left\lfloor 4n+4\alpha\right\rfloor+\left\lfloor 2n+2\alpha \right\rfloor+\left\lfloor n+\alpha \right\rfloor+507}&\mathbf{=}& \mathbf{8n+\lfloor 8\alpha\rfloor} \\ \hline \end{array}$

We divide alpha into 8 parts: 

$0 < \alpha < \frac{1}{8},\ \frac{1}{8} \le \alpha < \frac{2}{8},\ \frac{2}{8} \le \alpha < \frac{3}{8},\ \frac{3}{8} \le \alpha < \frac{4}{8} ,\ \frac{4}{8} \le \alpha < \frac{5}{8},\ \frac{5}{8} \le \alpha < \frac{6}{8},\ \frac{6}{8} \le \alpha < \frac{7}{8},\ \frac{7}{8} \le \alpha < \frac{8}{8}$

$\begin{array}{|r|r|rcl|} \hline \text{part} & \text{domain} & \\ \hline 1. & 0 < \alpha < \frac{1}{8} & \left\lfloor 4n+4\alpha\right\rfloor+\left\lfloor 2n+2\alpha \right\rfloor+\left\lfloor n+\alpha \right\rfloor+507& =& 8n+\lfloor 8\alpha\rfloor \\ && 4n +2n+n+507 &=& 8n+0 \\ && n &=& 507 \\ && x &=& 8n + \lfloor 8\alpha\rfloor \\ && x &=& 8\cdot 507 \\ && \mathbf{x} & \mathbf{=} & \mathbf{4056} \\ \hline 2. & \frac{1}{8} \le \alpha < \frac{2}{8} & \left\lfloor 4n+4\alpha\right\rfloor+\left\lfloor 2n+2\alpha \right\rfloor+\left\lfloor n+\alpha \right\rfloor+507& =& 8n+\lfloor 8\alpha\rfloor \\ && 4n +2n+n+507 &=& 8n+1 \\ && n &=& 506 \\ && x &=& 8n + \lfloor 8\alpha\rfloor \\ && x &=& 8\cdot 506+1 \\ && \mathbf{x} & \mathbf{=} & \mathbf{4049} \\ \hline 3. & \frac{2}{8} \le \alpha < \frac{3}{8} & \left\lfloor 4n+4\alpha\right\rfloor+\left\lfloor 2n+2\alpha \right\rfloor+\left\lfloor n+\alpha \right\rfloor+507& =& 8n+\lfloor 8\alpha\rfloor \\ && 4n +1+2n+n+507 &=& 8n+2 \\ && n &=& 506 \\ && x &=& 8n + \lfloor 8\alpha\rfloor \\ && x &=& 8\cdot 506+2 \\ && \mathbf{x} & \mathbf{=} & \mathbf{4050} \\ \hline 4. & \frac{3}{8} \le \alpha < \frac{4}{8} & \left\lfloor 4n+4\alpha\right\rfloor+\left\lfloor 2n+2\alpha \right\rfloor+\left\lfloor n+\alpha \right\rfloor+507& =& 8n+\lfloor 8\alpha\rfloor \\ && 4n +1+2n+n+507 &=& 8n+3 \\ && n &=& 505 \\ && x &=& 8n + \lfloor 8\alpha\rfloor \\ && x &=& 8\cdot 505+3 \\ && \mathbf{x} & \mathbf{=} & \mathbf{4043} \\ \hline 5. & \frac{4}{8} \le \alpha < \frac{5}{8} & \left\lfloor 4n+4\alpha\right\rfloor+\left\lfloor 2n+2\alpha \right\rfloor+\left\lfloor n+\alpha \right\rfloor+507& =& 8n+\lfloor 8\alpha\rfloor \\ && 4n +2+2n+1+n+507 &=& 8n+4 \\ && n &=& 506 \\ && x &=& 8n + \lfloor 8\alpha\rfloor \\ && x &=& 8\cdot 506+4 \\ && \mathbf{x} & \mathbf{=} & \mathbf{4052} \\ \hline 6. & \frac{5}{8} \le \alpha < \frac{6}{8} & \left\lfloor 4n+4\alpha\right\rfloor+\left\lfloor 2n+2\alpha \right\rfloor+\left\lfloor n+\alpha \right\rfloor+507& =& 8n+\lfloor 8\alpha\rfloor \\ && 4n +2+2n+1+n+507 &=& 8n+5 \\ && n &=& 505 \\ && x &=& 8n + \lfloor 8\alpha\rfloor \\ && x &=& 8\cdot 505+5 \\ && \mathbf{x} & \mathbf{=} & \mathbf{4045} \\ \hline 7. & \frac{6}{8} \le \alpha < \frac{7}{8} & \left\lfloor 4n+4\alpha\right\rfloor+\left\lfloor 2n+2\alpha \right\rfloor+\left\lfloor n+\alpha \right\rfloor+507& =& 8n+\lfloor 8\alpha\rfloor \\ && 4n +3+2n+1+n+507 &=& 8n+6 \\ && n &=& 505 \\ && x &=& 8n + \lfloor 8\alpha\rfloor \\ && x &=& 8\cdot 505+6 \\ && \mathbf{x} & \mathbf{=} & \mathbf{4046} \\ \hline 8. & \frac{7}{8} \le \alpha < \frac{8}{8} & \left\lfloor 4n+4\alpha\right\rfloor+\left\lfloor 2n+2\alpha \right\rfloor+\left\lfloor n+\alpha \right\rfloor+507& =& 8n+\lfloor 8\alpha\rfloor \\ && 4n +3+2n+1+n+507 &=& 8n+7 \\ && n &=& 504 \\ && x &=& 8n + \lfloor 8\alpha\rfloor \\ && x &=& 8\cdot 504+7 \\ && \mathbf{x} & \mathbf{=} & \mathbf{4039} \\ \hline \end{array}$

Image is question pls help me

Thanks, CPhill

Consider

$\text{points $A$,$B$ and $P$ in the picture below, with $\angle APB$ a right angle:}$

$\text{Then $\overrightarrow{AP}$ is the projection of $\overrightarrow{AB}$ onto some vector $u$ , } \\ \text{with $\mathbf{\vec{u} = \begin{pmatrix} 2 \\ 1 \end{pmatrix} }$ } \\ \text{If $u_1 + u_2 = 3$, what is $\vec{u}$? } \\ \text{Let $\vec{AB} = \dbinom{2}{5}$ } \\ \text{Let $\vec{AP} = \dbinom{x_p}{y_p}$ } \\ \text{Let line $\overline{AP}:\quad y = \dfrac{1}{2}x$ }$

$\mathbf{\vec{AP} = \ ? }$

$\begin{array}{|rcll|} \hline \overline{AB}^2 &=& 2^2 + 5^2 \\ &=& 29 \\ \overline{AP}^2 &=& x_p^2+y_p^2 \\ \overline{BP}^2 &=& (2-x_p)^2+(5-y_p)^2 \\ \overline{AP}^2 + \overline{BP}^2 &=& \overline{AB}^2 \\ x_p^2+y_p^2 + (2-x_p)^2+(5-y_p)^2 &=& 29 \\ x_p^2+y_p^2 + 4-4x_p+x_p^2+25-10y_p+y_p^2 &=& 29 \\ 2x_p^2+2y_p^2 -4x_p -10y_p+29 &=& 29 \\ 2x_p^2+2y_p^2 -4x_p -10y_p &=& 0 \quad | \quad : 2 \\ x_p^2+y_p^2 -2x_p -5y_p &=& 0 \quad | \quad y_p = \dfrac{1}{2}x_p \\ x_p^2+\dfrac{1}{4}x_p^2 -2x_p -5(\dfrac{1}{2}x_p) &=& 0 \quad | \quad : x_p \\ x_p +\dfrac{1}{4}x_p -2 -\dfrac{5}{2} &=& 0 \\ \dfrac{5}{4}x_p &=& \dfrac{9}{2} \\ \mathbf{ x_p } & \mathbf{=} & \mathbf{\dfrac{18}{5}} \\\\ y_p &=& \dfrac{1}{2}x_p \\ y_p &=& \dfrac{1}{2}\cdot\dfrac{18}{5} \\ \mathbf{ y_p } & \mathbf{=} & \mathbf{\dfrac{9}{5}} \\ \mathbf{\vec{AP}} &\mathbf{=}& \mathbf{\dfrac{9}{5}\dbinom{2}{1}} \\ \hline \end{array}$

$\text{Let $\vec{u} = \dbinom{u_1}{u_2}$ } \\ \text{Let $u^2 = u_1^2+u_2^2$ }$

$\begin{array}{|rcll|} \hline \dfrac{(\vec{u}\cdot \vec{AB})\cdot \vec{u}}{u^2} &=& \vec{AP} \\\\ \dfrac{\left(\dbinom{u_1}{u_2}\cdot \dbinom{2}{5}\right)\cdot \dbinom{u_1}{u_2}}{u_1^2+u_2^2} &=& \dfrac{9}{5}\dbinom{2}{1} \\\\ \dbinom{ \left( 2u_1+5u_2\right)\cdot \dfrac{u_1}{u_1^2+u_2^2} } { \left( 2u_1+5u_2\right)\cdot \dfrac{u_2}{u_1^2+u_2^2} } &=& \dfrac{9}{5}\dbinom{2}{1} \\\\ ( 2u_1+5u_2)\cdot \dfrac{u_1}{u_1^2+u_2^2} &=& \dfrac{18}{5} \\\\ 5( 2u_1+5u_2)\cdot u_1 &=& 18(u_1^2+u_2^2) \\ 5( 2u_1^2+5u_1u_2) &=& 18u_1^2+18u_2^2 \\ 10u_1^2+25u_1u_2 &=& 18u_1^2+18u_2^2 \quad | \quad u_2 = 3-u_1 \\ 10u_1^2+25u_1(3-u_1) &=& 18u_1^2+18(3-u_1)^2 \\ 10u_1^2+75u_1-25u_1^2 &=& 18u_1^2+162-108u_1+18u_1^2 \\ 51u_1^2-183u_1 + 162 &=& 0 \quad | \quad : 3 \\ 17u_1^2-61u_1 + 54 &=& 0 \\\\ u_1 &=& \dfrac{61\pm \sqrt{61^2-4\cdot 17 \cdot 54}}{2\cdot 17} \\ u_1 &=& \dfrac{61\pm \sqrt{49}}{34} \\ u_1 &=& \dfrac{61\pm 7}{34} \\\\ \hline u_1 &=& \dfrac{61+7}{34} \\ u_1 &=& \dfrac{68}{34} \\ \mathbf{u_1} & \mathbf{=} & \mathbf{2} \\\\ \quad u_2 &=& 3 - u_1 \\ \quad u_2 &=& 3 - 2 \\ \quad \mathbf{u_2} &\mathbf{=}& \mathbf{1} \quad | \quad \dfrac{u_2}{u_1} = \dfrac{1}{2} \ \checkmark \\ \hline u_1 &=& \dfrac{61-7}{34} \\ u_1 &=& \dfrac{27}{17} \\ \quad u_2 &=& 3 - u_1 \\ \quad u_2 &=& 3 - \dfrac{27}{17} \\ \quad u_2 &=& \dfrac{24}{17} \quad | \quad \dfrac{u_2}{u_1} = \dfrac{24}{27} \ne \dfrac{1}{2} \\ \hline \end{array}$

$\mathbf{\vec{u} = \begin{pmatrix} 2 \\ 1 \end{pmatrix} }$