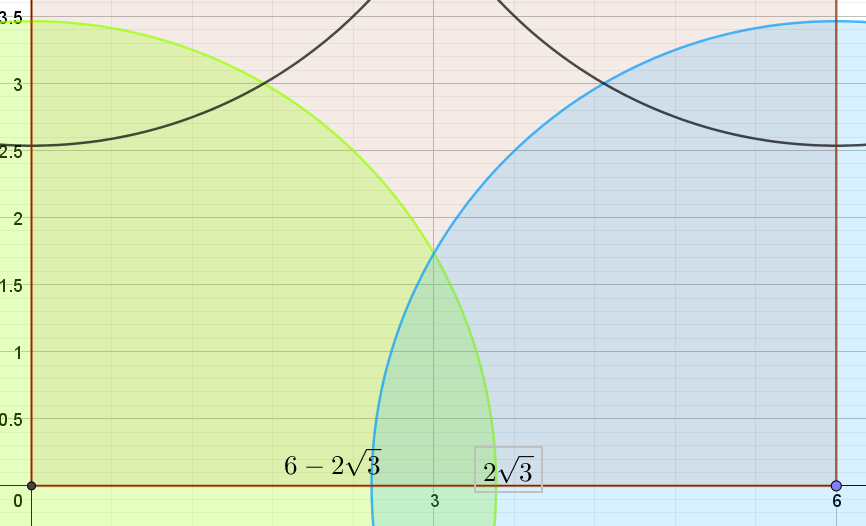
The area of the whole square is 36
the area of tone quadrant = \(0.25 \pi r^2= 0.25*\pi*(2\sqrt3)^2=3\pi\;\;cm^2\)
Let the bottom of this diagram be the x- axis.
and (0,0) is at the bottom left corner then the equation of the bottom left quadrant is
\(x^2+y^2=12\\ y^2=12-x^2\\ y=\sqrt{12-x^2}\)
The area of the blue/ green overlap is
\(A=\displaystyle 2\int_3^{2\sqrt3}\;\;\sqrt{12-x^2}\;\;dx\\ =2\left[ 0.5x\sqrt{12-x^2}+6 * asin(\frac{x}{2\sqrt3} ) \right]_3^{2\sqrt3} \qquad \text{Wolfram|Alpha}\\ =2\left[ 0.5(2\sqrt3)\sqrt{0}+6 * asin(1 ) \right]-2\left[ 1.5\sqrt{3}+6 * asin(\frac{3}{2\sqrt3} ) \right]\\ =2\left[ 6 * \frac{\pi}{2} \right]-2\left[ 1.5\sqrt{3}+6 * asin(\frac{\sqrt3}{2} ) \right]\\ =6\pi-2\left[ 1.5\sqrt{3}+6 * \frac{\pi}{3} ) \right]\\ =6\pi-2\left[ 1.5\sqrt{3}+2\pi ) \right]\\ =6\pi-3\sqrt{3}-4\pi \\ =2\pi-3\sqrt3\)
So the desired area in the middle is
\(middle \;area =36-[\pi*(2\sqrt3)^2-4*(2\pi-3\sqrt3)]\\ middle \;area =36-[12\pi-8\pi+12\sqrt3)]\\ middle \;area =36-[4\pi+12\sqrt3)]\\ middle \;area =36-12\sqrt3-4\pi \;\;cm^2\\ middle \;area \approx 2.65 cm^2\\\)