Melody

Chris, this is an art of problem solving questions, we have a loose agreement not to answer these.

Thanks Chris,      

It wasn't that much really.  Thinking it through required a bit of effort though.

I hope Willy, or any other interested person, can work through what I have said.    

I've added an amended graph that might help you a bit.

Thanks Tiggsy,

That is great.

I will take a proper look a little later.

Thanks Chris, I have fun sketching these. 

My sketch is accurate, my answer would be right within approx 2 decimal places.

My answer has as much accuracy as the Geogebra program allows. This appears to be 2 dp.

This video seems to make it more difficult than necessary but it is probably doing that on purpose.

If you get your head around difficult terminology it usually means you are learning properly, hopefully at a deeper level.

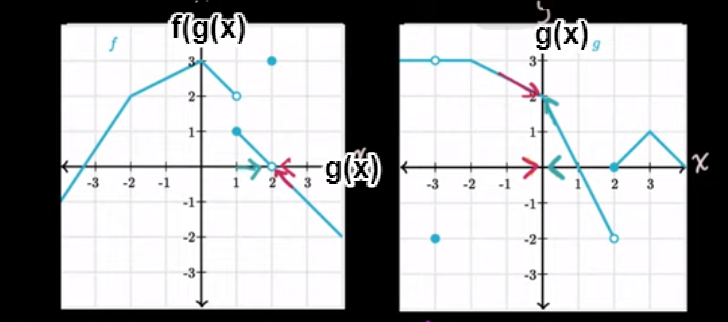
A better graph representation:

\(\displaystyle \lim _{x\rightarrow 0}\;f(g(x))\\ \text{I would just have said that } g(0)=2 \;\;so\;\;\\ =\displaystyle \lim _{x\rightarrow 0}\;f(2)\\ =0\)

Let's see what the video teacher was saying

\(\displaystyle \lim _{x\rightarrow 0}\;f(g(x))\\ \)

Look at the g graph first.

I am just referring to red stuff that he talked about.  He has not explained it well.

look at g function first     (vertical axis is g, horizontal axis is x)

As x approaches 0 from the negative x side (he has called the left side the below side.)

g approaches 2 from higher g values,... from above   

Now move over to the f function

If you are going to find f(g(x)) then the horizontal axis become   g(x) or g      NOT x  and the vertical axis is f(g(x)) or just f for short.

So g is approaching 2 from above  means that on the f graph, g is approaching 2 from the right side.  

See if you can get your head around that.

LaTex

\displaystyle \lim _{x\rightarrow 0}\;f(g(x))\\
\text{I would just have said that } g(0)=2 \;\;so\;\;\\
=\displaystyle \lim _{x\rightarrow 0}\;f(2)\\
=0

I do not understand the algebraic answers above. I mean i do not see the logic that Spring has used

\(\sqrt{12-\!\sqrt{12-\!\sqrt{12-\cdots}}} \qquad=\;\;?\\ \text{First, since the square root is in the question, the answer must be positive.}\\ let\\ y=\sqrt{12-\!\sqrt{12-\!\sqrt{12-\cdots}}} \\ then\\ y=\sqrt{12-y}\\ y^2=12-y\\ y^2+y-12=0\\ (y-3)(y+4)=0\\ y=3\;\;or \;\;-4\\ \text{y cannot be negative}\\ y=3 \)

What do these ones end with

10!

11!

12!

and all the way to the end?

So what do you need to consider.?

There are 20 cars in my building's parking lot. All of the cars are red or white. Also, all the cars are either 2-door or 4-door. 15 of them are red, 18 of them are 4-door, and 3 of them are 2-door and white. How many of the cars are 4-door and red?

Unless I am missing something the question does not make sense.

18 are  four-door which means that 2 are two-door.

So 3 cannot be 2-door and white.