A geometric series \(b_1+b_2+b_3+\cdots+b_{10}\) has a sum of 180.
Assuming that the common ratio of that series is \(\dfrac{7}{4}\),
find the sum of the series \(b_2+b_4+b_6+b_8+b_{10}\).
see: https://web2.0calc.com/questions/geometric-sequences_5
My attempt:
\(\text{Let $b_2+b_4+b_6+b_8+b_{10} = x$ } \)
\(\begin{array}{|lrcll|} \hline & b_1+b_2+b_3+b_4+b_5+b_6+b_7+b_8+b_9+b_{10} &=& 180 \\ & (b_1+ b_3+ b_5+ b_7+ b_9)+(b_2+b_4+b_6+b_8+b_{10}) &=& 180 \\ & (b_1+ b_3+ b_5+ b_7+ b_9)+x &=& 180 \\ (1) & \mathbf{ b_1+ b_3+ b_5+ b_7+ b_9} &=& \mathbf{180 -x} \\ \hline \end{array}\)
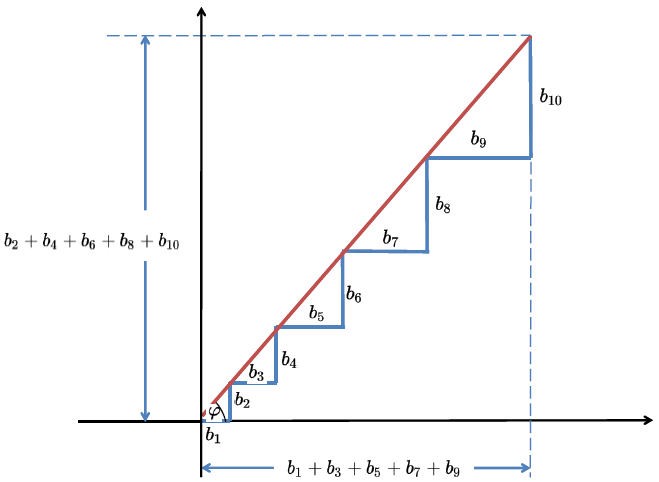
\(\begin{array}{|rcll|} \hline \text{common ratio }=\dfrac{7}{4} = \dfrac{b_2}{b_1}= \dfrac{b_6}{b_5}= \dfrac{b_8}{b_7}=\dfrac{b_{10}}{b_9}=\tan(\varphi) \quad | \quad =\text{ slope of the red line} \\ \hline \end{array}\)
\(\begin{array}{|lrcll|} \hline &\text{slope of the red line} = \text{common ratio} = \dfrac{7}{4} &=& \dfrac{b_2+b_4+b_6+b_8+b_{10}}{b_1+ b_3+ b_5+ b_7+ b_9} \\ & \dfrac{7}{4} &=& \dfrac{x}{b_1+ b_3+ b_5+ b_7+ b_9} \\ (2)& \mathbf{b_1+ b_3+ b_5+ b_7+ b_9} &=& \mathbf{\dfrac{4}{7}x} \\ \hline \end{array} \)
\(\begin{array}{|lrcll|} \hline (1) & \mathbf{ b_1+ b_3+ b_5+ b_7+ b_9} &=& \mathbf{180 -x} \\ (2)& \mathbf{b_1+ b_3+ b_5+ b_7+ b_9} &=& \mathbf{\dfrac{4}{7}x} \\ \hline & 180 -x &=& \dfrac{4}{7}x \quad | \quad \cdot 7 \\ & 7\cdot 180 -7x &=& 4x \\ & 11x &=& 7\cdot 180 \\\\ & x &=& \dfrac{7\cdot 180}{11} \\ \\ & \mathbf{x} &=& \mathbf{ \dfrac{1260}{11} } \\ \hline \end{array} \)
The sum of the series \(b_2+b_4+b_6+b_8+b_{10} = \mathbf{ \dfrac{1260}{11} }\).
![]()