Let b and c be constants such that the quadratic -2x^2 + bx + c
has roots and 3 + sqrt(13) and 3 - sqrt(13).
Find the vertex of the graph of the equation y = -2x^2 + bx + c.
This is a concave down parabola
The axis of symmetry is obviously x=3 because this is a halfway between the two roots.
\(-2x^2 + bx + c=0\\ \text{The roots of any quadraic are given by}\\ x=\frac{-b}{2a}\pm\frac{\sqrt{b^2-4ac}}{2a}\\ so\\ x=\frac{-b}{-4}\pm\frac{\sqrt{b^2+8c}}{-4}\\ x=\frac{b}{4}\pm\frac{\sqrt{b^2+8c}}{-4}\\ \frac{b}{4}=3\qquad so \qquad b=12\\ x=3\pm\frac{\sqrt{144+8c}}{-4}\\ \frac{\sqrt{144+8c}}{-4}=\sqrt{13}\\ \frac{144+8c}{16}=13\\ \frac{144+8c}{16}=13\\ 8c=64\\ c=8\\~\\ \text{So the quadratic is }-2x^2 + 12x + 8\\ f(x)=-2x^2 + 12x + 8\\ f(3)=26 \)
Here is the graph that I used as a check
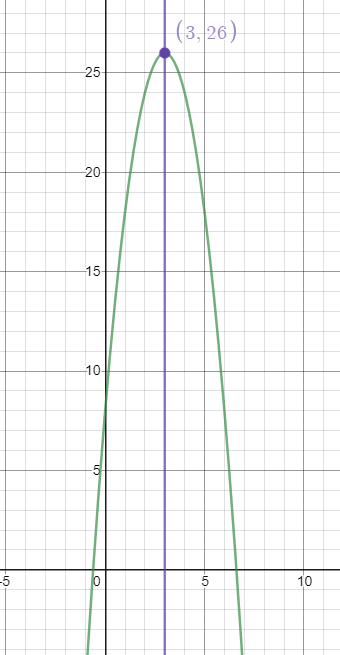
LaTex
-2x^2 + bx + c=0\\
\text{The roots of any quadraic are given by}\\
x=\frac{-b}{2a}\pm\frac{\sqrt{b^2-4ac}}{2a}\\
so\\
x=\frac{-b}{-4}\pm\frac{\sqrt{b^2+8c}}{-4}\\
x=\frac{b}{4}\pm\frac{\sqrt{b^2+8c}}{-4}\\
\frac{b}{4}=3\qquad so \qquad b=12\\
x=3\pm\frac{\sqrt{144+8c}}{-4}\\
\frac{\sqrt{144+8c}}{-4}=\sqrt{13}\\
\frac{144+8c}{16}=13\\
\frac{144+8c}{16}=13\\
8c=64\\
c=8\\~\\
\text{So the quadratic is }-2x^2 + 12x + 8\\
f(x)=-2x^2 + 12x + 8\\
f(3)=26