I might as well post my solution.
We can use a very handy formula, which is very important to remember, \(A=rs\), where \(A\) is the area of the figure, \(r\) is the inradius when it is a complete circle, and \(s\), the semi-perimeter of the figure, or you can call it as, "half the perimeter."
Now, this is where the tricky part comes in. we can reflect the second part of the figure, like this:
After drawing this figure, we can find the area of one triangle, the multiply it by two, to find the area of the rhombus. 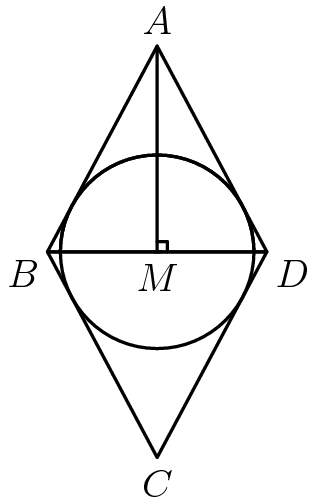 Drawing the altitude of sixteen to the base, we find that the area is \(\frac{1}{2}*16*15=120\). Multiply it by two since there are two triangles, to get \(2*120=240.\)And, using the Pythagorean Theorem, that gives us \(\sqrt{8^2+15^2}=\sqrt{17^2}=17.\) Multiply it by four to find the whole(full) perimeter, and divide it by two to find the semi-perimeter, to get \(17*2=34.\) Now, we found \(A\) and \(s\), and we divide it to get \(r\), to get \(\frac{240}{34}=\boxed{\frac{120}{17}}.\)
Drawing the altitude of sixteen to the base, we find that the area is \(\frac{1}{2}*16*15=120\). Multiply it by two since there are two triangles, to get \(2*120=240.\)And, using the Pythagorean Theorem, that gives us \(\sqrt{8^2+15^2}=\sqrt{17^2}=17.\) Multiply it by four to find the whole(full) perimeter, and divide it by two to find the semi-perimeter, to get \(17*2=34.\) Now, we found \(A\) and \(s\), and we divide it to get \(r\), to get \(\frac{240}{34}=\boxed{\frac{120}{17}}.\)
.