All Answers 356458 Answers

-3-21 = -24

Thanks very much Alan     

Yes, they're the same.  Your method is very neat!

This question has been asked hundreds of times.

I just googled it and got more than 2000 results just from this website!

This is my most recent decent answer.

Here is the logic behind it.

Just use Pythagoras's theorem to solve it.

Thanks Alan,

I also got 343 but i think my method was a bit unconventional and I wan't sure about the power of 6 bit.

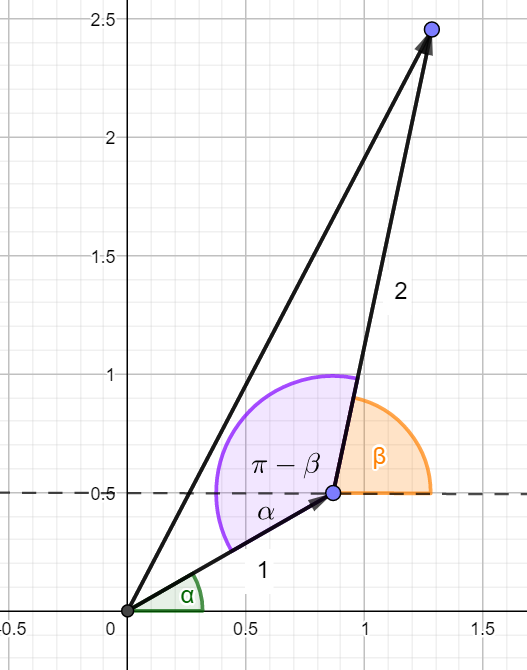
This is how I did it.

(the angles in the pic  are not to scale)   

\(\beta = \frac{10\pi}{21},\qquad \alpha = \frac{\pi}{7}\)

To find the length of the resultant vector I used the cosine rule.

\(length^2=1^2+2^2-2*1*2*cos(\pi-\beta +\alpha)\\ length^2=5-4cos(\pi-(\beta -\alpha))\\ length^2=5+4cos(\beta -\alpha)\\ length^2=5+4cos(\frac{10\pi}{21} -\frac{3\pi}{21})\\ length^2=5+4cos(\frac{\pi}{3})\\ length^2=5+4cos(\frac{\pi}{3})\\ length^2=5+2\\ length^2=7\\ length^6=343\\ \text{So I think this means that } |(z+w)|^6=343\\ ~\\ \text{But I am asked for }|(z+w)^6| \\  \text{Alan gave the same answer, are they always the same??}\\\)

Could you comment please Alan?

LaTex:

length^2=1^2+2^2-2*1*2*cos(\pi-\beta +\alpha)\\
length^2=5-4cos(\pi-(\beta -\alpha))\\
length^2=5+4cos(\beta -\alpha)\\
length^2=5+4cos(\frac{10\pi}{21} -\frac{3\pi}{21})\\
length^2=5+4cos(\frac{\pi}{3})\\
length^2=5+4cos(\frac{\pi}{3})\\
length^2=5+2\\
length^2=7\\
length^6=343\\
\text{So I think this means that } |(z+w)|^6=343\\
~\\
\text{But I am asked for }|(z+w)^6| \\
 \text{Alan gave the same answer, are they always the same??}\\

I have seen this question, or very similar ones, very recently.

I assume this is a partial fraction question as interpreted by Guest#1.  Guest#1 has the right approach, but unfortunately mistakenly set a - 2b = -7, where it should be a - 2b = 7.  Given this correction you shoud be able to determine a and b.

The following works, but is a little tedious:

\(\frac{(x+7)}{(x²-x-2)}+\frac{a}{x-2}+\frac{b}{(x+1)}\)

Such that what?  Is there meant to be an equal sign somewhere?

I used sine rule followed by trig identities to get the value of sin

Then I used cosine rule to find the answer.

It was not an easy question.

I did not check my working but I also got an approx answer of 35.001.

Factor n^3 - n to get n(n^2 - 1) then n(n - 1)(n + 1) using the diference of two squares.  Hence the largest integer that divides n^3 - n is n + 1.

Just do it on a calculator.

Well now you will know how to do it.      

Thanks for the answer guest.  

I would like to see too.

For each number from 1 to 99, Andrew wrote down the sum of its digits. What is the mean of the numbers Andrew wrote down?

Hello Guest!

\(\sum_{k=1}^n\ k=\frac{n^2+n}{2}\)

\(\sum_{k=1}^9\ k=\frac{9^2+9}{2}=45\)

The mean of the numbers from 1 to 99 is

\(\frac{10\cdot 45+9\cdot 45}{90+99}=\frac{855}{189}=\color{blue}4.\overline{523809}\)

  !

Maybe it would be in your interest to present your questions better.

All those unnecessary dollar signs make it difficult to read and I feel that if you cannot be bothered to present your question properly then it is not worth my effort to attempt to answer.  

thank you so much, but could you show me how you got the answer, rather than just the solution?

Hint:

From any arc of a circle, the angle subtended to the centre is twice that subtended to the circumference.

In this instance, the arc is minor arc BD

you can take if from there.

thanks, i kept thinking that they wanted me to multiply the entire thing by -3x and kept getting d as my answer

By power of a point, the radius of the circle is 4*sqrt(7).

By the cosine law, b = 35.