All Answers 358098 Answers

M + T = 36,   

M/2 + 2T =42, solve for M, T

M = 20 pounds - what Mary has

T = 16 pounds - what Tom has.

I think all you need to do is to find their LCM:

LCM[1, 2, 3, 4, 5, 6, 7] =420 days - when ALL 7 can dine together.

The slope   of   Ax + By  =  3   is      -A/B    

And  x + 3y  = - 5  ⇒  3y  =  -x  - 5     divide through by 3  ⇒  y = (-1/3) - 5/3

So....the slope of the second line =  (-1/3)   

And since this is parallel to the first line,  this implies that

-1/3  = -A/B

So  A = 1   and  B    = 3

Then B - A  =   3  -  1   =   2

Hmmm...you answer sounds much better than mine!  (Especially the tapestry, lol!)

As follows:

could you give a full explanation for your answer??

Hi Macabrasubwoofer!

I think the answer to the first question is A, strong negative because we see a correlation of downwards sloping.

I also believe that the answer to the second question is D, no correlation. This is because they do not follow any sort of support/line, rather, they are all scattered. 

Hope this helped!

Noori

(105, 114, 123, 132, 141, 150, 204, 213, 222, 231, 240, 303, 312, 321, 330, 402, 411, 420, 501, 510, 600, 1005, 1014, 1023, 1032, 1041, 1050, 1104, 1113, 1122, 1131, 1140, 1203, 1212, 1221, 1230)>>Total =36 in 12 hours.

Yes, that is correct. Thank you so much!!

(you should create an account so that when you answer questions you can get points) 

Q = (0,3) and K = 16.

The equation of the line is y = -4x + 7.

Tulip =20

Pansy=5

sunflower*sunflower= 2 (I guess)     I am not sure what (sunflower sunflower) means 

sunflower= sqrt2

sunflower+tulip*Pansy = sqrt2+100

Or maybe you just get a crazy tapestry.

OK young person! Here is a computer code that I wrote in Python 3 to count ALL 10-digit numbers whose SUM is divisible by 2!!

%%time
# Efficient Python 3 program to sum up the # 
# multiples of digit n in a range of 2 - 10-digit integers #
# E.G. "What is the total  number and sum of all 3-digit integers that are
#  mutiples of 7, or are divisible by 7?". Answer =70,336 #
  
# find the Sum of having n digit  
# and divisible by the number 
def totalSumDivisibleByNum(digit, number): 
  
    # compute the first and last term 
    firstnum = pow(10, digit - 1) 
    lastnum = pow(10, digit) 
  
    # first number which is divisible 
    # by given number 
    firstnum = (firstnum - firstnum % number)+number
    
    # last number which is divisible 
    # by given number 
    lastnum = (lastnum - lastnum % number ) 
    
    # total divisible number 
    count =int ((lastnum - firstnum) / number+1  ) 
    print("Total count =", f"{count:,d}")
    # return the total sum 
    return int(((lastnum + firstnum) * count) / 2) 
  
  
# Driver code 
digit =10 ; num = 2

print("Total Sum =", f"{totalSumDivisibleByNum(digit, num):,d}") 
  
Total count = 4,500,000,000
Total Sum = 24,750,000,004,500,000,000
Wall time: 0 ns

A class of 30 students recently took a test. If 20 students scored 80, 8 students scored 90, and 2 students scored 100, then what was the class average (the mean) on this test?  

Add up all the scores then divide that total by the number of students.  

  20 students made   80 so the total of those 20 is                       20 • 80   =  1600  

    8 students made   90 so the total of those   8 is                         8 • 90   =    720   

    2 students made 100 so the total of those   2 is                         2 • 100  =   200  

Add up all the scores                                                     1600 + 720 + 200  =  2520  

Divide that by 30                                                                           2520/30  =    84  is their average    

_.

Use AP formula to sum them up:

Sum = 15/2 * [2*20 + 4*14 ]

Sum = 7.5 * [40   +     56 ]

Sum = 7.5 *      96

Sum = 720 chairs in the theater.

Continued here

Maybe someone else would like to continue from where I have left off ?

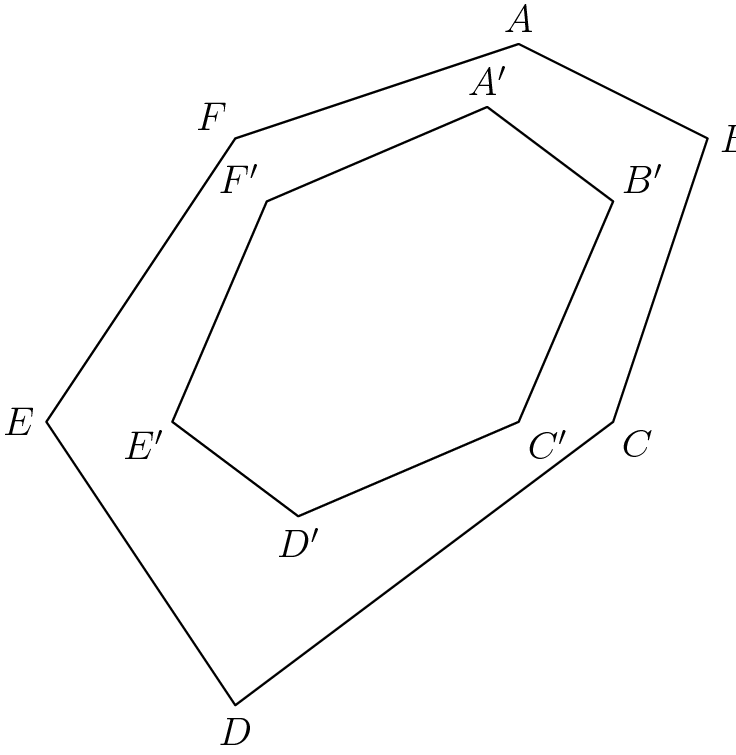
Let ABCDEF be a convex hexagon. Let A', B', C', D', E', F' be the centroids of triangles FAB, ABC, BCD, CDE, DEF, EFA, respectively. (a) Show that every pair of opposite sides in hexagon A'B'C'D'E'F' (namely A'B' and D'E', B'C' and E'F', and C'D' and F'A') are parallel and equal in length. (b) Show that triangles A'C'E' and B'D'F' have equal areas.

Hi Gwen,

I have spent time playing with this question. 

Graphically I have convinced myself that it is true.

I tried to follow Gavin's logic in the other answer but he seemed to jump a big step. Maybe what he was saying would have been more obvious if his pic had still been visible, but I doubt it.

However I did simply the problem to look only at one half of hexagon, which is a quadrilateral.  The properties of each quadrilateral will be the same so if you can prove 

1)     B'C' is parallel to AD   and that     (that is what it always appears to be from my diagram.)

2)       B'C' = one third of AD                  (also what it always appears to be from my diagram.)

then, by extension, you can prove what you are being asked.

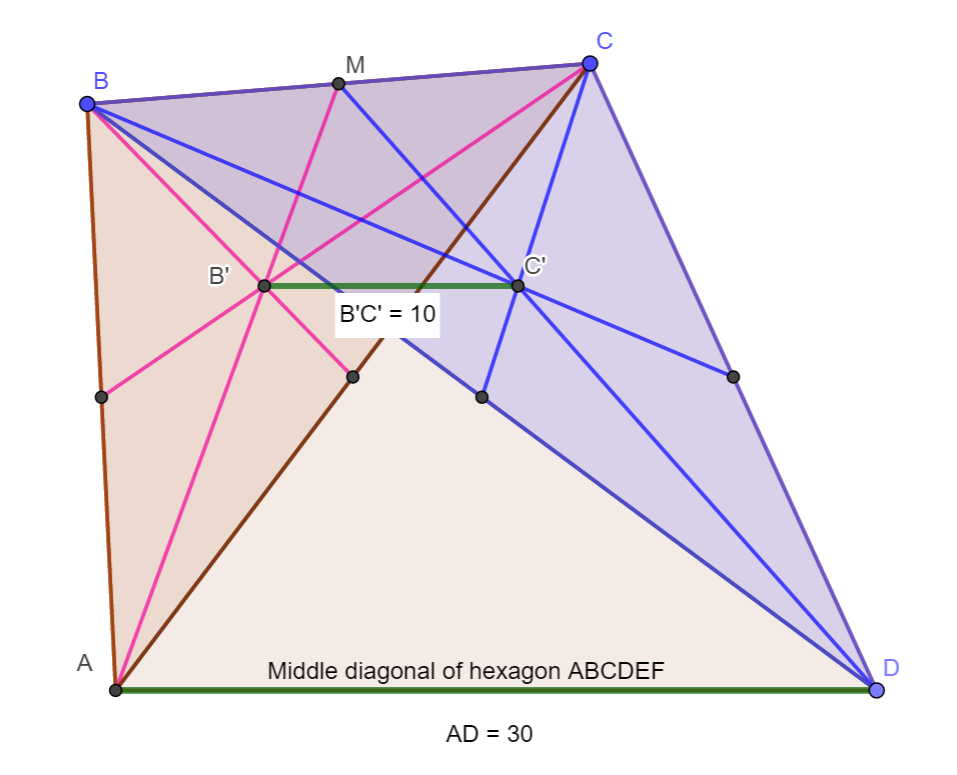
Here is the interactive diagram that you can play with.

Only point A is fixed, the rest of the diagram can be dragged wherever you want. The stated requirements will stay correct.

Are you ok. with vectors ?

I can show you a fairly simple vector algebra solution, (to both parts).

What is an equation of the line that passes through the point (-6, -7) and is perpendicular to the line 6x + 5y = 30?