All Answers 357329 Answers

Lots of posters on this forum do.    Do you have a question?

4/5 b - 9 = 3     add 9 to both sides

4/5 b = 12        Multiply both sides by 5

4 b = 60           divide both sides by 4

b=15

Since you wanted another mathematician to check this, I will say that this is how I interpreted the question as well. I believe you got the correct answer, Melody. 

s to d on calculator

Ok- so the information given is that we have to take a 7 block path, no cutting across blocks.

we would have to take 4 steps to the right and 3 up in any order

therefore 

$(7/3) {7X6X5 \over 3X2X1}= 35$

I think the best thing to do here is to construct a diagram. The problem gives you vertices with coordinates from the Cartesian plane, and it even gives you an inequality. Here is the construction I created. I will reference it throughout the solving process:

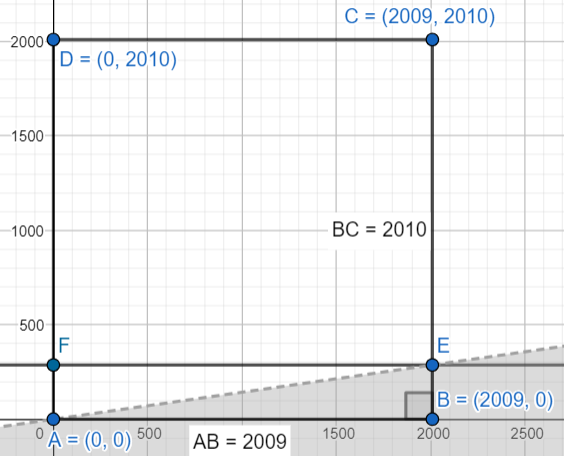
I first located the given coordinates and connected them with vertical and horizontal lines. I then graphed the inequality$x>7y$, which can be rewritten as $y<\frac{x}{7}$ . I added a few points, as they will become relevant when I solve.

One way to solve this problem is to figure out the ratio of the area created by the inequality $y<\frac{x}{7}$ and the sides of the rectangle to the area of the entire rectangle. I will do this by first finding the coordinates of the point E. Point E is located on $\overline{BC}$ , so its x-coordinate is also 2009. If you know the x-coordinate, then the y-coordinate of any point on $y=\frac{x}{7}$ is $\frac{x}{7}$ . Therefore, the y-coordinate is $\frac{2009}{7}$ . 

The formula for the area of the triangle is $\frac{1}{2}bh$ . $\triangle ABE$ is a right triangle, so the base and height are the side lengths that are not the hypotenuse. We know the length of the base, $AB$ , because it is in the diagram. The height is the length of $BE$ , or $\frac{2009}{7}$

$A_{\triangle}=\frac{1}{2}*AB*BE=\frac{1}{2}*2009*\frac{2009}{7}=\frac{2009^2}{14}$

We can also calculate the area of the rectangle

$A_{\text{rect.}}=bh=AB*BC=2009*2010$

As aforementioned, the probability of (x,y) such that x>7y is just the ratio of these areas.

If there is an ordinary six-sided die and you are painting two sides with the same color, then you can calculate the number of ways this can occur.

• There are six choices for the first face.
• There are five choices for the second face.

Therefore, the total number of choices is equal to $6*5$ or 30. However, the order in which each face is colored is really immaterial in this problem; for example, if I paint the side 4 and then side 1, then it is the same as painting side 1 and then 4. Because of this, I must divide by the number of combinations of duplicates, 2, in this case. 

Therefore, there are $\frac{6*5}{2}=3*5=15 \text{ combinations}$ . 

We still are not done. We need to determine which combinations result in the product of a 6.  Painting 1 and 6 or 2 and 3 would result in a product of 6. This means there are two combinations that do not meet the original condition. 

$15-2=13\text{ combinations}$

Here's my solution:

In this currency system, known as the pound sterling, there are 8 denominations of coins. They are:

• 1p
• 2p
• 5p
• 10p
• 20p
• 50p
• £1
• £2

These are the building blocks of the British currency. I can use six coins by having £1+50p+20p+5p+2p+1p

Hey, Guest!

Notice that adding a set of parentheses will solve this issue. The calculator will evaluate 50+(10%) as 50.1

Correct.  I forgot about b having to be less than or equal to 1 at the end!

f(x)=x^3

f(2)+f(-2)=2^3+(-2)^3 = 8+-8 = 0

$\left(\dfrac 1 4 \right)^4 = \dfrac{1}{256}$

The electronic configuration of $Re^{7+}$ is$[Xe]$ $5d^0$ $6s^0$ and there is no unpaired electron in the outer shell to contribute in heat capacity.

I just realized. This question has also been answered b4. Just another thing to keep in mind. Hehe. 

Okay. I'm gonna attempt to explain how it works. 

The second and fourth rows of the pascal's triangle have only even digits (excluding the 1s).

If we look further down into Pascal's triangle, we can see that rows 8 and 16 are the next two rows with only even digits (excluding the 1).

Do you notice a pattern here?

The even digit rows in order are: $2, 4, 8, 16...$

The number of each subsequent row is twice the number of each preceding row.

Using this knowledge, we can find that the rows with only even numbers, less than 100 are:

$2, 4, 8, 16, 32, 64$, which would give us an answer of $\boxed 6$ rows.

(P.S. When you are learning about Pasal's triangle, stuff like this is good to keep in mind)

I think questions like this one are always really hard to understand and I would like another mathematician to check my answer.

Use my pic, which is near enough to the same.

Think about a horizontal line through the graph.  

At the top it will pass through the graph twice so  g(c)=2

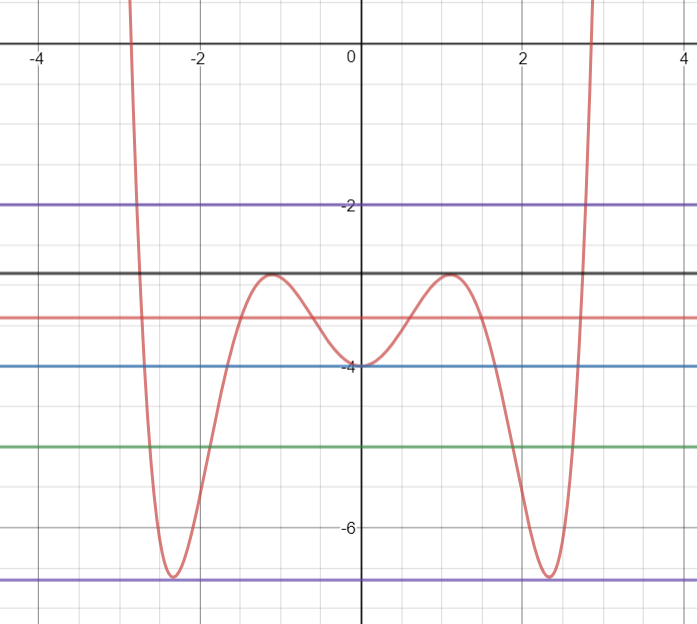
Here is a pic

I have drawn six horizonal lines.

For the top (purple - 1st ) one    f(x)=-2

this crosses the graph f(x) at 2 different x values so  g(-2)=2

the next horizontal line (black 2nd )  palsses through 4 points so  g(-2.8)=4

the 3rd horizontal line (red )  palsses through 6 points so  g(-3.4)=6

the 4th horizontal line (blue )  palsses through 5 points so  g(-4)=5

the 5th horizontal line (green)  palsses through 4 points so  g(-5)=4

the bottom horizontal line (purple )  palsses through 2 points so  g(-6.7)=2

So g(c) can be 2, 4, 5, or 6       

The average of the distict values of g(c) = (2+4+5+6)/4 = 17/4 = 4.25

I am pretty sure that is correct.

Not sure....

10% 0f 50 is

 10/100 * 50 =  5

So 50 + 10% ===== 50 +5 = 55    Done....no other answer...

I would do it the same way as shown on this video.

got it!

Don't worry about it this time unless someone asks for it. 

Just don't do it again :)

Every now again I wll spend a long time answering a question and then when I go to post it the question has been removed, or changed without comment. It can be infuriating.

oh sorry!! do i post the question again ?

Please do not delete your questions.

Someone could have been in the process of answering it.

Plus someone else could have learned from that answer.

If you do not need an answer anymore just write a new post saying something like:

"Thanks to all those that look at my question but I do not need an answer any more.

I have worked it our for myself   "