tertre

1. We can use the handshakes formula here...n(n-1) / 2 =21 n(n-1)=42, n=7 people at the party.

2. Think of arranging three identical letters with five other identical letters. How many ways are there to do this?

We can also use modular arithmetic here.

The goal here...is to write the expression as a sum of squares plus a number.

Try this, and see what you get.

(x,y)=(2,-3)

Plug the values into the expression, and get -1?

See here: https://web2.0calc.com/questions/what-is-0-48-expressed-as-a-fraction-in-simplest_1#r3​

There are a 100 integers between 1-100, inclusive. Since 50 is \(2*5^2\), it has \((1+1)(1+2)=(2)(3)=6\) factors. Thus, the answer is \(\frac{6}{100}=\boxed{\frac{3}{50}}. \)

We have to find a multiple of 9, that when divided by 25 leaves a remainder of 1.

Therefore, 126 is congruent to 1(mod25)...so x = 126 / 9 = 14.

Thus, 14+11=25 and dividing this result by 25 leaves a remainder of 0.

-tertre

Hint: They all have the same slope.

Non-Trig Solution:

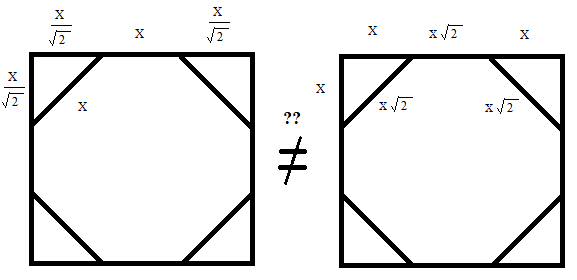
Draw an octagon...like the diagram as shown below. Since the perimeter of the octagon is 32 cm, each of its side length are  32 / 8 = 4 centimeters.

Now, draw a square around it...forming four 45-45-90 degree triangles. The side length opposite to the 45 degree angles is \(x\sqrt{2}=4, x=\frac{4}{\sqrt{2}}=2\sqrt{2}\).

Find the area of each triangle, and multiply that by 4, yielding...\(4*4=16.\)

The area of the square on the other hand is \((4\sqrt{2}+4)^2=48+32\sqrt{2}.\)

Finally, (the area of the square) - (area of the four triangles = (area of the octagon).

Thus, we have \(48+32\sqrt{2}-16=\boxed{32+32\sqrt{2}}.\)

Let's see Melody...

We have \(4.\overline{8}=10*.4\overline{8}\).

\(4.\overline{8}\) can be rewritten as \(4 \frac{8}{9}\), or \(\frac{44}{9}.\)

Then, we have \(\frac{44}{9}*\frac{1}{10}=\frac{22}{45}.\)

Yes, that is right...

We have \(\frac{pq}{2}\), as \(p\) and \(q\) are the two diagonals. Thus, we have \(\frac{40*q}{2}=840\), and \(40q=1680, q=42.\)

Now, we have four right triangles by drawing the two diagonals. If you see closer, we can use the Pythagorean Theorem, to find the side length, which is \(\sqrt{20^2+21^2}=\boxed{29}.\)