All Answers 356371 Answers

i tried that... its incorrect :(

Out of four ways, there is only one way to set up the chords A_1 A_2 and A_3 A_4 so that they intersect, so the probability is 1/4.

Here: https://web2.0calc.com/questions/help_88352

You can track the probabilities using different case, i.e. Anty gets to 0 after 1 steps, 2 steps, 3 steps, and so on.  This gives us e_1 = 1/2*1 + 1/4*2 + 1/8*3 + 1/16*4 + ... By arithmetico-geometric series, e_1 = 2.  Similarly, e_2 = 1/2*2 + 1/4*3 + 1/8*4 + 1/16*5 + ... = 3, so (e_1,e_2) = (2,3).

The ratio of 12 to the area of the big triangle is 1/6, so the probabiity is 1/6.

[3.1 x 10^6  -  7.2 x 10^4] =3,028,000 - increase in cells

5x - 7y = -34................(1)
4x - 7y = -30................(2)

Subtract equation (2) from equation (1)
x = - 4. Sub x into equation (1)
5*-4 - 7y = -34
-20 - 7y  = -34
-7y =-34 + 20
-7y = - 14        Divide both sides by -7
y = 2  and x = - 4

629 = 17 * 37

a=17  and  b=37

"Let triangle ABC be equilateral, where the side length is 3. A point D is chosen at random inside the triangle. What is the probability that the length AD is at most 1?"

"Team A are playing against Team B in a baseball tournament. The first team to win three games wins the tournament. Team A have a probability of 2/3 of winning each game. Find the probability that they win the tournament."

Thanks Omi, your answer is of course correct :)

Four points \(A_1,\ A_2,\ A_3,\ \)and \(A_4\) are chosen at random on a circle.
Find the probability that chords \(\overline{A_1 A_2}\) and \(\overline{A_3 A_4}\) intersect.

My attempt:

\(\begin{array}{|r|cl|} \hline & & \text{intersect} \\ \hline & 2~3 \\ 1 & 1~~~4 \\ \hline & 2~4 \\ 2 & 1~~~3 \\ \hline & 3~2 \\ 3 & 1~~~4& \checkmark\\ \hline & 3~4 \\ 4 & 1~~~2 \\ \hline & 4~2 \\ 5 & 1~~~3 & \checkmark\\ \hline & 4~3 \\ 6 & 1~~~2 \\ \hline & 1~3 \\ 7 & 2~~~4 \\ \hline & 1~4 \\ 8 & 2~~~3 \\ \hline & 3~1 \\ 9 & 2~~~4 & \checkmark\\ \hline & 3~4 \\ 10 & 2~~~1 \\ \hline & 4~1 \\ 11 & 2~~~3& \checkmark\\ \hline & 4~3 \\ 12 & 2~~~1 \\ \hline & 1~2 \\ 13 & 3~~~4 \\ \hline & 1~4 \\ 14 & 3~~~2 & \checkmark\\ \hline & 2~1 \\ 15 & 3~~~4 \\ \hline & 2~4 \\ 16 & 3~~~1 & \checkmark\\ \hline & 4~1 \\ 17 & 3~~~2 \\ \hline & 4~2 \\ 18 & 3~~~1 \\ \hline & 1~2 \\ 19 & 4~~~3 \\ \hline & 1~3 \\ 20 & 4~~~2 & \checkmark\\ \hline & 2~1 \\ 21 & 4~~~3 \\ \hline & 2~3 \\ 22 & 4~~~1 & \checkmark\\ \hline & 3~1 \\ 23 & 4~~~2 \\ \hline & 3~2 \\ 24 & 4~~~1 \\ \hline \end{array}\)

The probability is \(\dfrac{8}{24} = \mathbf{\dfrac{1}{3}}\)

During a donation drive, Jaheem donated as much as 3/7 of the amount that Cason donated. Li Wei donated $49 more than Jaheem. How much did Cason donate if they donated $660 altogether?

​geometry proof

\(\begin{array}{|rcll|} \hline \mathbf{\text{In ACP sin-rule:}} \\ \hline \frac{w}{\sin(90^\circ-\alpha)} &=& \frac{CP}{\sin(45^\circ)} \quad (1) \\ \hline \end{array} \begin{array}{|rcll|} \hline \mathbf{\text{In CPQ sin-rule:}} \\ \hline \frac{\sin(45^\circ)}{v} &=& \frac{\sin(\alpha)}{CP} \quad (2) \\ \hline \end{array} \\ \begin{array}{|lrcll|} \hline (1)\times(2): & \frac{w}{\sin(90^\circ-\alpha)}\times \frac{\sin(45^\circ)}{v} &=&\frac{CP}{\sin(45^\circ)} \times \frac{\sin(\alpha)}{CP} \\\\ & \frac{w}{\cos(\alpha)}\times \frac{\sin(45^\circ)}{v} &=&\frac{\sin(\alpha)}{\sin(45^\circ)} \\\\ & \frac{w}{v} &=& \frac{\sin(\alpha)\sin(\alpha)} {\sin^2(45^\circ)} \\\\ & \frac{w}{v} &=& \frac{2\sin(\alpha)\sin(\alpha)} {2\sin^2(45^\circ)} \\ & && \boxed{\sin(45^\circ) = \frac{\sqrt{2}}{2} \\ \sin^2(45^\circ) = \frac{1}{2} }\\ & \frac{w}{v} &=& \frac{2\sin(\alpha)\sin(\alpha)} {2*\frac{1}{2}} \\ & \frac{w}{v} &=& 2\sin(\alpha)\sin(\alpha) \\ & && \boxed{ 2\sin(\alpha)\sin(\alpha)= \sin(2\alpha) }\\ & \mathbf{\frac{w}{v}} &=& \mathbf{\sin(2\alpha)} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \mathbf{\text{In BCQ sin-rule:}} \\ \hline \frac{u}{\sin(\alpha-45^\circ)} &=& \frac{CQ}{\sin(45^\circ)} \quad (3) \\ \hline \end{array} \begin{array}{|rcll|} \hline \mathbf{\text{In CPQ sin-rule:}} \\ \hline \frac{\sin(45^\circ)}{v} &=& \frac{\sin(135^\circ-\alpha)}{CQ} \quad (4) \\ \hline \end{array} \\ \begin{array}{|lrcll|} \hline (3)\times(4): & \frac{u}{\sin(\alpha-45^\circ)}\times \frac{\sin(45^\circ)}{v} &=&\frac{CQ}{\sin(45^\circ)} \times \frac{\sin(135^\circ-\alpha)}{CQ} \\\\ & \frac{u}{\sin(\alpha-45^\circ)}\times \frac{\sin(45^\circ)}{v} &=&\frac{\sin(135^\circ-\alpha)}{\sin(45^\circ)} \\\\ & \frac{u}{v} &=& \frac{\sin(\alpha-45^\circ)\sin(135^\circ-\alpha)} {\sin^2(45^\circ)} \\ & && \boxed{\sin(45^\circ) = \frac{\sqrt{2}}{2} \\ \sin^2(45^\circ) = \frac{1}{2} }\\ & \frac{u}{v} &=& \frac{\sin(\alpha-45^\circ)\sin(135^\circ-\alpha)} {\frac{1}{2}} \\\\ & \frac{u}{v} &=& 2\sin(\alpha-45^\circ)\sin(135^\circ-\alpha) \\ & && \boxed{\sin(135^\circ-\alpha) = \sin \Big(180^\circ-(135^\circ-\alpha) \Big)\\ = \sin(\alpha+45^\circ) }\\ & \frac{u}{v} &=& 2\sin(\alpha-45^\circ)\sin(\alpha+45^\circ) \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline && \mathbf{ \sin(\alpha-45^\circ)\sin(\alpha+45^\circ) } \\ &=&\Big(\sin(\alpha)\cos(45^\circ)-\cos(\alpha)\sin(45^\circ)\Big) \Big(\sin(\alpha)\cos(45^\circ)+\cos(\alpha)\sin(45^\circ)\Big) \\ && \boxed{ \cos(45^\circ)=\sin(45^\circ)=\frac{\sqrt{2}}{2} } \\ &=&\frac{\sqrt{2}}{2}\Big(\sin(\alpha)-\cos(\alpha)\Big) \frac{\sqrt{2}}{2}\Big(\sin(\alpha)+\cos(\alpha)\Big) \\ &=&\frac{1}{2}\Big(\sin(\alpha)-\cos(\alpha)\Big)\Big(\sin(\alpha)+\cos(\alpha)\Big) \\ &=&\frac{1}{2}\Big(\sin^2(\alpha)-\cos^2(\alpha)\Big) \\ &=&-\frac{1}{2}\Big(\cos^2(\alpha)-\sin^2(\alpha)\Big) \\ && \boxed{ \cos^2(\alpha)-\sin^2(\alpha)= \cos(2\alpha)} \\ &=&\mathbf{-\frac{1}{2}\cos(2\alpha)} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \frac{u}{v} &=& 2\sin(\alpha-45^\circ)\sin(\alpha+45^\circ) \\ \frac{u}{v} &=& 2\left(-\frac{1}{2}\cos(2\alpha)\right) \\ \mathbf{\frac{u}{v}} &=& \mathbf{-\cos(2\alpha)} \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline \mathbf{\frac{w}{v}} = \mathbf{\sin(2\alpha)} &\qquad & \mathbf{\frac{u}{v}} = \mathbf{-\cos(2\alpha)} \\\\ \left( \frac{w}{v} \right)^2 + \left( \frac{u}{v} \right)^2 &=& \Big( \sin(2\alpha)\Big)^2 + \Big(-\cos(2\alpha)\Big)^2 \\ \left( \frac{w}{v} \right)^2 + \left( \frac{u}{v} \right)^2 &=& \sin^2(2\alpha) + \cos^2(2\alpha) \\ \frac{w^2}{v^2} + \frac{u^2}{v^2} &=& 1 \quad | \quad \times v^2 \\ \mathbf{w^2 + u^2} &=& \mathbf{v^2} \\ \hline \end{array}\)

See my answer at: https://web2.0calc.com/questions/help_88352#r3 

1st angle = 60

2nd .......= 20

3rd........= 100 

"Anty the ant is on the real number line, and Anty's goal is to get to 0. If Anty is at 1, then on the next step, Anty moves to either 0 or 2 with equal probability. If Anty is at 2, then on the next step, Anty always moves to 1. Let e1 be expected number of steps Anty takes to get to 0, given that Anty starts at the point 1. Similarly, let e2 be expected number of steps Anty takes to get to 0, given that Anty starts at the point 2. "

How? Your answer doesn't make sense.

A stick is 5 units long. It is broken at two points, chosen at random. What is the probability that all three pieces are longer than 1 unit?

I will do this with a probability contour map.

Let the 3 pieces be x, y and 5 - (x+y) units long.

so

\(1) \;0 x+y\;\;  and\;\;  x+y>0\\ 5-x>y  \;\;  and\;\;  y>-x\\\)

3)  \( y<-x+5\;\;  \cap \;\; y>-x\)

 I will graph these and it will represent the sample space.

Area of sample space = 0.5*5*5 = 12.5units squared.

Now for the desired area.

What is the probability that all three pieces are longer than 1 unit?
\(x>1, \;\; y>1\\ and\\ 5-(x+y)>1\\ 4>y+x\\ 4-x>y\\ y<-x+4\\ \)

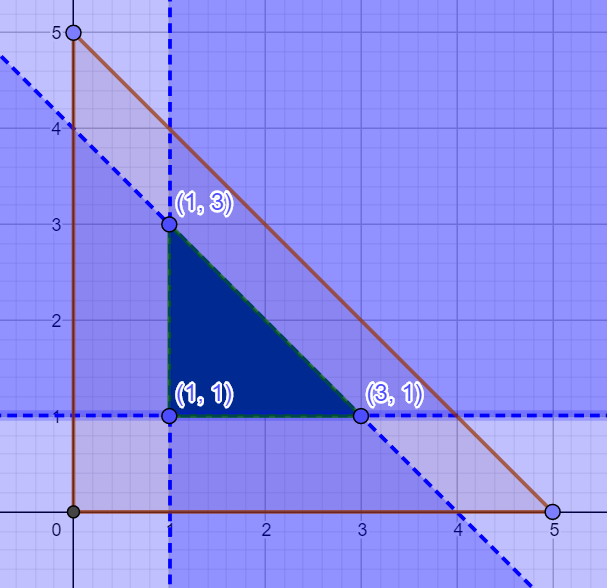
Area of middle triangle (desired outcome) = 2units squared

What is the probability that all three pieces are longer than 1 unit  =  \(\frac{2}{12.5}=16\%\)

I'm assuming that the area  of the triangle   is    (75/4) * sqrt (3)

We can solve for the side length, S,  of the triangle as follows

(75/ 4)sqrt (3)  =  (1/2) S^2  sin (60°)

(75/4)sqrt (3)  = (1/2) S^2 * sqrt (3) / 2

(75/4)  = (1/4)S^2

75  = S^2

sqrt (75)  = S

And  using the Law of Cosines we can find the  radius, R, of the  circle

75 =  2R^2  - 2R^2  cos (120°)

75 = 2R^2  + R^2

75  = 3 R^2

25 = R^2

5  = R

And the side of the square is twice  this  =  10

So.....the perimeter of the  square = 4 * 10   =   40 units

We can use states to solve the problem: This works out to (e1,e2) = (2,4).

OK.....glad to help    !!!