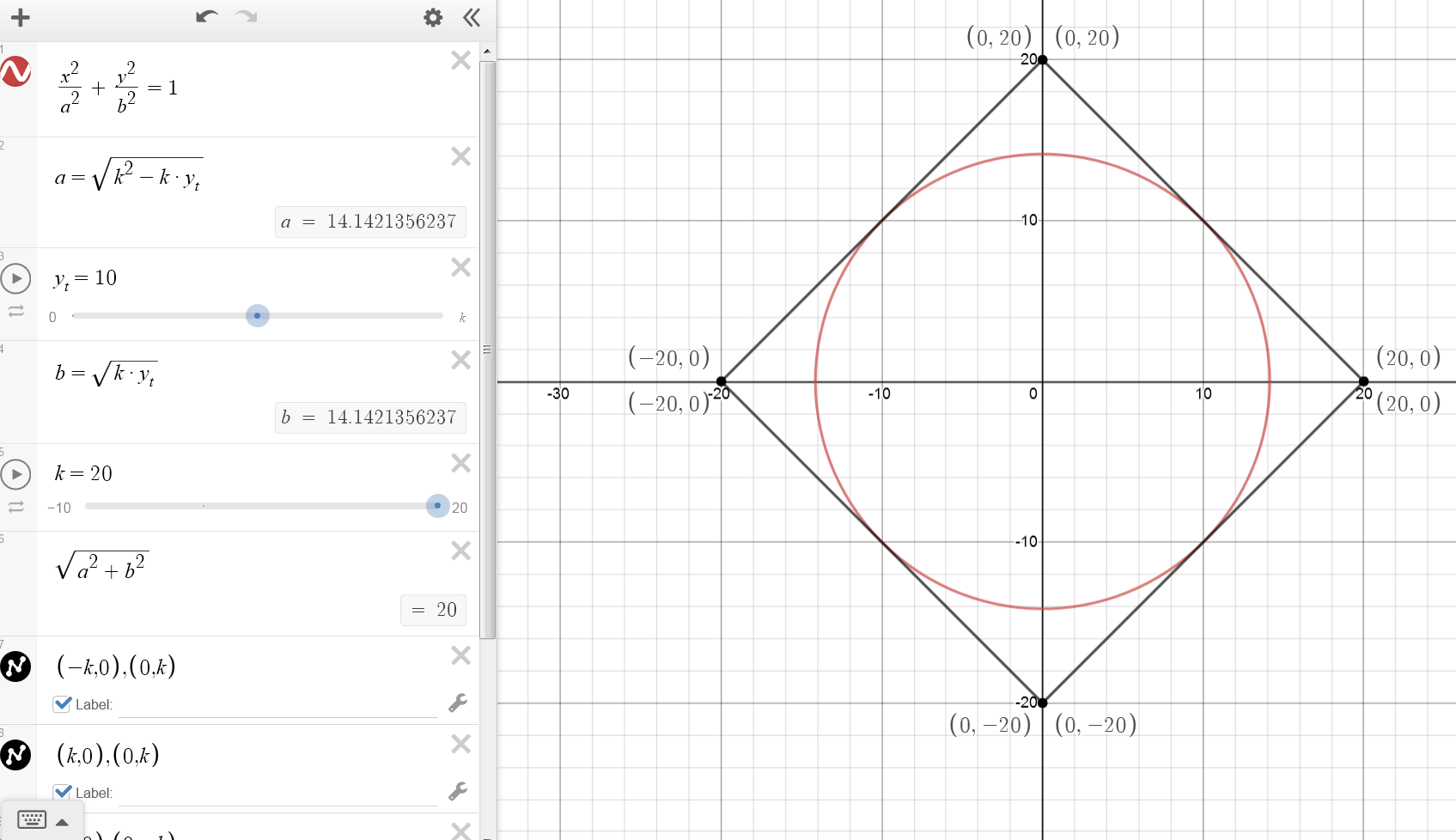
Let k be a positive real number.
The square with vertices \((k, 0)\), \((0,k)\), \((-k,0)\), and \((0,-k)\) is plotted in the coordinate plane.
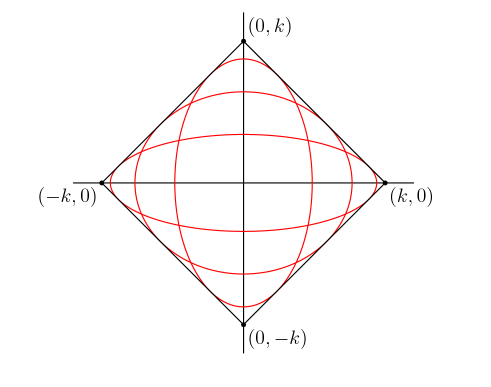
Find conditions on \(a > 0\) and \(b > 0\) such that the ellipse
\(\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1\)
is contained inside the square (and tangent to all its sides).
\(\text{Let $x_t,y_t$ are points on the tangent line $\mathbf{y = x+k}$ from $(-k,0)$ to $(0,k)$, so $ \mathbf{y_t = x_t + k}$}\)
\(\begin{array}{|lrcll|} \hline \text{ellipse} : & \dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} &=& 1 \\ \hline \text{tangent of the ellipse} : & \dfrac{x_tx}{a^2} + \dfrac{y_ty}{b^2} &=& 1 \\ & \dfrac{y_ty}{b^2} &=& 1-\dfrac{x_tx}{a^2} \\ & \ldots \\ & \mathbf{y} &=& \mathbf{\dfrac{b^2}{y_t}-\dfrac{b^2}{a^2}\dfrac{x_t}{y_t}x}\\ &&& \boxed{\text{compare with tangent line }\\ y=k+x} \\ 1. & k &=& \dfrac{b^2}{y_t} \ \text{or}\ \mathbf{b^2} = \mathbf{ky_t} \\\\ 2. & 1 &=& -\dfrac{b^2}{a^2}\dfrac{x_t}{y_t} \quad | \quad \mathbf{b^2} = \mathbf{ky_t} \\\\ & 1 &=& -\dfrac{ky_t}{a^2}\dfrac{x_t}{y_t} \\\\ & 1 &=& -\dfrac{kx_t}{a^2} \\\\ & a^2 &=& -kx_t \quad | \quad x_t = y_t -k \\ & a^2 &=& -k(y_t -k) \\ & a^2 &=& -ky_t +k^2 \\ & \mathbf{a^2} &=& \mathbf{k^2-ky_t} \\ \hline \end{array}\)
\(\begin{array}{|lrcll|} \hline (1): & \mathbf{b^2} &=& \mathbf{ky_t} \\\\ (2): & \mathbf{a^2} &=& \mathbf{k^2-ky_t} \quad | \quad \mathbf{b^2=ky_t} \\ & a^2 &=& k^2-b^2 \\ & \mathbf{a^2+b^2} &=& \mathbf{k^2} \\ & \mathbf{\sqrt{a^2+b^2}} &=& \mathbf{k} \\ \hline \end{array} \)